Bootstrap in R Tutorial

What is a Bootstrap?

Bootstrap is a method of inference about a population using sample data. Bradley Efron first introduced it in this paper in 1979. Bootstrap relies on sampling with replacement from sample data. This technique can be used to estimate the standard error of any statistic and to obtain a confidence interval (CI) for it. Bootstrap is especially useful when CI doesn't have a closed form, or it has a very complicated one.

Suppose we have a sample of n elements: X = {x₁, x₂, …, x_n} and we are interested in CI for some statistic T = t(X). Bootstrap framework is straightforward. We just repeat R times the following scheme: For i-th repetition, sample with replacement n elements from the available sample (some of them will be picked more than once). Call this new sample i-th bootstrap sample, Xi, and calculate desired statistic Ti = t(Xi).

As a result, we'll get R values of our statistic: T₁, T₂, …, T_R. We call them bootstrap realizations of T or a bootstrap distribution of T. Based on it, we can calculate CI for T. There are several ways of doing this. Taking percentiles seems to be the easiest one.

Bootstrap in Action

Let's use (once again) well-known iris dataset. Take a look at a first few rows:

 head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

Suppose we want to find CIs for median Sepal.Length, median Sepal.Width and Spearman's rank correlation coefficient between these two. We'll use R's boot package and a function called... boot. To use its power we have to create a function that calculates our statistic(s) out of resampled data. It should have at least two arguments: a dataset and a vector containing indices of elements from a dataset that were picked to create a bootstrap sample.

If we wish to calculate CIs for more than one statistic at once, our function has to return them as a single vector.

For our example, it may look like this:

 library(boot)

foo <- function(data, indices){
  dt<-data[indices,]
  c(
    cor(dt[,1], dt[,2], method='s'),
    median(dt[,1]),
    median(dt[,2])
  )
}

foo chooses desired elements (which numbers are stored in indices) from data and computes correlation coefficient of first two columns (method='s' is used to choose Spearman's rank coefficient, method='p' will result with Pearson's coefficient) and their medians.

We can also add some extra arguments, eg. let user choose type od correlation coefficient:

 foo <- function(data, indices, cor.type){
  dt<-data[indices,]
  c(
    cor(dt[,1], dt[,2], method=cor.type),
    median(dt[,1]),
    median(dt[,2])
  )
}

To make this tutorial more general, I'll use the latter version of foo.

Now, we can use the boot function. We have to supply it with a name od dataset, function that we've just created, number of repetitions (R) and any additional arguments of our function (like cor.type). Below, I use set.seed for reproducibility of this example.

 set.seed(12345)
myBootstrap <- boot(iris, foo, R=1000, cor.type='s')

boot function returns an object of the class called... (yes, you're right!) boot. It has two interesting elements. $t contains R values of our statistic(s) generated by the bootstrap procedure (bootstrap realizations of T):

 head(myBootstrap$t)

##             [,1] [,2] [,3]
## [1,] -0.26405188 5.70    3
## [2,] -0.12973299 5.80    3
## [3,] -0.07972066 5.75    3
## [4,] -0.16122705 6.00    3
## [5,] -0.20664808 6.00    3
## [6,] -0.12221170 5.80    3

$t0 contains values of our statistic(s) in original, full, dataset:

 myBootstrap$t0

## [1] -0.1667777  5.8000000  3.0000000

Printing boot object to the console gives some further information:

 myBootstrap

##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = iris, statistic = foo, R = 1000, cor.type = "s")
##
##
## Bootstrap Statistics :
##       original       bias    std. error
## t1* -0.1667777  0.002546391  0.07573983
## t2*  5.8000000 -0.013350000  0.10295571
## t3*  3.0000000  0.007900000  0.02726414

original is the same as $t0. bias is a difference between the mean of bootstrap realizations (those from $t), called a bootstrap estimate of T and value in original dataset (the one from $t0).

 colMeans(myBootstrap$t)-myBootstrap$t0

## [1]  0.002546391 -0.013350000  0.007900000

std. error is a standard error of bootstrap estimate, which equals standard deviation of bootstrap realizations.

 apply(myBootstrap$t,2,sd)

## [1] 0.07573983 0.10295571 0.02726414

Different Types of Bootstrap CIs

Before we start with CI, it's always worth to take a look at the distribution of bootstrap realizations. We can use plot function, with index telling at which of statistics computed in foo we wish to look. Here index=1 is a Spearman's correlation coefficient between sepal length and width, index=2 is a median od sepal length, and index=3is a median od sepal width.

plot(myBootstrap, index=1)

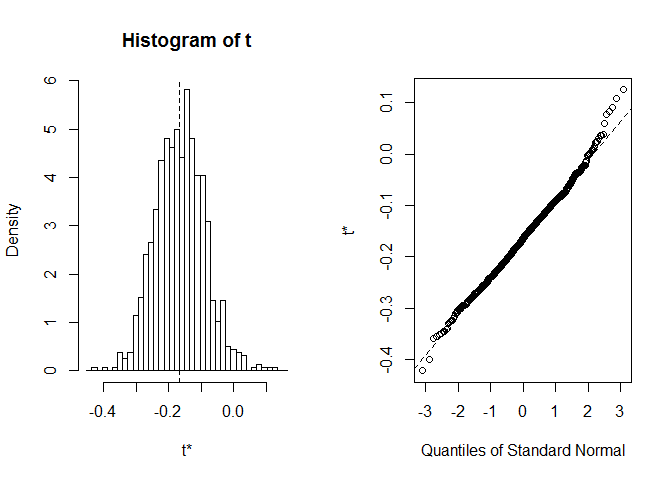
Distribution of bootstrap correlation coefficients seems quite normal-like. Let's find CI for it. We can use boot.ci. It defaults to 95-percent CIs, but it can be changed with the conf parameter.

 boot.ci(myBootstrap, index=1)

## Warning in boot.ci(myBootstrap, index = 1): bootstrap variances needed for
## studentized intervals

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myBootstrap, index = 1)
##
## Intervals :
## Level      Normal              Basic         
## 95%   (-0.3178, -0.0209 )   (-0.3212, -0.0329 )  
##
## Level     Percentile            BCa          
## 95%   (-0.3007, -0.0124 )   (-0.3005, -0.0075 )  
## Calculations and Intervals on Original Scale

boot.ci provides 5 types of bootstrap CIs. One of them, studentized interval, is unique. It needs an estimate of bootstrap variance. We didn't provide it, so R prints a warning: bootstrap variances needed for studentized intervals. Variance estimates can be obtained with second-level bootstrap or (easier) with jackknife technique. This is somehow beyond the scope of this tutorial, so let's focus on the remaining four types of bootstrap CIs.

If we don't want to see them all, we can pick relevant ones in type argument. Possible values are norm, basic, stud, perc, bca or a vector of these.

 boot.ci(myBootstrap, index=1, type=c('basic','perc'))

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myBootstrap, type = c("basic", "perc"), index = 1)
##
## Intervals :
## Level      Basic              Percentile     
## 95%   (-0.3212, -0.0329 )   (-0.3007, -0.0124 )  
## Calculations and Intervals on Original Scale

The boot.ci function creates object of class... (yes, you've guessed!) bootci. Its elements are called just like types of CI used in type argument. $norm is a 3-element vector that contains confidence level and CI bounds.

 boot.ci(myBootstrap, index=1, type='norm')$norm

##      conf                       
## [1,] 0.95 -0.3177714 -0.02087672

$basic, $stud, $perc and $bca are 5-element vectors containing also percentiles used to compute CI (we'll come back to this later):

 boot.ci(myBootstrap, index=1, type='basic')$basic

##      conf                                    
## [1,] 0.95 975.98 25.03 -0.3211981 -0.03285178

A bit of notation (Sorry!)

To get a feeling of what different types of CI are, we need to introduce some notation. So, let:

• t^⋆ be the bootstrap estimate (mean of bootstrap realizations),
• t₀ be a value of our statistic in the original dataset,
• se^⋆ be a standard error of the bootstrap estimate,
• b be a bias of the bootstrap estimate b = t^⋆ − t₀
• α be a confidence level, typically α = 0.95,
• z_α be a $1-\frac \alpha 2$-quantile of standard normal distribution,
• θ_α be an α-percentile of distribution of bootstrap realizations.

Percentile CI

With above notation, percentile CI is:

so this just takes relevant percentiles. Nothing more.

Normal CI

A typical Wald CI would be:

but in bootstrap case, we should correct it for bias. So it becomes:

$$ t_0 - b \pm z_\alpha \cdot se^\star \\ 2t_0 - t^\star \pm z_\alpha \cdot se^\star$$

Basic CI

Percentile CI is generally not recommended because it performs poorly when it comes to weird-tailed distributions. Basic CI (also called pivotal or empirical CI) is much more robust to this. The rationale behind it is to compute differences between each bootstrap replication and t₀ and use percentiles of their distribution. Full details can be found, e.g. in L. Wasserman's All of Statistics

Final formula for basic CI is:

BC_α CI

BC_α comes from bias-corrected, accelerated. The formula for it is not very complicated but somewhat unintuitive, so I'll skip it. See article by Thomas J. DiCiccio and Bradley Efron if you're interested in details.

Acceleration mentioned in method's name requires using specific percentiles of bootstrap realizations. Sometimes it may happen that these would be some extreme percentiles, possibly outliers. BC_α may be unstable in such cases.

Let's look at BC_α CI for petal width median. In original dataset, this median equals precisely 3.

 boot.ci(myBootstrap, index=3)

## Warning in boot.ci(myBootstrap, index = 3): bootstrap variances needed for
## studentized intervals

## Warning in norm.inter(t, adj.alpha): extreme order statistics used as
## endpoints

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = myBootstrap, index = 3)
##
## Intervals :
## Level      Normal              Basic         
## 95%   ( 2.939,  3.046 )   ( 2.900,  3.000 )  
##
## Level     Percentile            BCa          
## 95%   ( 3.0,  3.1 )   ( 2.9,  2.9 )  
## Calculations and Intervals on Original Scale
## Warning : BCa Intervals used Extreme Quantiles
## Some BCa intervals may be unstable

We get BC_α CI (2.9, 2.9). That's weird, but luckily R warned us that extreme order statistics used as endpoints. Let's see what exactly happened here:

 plot(myBootstrap, index=3)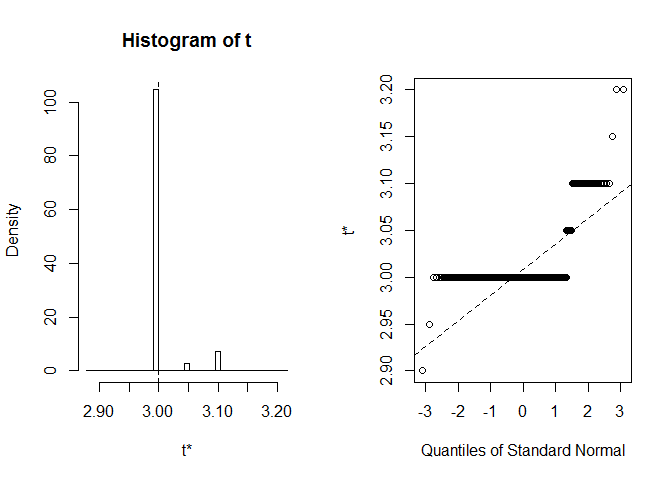

Distribution of bootstrap realizations is unusual. A vast majority of them (over 90%) are 3s.

 table(myBootstrap$t[,3])

##
##  2.9 2.95    3 3.05  3.1 3.15  3.2
##    1    1  908   24   63    1    2

In such a situation, "acceleration" in BC_α method easily "jumps" to extreme values. Here, percentile CI, which forms a basis for BC_α CI is (3, 3.1). Now, when we expand it "to the left" we have to use 0.002-percentile. The expansion "to the right" also goes to extremes: 0.997-percentile.

Replication of Results

Sometimes, we need to recreate bootstrap replications. If we can use R for it, this is not a problem. set.seed function solves the problem. Recreating bootstrap replications in other software would be much more complicated. What is more, for large R, recalculation in R can also not be an option (due to lack of time, for instance).

We can deal with this problem, saving indices of elements of the original dataset, that formed each bootstrap sample. This is what boot.array function (with indices=T argument) does.

 tableOfIndices<-boot.array(myBootstrap, indices=T)

Each row is one bootstrap sample. Eg., our first sample contains the following elements:

 tableOfIndices[1,]

##   [1] 109  12 143  65  41  28 105  62  23 102  37  34  55  53  38   3  11
##  [18] 146  31 122  85 141 118 116 117  78 100  13  98  49  59  88  24  56
##  [35] 136   4  59  67 126 118 104 101  70  13  12  19  21 149  73 133  67
##  [52]  86   6  88 131 105 121 145 121  83  70  68  71 111  76  73 122 116
##  [69]  85 144 114 139  89 124  64  27  81  78  58  39  17  50  37 117  76
##  [86]  97 114  64  17  93 141  65 124  80 137  54  37  57  70 128  10  55
## [103]  13  53  59  45 116  14  77 118 108 138  50  78  49 104  49   1  85
## [120]  28  43  82  74  64  33  55  32  59  62 112   8  11  96  30  14  30
## [137]  38  85  66  85  97 107   4  18  76  35  31 133  27  69

Setting indices=F (a default), we'll get an answer to the question "How many times each element of original dataset appeared in each bootstrap sample?". For example, in the first sample: the 1st element of dataset appeared once, 2nd element didn't appear at all, 3rd element appeared once, 4th twice and so on.

 tableOfAppearances<-boot.array(myBootstrap)
tableOfAppearances[1,]

##   [1] 1 0 1 2 0 1 0 1 0 1 2 2 3 2 0 0 2 1 1 0 1 0 1 1 0 0 2 2 0 2 2 1 1 1 1
##  [36] 0 3 2 1 0 1 0 1 0 1 0 0 0 3 2 0 0 2 1 3 1 1 1 4 0 0 2 0 3 2 1 2 1 1 3
##  [71] 1 0 2 1 0 3 1 3 0 1 1 1 1 0 5 1 0 2 1 0 0 0 1 0 0 1 2 1 0 1 1 1 0 2 2
## [106] 0 1 1 1 0 1 1 0 2 0 3 2 3 0 0 2 2 0 2 0 1 0 1 0 0 1 0 2 0 0 1 1 1 1 0
## [141] 2 0 1 1 1 1 0 0 1 0

A table like this allows us to recreate bootstrap realization outside R. Or in R itself when we don't want to use set.seed and do all the computation once again.

 onceAgain<-apply(tableOfIndices, 1, foo, data=iris, cor.type='s')

Let's check if results are the same:

 head(t(onceAgain))

##             [,1] [,2] [,3]
## [1,] -0.26405188 5.70    3
## [2,] -0.12973299 5.80    3
## [3,] -0.07972066 5.75    3
## [4,] -0.16122705 6.00    3
## [5,] -0.20664808 6.00    3
## [6,] -0.12221170 5.80    3

head(myBootstrap$t)

##             [,1] [,2] [,3]
## [1,] -0.26405188 5.70    3
## [2,] -0.12973299 5.80    3
## [3,] -0.07972066 5.75    3
## [4,] -0.16122705 6.00    3
## [5,] -0.20664808 6.00    3
## [6,] -0.12221170 5.80    3

all(t(onceAgain)==myBootstrap$t)

## [1] TRUE

Yes, they are!

If you would like to learn more about Machine Learning in R, take DataCamp's Machine Learning Toolbox course and check out the Machine Learning in R for beginners tutorial.