Course
When you think of it, many functions in R make use of formulas: packages such as ggplot2, stats, lattice, and dplyr all use them! Common examples of functions where you will use these R objects are glm(), lm(), facet_wrap(), etc. But what exactly are these formulas, and why should you use them?
Data Structures in R
Since formulas are a special class in the R programming language, it's a good idea to briefly revise the data types and data structures that you have available in this programming language.
Remember R is an object-oriented programming language: this language is organized around objects. Everything in R is an object.
Let's start at the beginning: in programming, you work with data structures store your data, and functions process it. A data structure is the interface to data organized in computer memory. As the R Language Definition states, R does not provide direct access to the computer’s memory but rather provides a number of specialized data structures that you can refer to as "objects". Data structures are each designed to optimize some aspect of storage, access, or processing.
The five main data structures in R are:
- Atomic vector,
- List,
- Matrix,
- Data frame, and
- Array
# Create variables
a <- c(1,2,3,4,5,6,7,8,9)
b <- list(x = LifeCycleSavings[,1], y = LifeCycleSavings[,2])
Tip: you can use the typeof() function to return the type of an R object. The type of an object tells you more about the (R internal) type or storage mode of any object:
# Retrieve the types of `a` and `b`
typeof(a)
typeof(b)
'double'
'list'
In the above example where you defined the variables a and b, you can see that the data structures contain sequences of data elements. These elements can be of the same or different data types. You can find the following 6 atomic data types in R:
- numeric, such as
100,5,4, includes integers. - character, such as
"Hello","True", or"23.4", consists of strings of keyboard characters.; - logical, such as
TRUEorFALSE, consists of "truth values"; - raw, such as
48 65 6c 6c 6f, consists of bits; - complex, such as
2+5i, includes complex numbers; And, lastly, - double, such as
3.14, includes decimal numbers.
Almost all objects have attributes attached to them in R. For example, you might already know that matrices and arrays are simply vectors with the attribute dim and optionally dimnames attached to the vector. Attributes are used to implement the class structure used in R. As an object-oriented programming language, the concept of classes, together with methods, is central to it. A class is a definition of an object. It defines what information the object contains and how that object can be used.
Check out the following example:
# Retrieve the classes of `a` and `b`
class(a)
class(b)
'numeric'
'list'
Note that if an object does not have a class attribute, it has an implicit class, "matrix", "array" or the result of the mode() function.
Some of the special classes that you can encounter are Dates and Formulas; And this last one is the topic of today's tutorial!
What is a Formula in R?
As you read in the introduction of this tutorial, you might have already seen formulas appear when working with packages such as ggplot2 or in functions such as lm(). Since you usually use formulas inside these function calls to express the idea of a statistical model, it's only logical that you often use these R objects in modeling functions as well as in some graphical functions.
Right?
However, formulas aren't limited to models. They are a powerful, general-purpose tool that allows you to capture two things:
- An unevaluated expression, and
- The context or environment in which the expression was created.
This explains why formulas are used inside function calls to generate "special behavior": they allow you to capture the values of variables without evaluating them so that they can be interpreted by the function.
With the data structures fresh in mind, you can then describe these R objects as “language” objects or unevaluated expressions that have a class of “formula” and an attribute that stores the environment.
In the previous section, you saw that objects have certain (R internal) types that indicate how the object was stored. In this case, a formula is an object of type "language".
But what does that exactly mean?
Well, you usually come across this type of objects when you're processing the R language itself. Take a look at the following example to understand this better:
# Retrieve the object type
typeof(quote(x * 10))
# Retrieve the class
class(quote(x * 10))
'language'
'call'
In the example above, you ask R to return the type and the class of quote(x*10). As a result, you see that the type of quote(x*10) is 'language', and the class is 'call'.
This is definitely not a formula, since you would need the class() to return 'formula'!
But what then is?
Something that characterizes formulas in R is the tilde operator ~. With this operator, you can actually say: "capture the meaning of this code, without evaluating it right away”. That also explains why you can think of a formula in R as a "quoting" operator.
But what does a formula exactly look like? Take a closer look at the following line of code:
# A formula
c <- y ~ x
d <- y ~ x + b
# Double check the class of `c`
class(c)
'formula'
The variable on the left-hand side of a tilde (~) is called the "dependent variable", while the variables on the right-hand side are called the "independent variables" and are joined by plus signs +.
It's good to know that the names for these variables change depending on the context. You might have already seen independent variables appear as "predictor (variable)", "controlled variable", "feature", etc. Similarly, you might come across dependent variables as "response variable", "outcome variable" or "label".
Note that, even though the formula d that you defined in the code chunk above contains a couple of variables, the basic structure of a formula is actually just the tilde symbol ~ and at least one independent or right-hand variable.
Remember that formulas are actually language objects with attributes that store the environment:
# Return the type of `d`
typeof(d)
# Retrieve the attributes of `d`
attributes(d)
'language'
$class
[1] "formula"
$.Environment
<environment: R_GlobalEnv>
As you saw in the examples above, the variables that are included in a formula can be vectors, for example. However, you'll often see that the variables that are included in formulas come from a data frame, just like in the following example:
Sepal.Width ~ Petal.Width + log(Petal.Length) + Species
Note that any data values that have been assigned to the symbols in the formula are not accessed when the formula itself is created.
Now that you know what formulas look like and what they are in R, it's good to mention that the underlying formula object varies, depending on whether you have a one-sided or two-sided formula. You can recognize the former by looking at the left-hand side variable. If there is none, just like in ~ x, you have a one-sided formula.
This also means that a one-sided formula will have a length of 2, while the two-sided formula will have a length of 3.
Not totally convinced? Take a look at the following code chunk. You can access the elements of a formula with the help of the square brackets: [[and ]].
e <- ~ x + y + z
f <- y ~ x + b
# Return the length of `g`
length(e)
length(f)
# Retrieve the elements at index 1 and 2
e[[1]]
e[[2]]
f[[3]]
2
3
`~`
x + y + z
x + bWhy Use Formulae in R?
As you have seen, formulas powerful, general-purpose tools that allow you to capture the values of variables without evaluating them so that they can be interpreted by the function. That's already one part of the answer on why you should use formulas in R.
Also, you use these R objects to express a relationship between variables.
For example, in the first line of code in the code chunk below, you say "y is a function of x, a, and b" with the first line of code; Of course, you can also come across more complex formulas, such as in the second line of code, where you mean to say "the sepal width is a function of petal width, conditioned on species".
y ~ x + a + b
Sepal.Width ~ Petal.Width | Species
y ~ x + a + b
Sepal.Width ~ Petal.Width | SpeciesUsing Formulas in R
Now that you know more about the "what" and the "why" of these special R objects, it's time to learn about how you can use basic as well as more complex formulas! In this section, you'll not only see how you can create and concatenate basic formulas, but you'll also discover how you can build more complex ones with the help of operators.
How to Create a Formula in R
You already know how to do this! You have already seen some examples in this tutorial, but let's recapitulate:
y ~ x
~ x + y + z
g <- y ~ x + b
That's right - You can just type the formula!
However, you'll probably find yourself in a situation where you need or want to create a formula from an R object, such as a string. In such cases, you can use the formula or as.formula() function:
"y ~ x1 + x2"
h <- as.formula("y ~ x1 + x2")
h <- formula("y ~ x1 + x2")
Easy!
How to Concatenate Formulae
To glue or bring multiple formulas together, you have two options. Firstly, you can create separate variables for each formula and then use list():
# Create variables
i <- y ~ x
j <- y ~ x + x1
k <- y ~ x + x1 + x2
# Concatentate
formulae <- list(as.formula(i),as.formula(j),as.formula(k))
# Double check the class of the list elements
class(formulae[[1]])
'formula'
Alternatively, you can also use the lapply() function, where you pass in a vector with all of your formulas as a first argument and as.formula as the function that you want to apply to each element of that vector:
# Join all with `c()`
l <- c(i, j, k)
# Apply `as.formula` to all elements of `f`
lapply(l, as.formula)
[[1]]
y ~ x
[[2]]
y ~ x + x1
[[3]]
y ~ x + x1 + x2
Formula Operators
With these basics in mind, you're ready to deep dive into some more complex formulas! In the above, you have already seen that what characterizes formulae is the tilde symbol ~. In addition to that symbol, you have seen that you also need dependent and independent variables and that these can be joined with the plus sign +.
But there is more!
In addition to the + symbol, there are also other symbols that can add special meaning to your formulas:
-for removing terms;:for interaction;*for crossing;%in%for nesting; And^for limit crossing to the specified degree.
You'll see examples of all of these operators in the rest of this section! Let's first start off with the + and - operators:
# Use multiple independent variables
y ~ x1 + x2
# Ignore objects in an analysis
y ~ x1 - x2
Note that you'll most often need the :and * symbols in a regression modeling context, where you need to specify interaction terms. As you have read above, the former symbol is used for interaction, which means that you only want the variables' interaction, and not the variables themselves. This stands in contrast with the latter symbol, which is used for crossing: you use it to include two variables and their interaction.
Be careful! By using these operators, some formulae can look different but will actually be equivalent. Consider the following examples, which will produce the same regression:
y ~ x1 * x2
y ~ x1 + x2 + x1:x2
Not sure how these two can be the same? Consider the following R code chunks:
# Set seed
set.seed(123)
# Data
x = rnorm(5)
x2 = rnorm(5)
y = rnorm(5)
# Model frame
model.frame(y ~ x * x2, data = data.frame(x = x, y = y, x2=x2))
| y | x | x2 |
|---|---|---|
| 1.7150650 | -0.56047565 | 1.2240818 |
| 0.4609162 | -0.23017749 | 0.3598138 |
| -1.2650612 | 1.55870831 | 0.4007715 |
| -0.6868529 | 0.07050839 | 0.1106827 |
| -0.4456620 | 0.12928774 | -0.5558411 |
model.frame(y ~ x + x2 + x:x2, data = data.frame(x = x, y = y, x2))
| y | x | x2 |
|---|---|---|
| 1.7150650 | -0.56047565 | 1.2240818 |
| 0.4609162 | -0.23017749 | 0.3598138 |
| -1.2650612 | 1.55870831 | 0.4007715 |
| -0.6868529 | 0.07050839 | 0.1106827 |
| -0.4456620 | 0.12928774 | -0.5558411 |
Don't worry if you don't know the model.frame() function yet; You'll see more on this later on in this tutorial!
In addition, here's an example of nesting, which you can expand to y ~ a + a:b:
y ~ a + b %in% a
All these operators are really cool, but what if you want to actually perform an arithmetic operation? Let's say you want to include x and x^2 in your model. In such cases, you might feel tempted to write the following formula: y ~ x + x^2.
But will the result be exactly what you want? Take a look!
model.frame( y ~ x + x^2, data = data.frame(x = rnorm(5), y = rnorm(5)))
y ~ x + x^2
| y | x |
|---|---|
| -0.2053091 | 1.18231565 |
| -0.3030972 | 0.04779636 |
| -0.7621604 | 0.86382418 |
| -0.1377784 | -1.18333097 |
| -0.3813125 | -1.25247842 |
That's not the result that you were expecting!
In the above example, you don't protect the arithmetic expression and as a consequence, R would drop x^2 term, as it is considered a duplicate of x.
Why is this?
Well, x would give you the main effect of x, and x^2 would give you the main effect and the second order interaction of x. In the end, you will end up including x in the model frame because the main effect of x is already included from the x term in the formula, and there is nothing to cross x with to get the second-order interactions in the x^2 term.
To avoid this, you have a couple of solutions:
- You can calculate and store all of the variables in advance
- You use the
I()or "as-is" operator:y ~ x + I(x^2)
Take a look at the following example to understand the consequences of adding the I() function to your code:
model.frame( y ~ x + I(x^2), data = data.frame(x = rnorm(5), y = rnorm(5)))
y ~ x + I(x^2)| y | x | I(x^2) |
|---|---|---|
| 1.414090 | -0.1996230 | 0.039849.... |
| 1.777646 | -1.0675904 | 1.139749.... |
| 1.710137 | -1.4071841 | 1.980167.... |
| 1.259111 | -1.3747289 | 1.889879.... |
| -1.490866 | 0.8323668 | 0.692834.... |
This last line of code actually tells R to calculate the values of x^2 before using the formula. Note also that you can use the "as-is" operator to escale a variable for a model; You just have to wrap the relevant variable name in I():
y ~ I(2 * x)
This might all seem quite abstract when you see the above examples, so let's cover some other cases; For example, take the polynomial regression. In such cases, you'll need to work with the I() function. For a factorial ANOVA model that is limited to depth=2 interactions, on the other hand, you won't need this function because you want to expand to a formula that contains the main effects for a, b and c together with their second-order interactions:
# Polynomial Regression
y ~ x + I(x^2) + I(x^3)
# Factorial ANOVA
y ~ (a*b*c)^2
Lastly, there is one other feature that you'll find helpful when you're working with multiple variables and that's the . operator. When you use this operator within a formula, you refer to all other variables in the matrix that haven't yet been included in the model. This is handy, for example, when you want to run a regression on a matrix or dataframe and you don't want to type all of the variables:
y ~ .
How to Inspect Formulas in R
When you have created a formula, you might also want to inspect it. In this section, you'll get introduced to some of the tools that you can use to further explore the special R objects you created!
Note that you have already seen some ways in which you can examine formulas in the previous sections: you saw functions such as attributes(), typeof(), class(), etc.
terms() function
To examine and compare different formulae, you can use the terms() function:
m <- formula("y ~ x1 + x2")
terms(m)
y ~ x1 + x2
attr(,"variables")
list(y, x1, x2)
attr(,"factors")
x1 x2
y 0 0
x1 1 0
x2 0 1
attr(,"term.labels")
[1] "x1" "x2"
attr(,"order")
[1] 1 1
attr(,"intercept")
[1] 1
attr(,"response")
[1] 1
attr(,".Environment")
<environment: R_GlobalEnv>all.vars
If you want to know the names of the variables in the model, you can use all.vars. With this function, you return a character vector that contains all the names which occur in a formula:
print(all.vars(m))
[1] "y" "x1" "x2"update() function
To modify formulae without converting them to character you can use the update() function:
update(y ~ x1 + x2, ~. + x3)
y ~ x1 + x2 + x3
Note that you could have also updated the formula by converting it to character with as.character(); Then, you can build formulae very quickly by using paste(). For example, if you want to add another right-hand variable to your formula, you can simply paste it:
as.formula(paste("y ~ x1 + x2", "x3", sep = "+"))
factors <- c("x2", "x3")
as.formula(paste("y~", paste(factors, collapse="+")))
y ~ x1 + x2 + x3
y ~ x2 + x3
In the above code chunk, you can see that you can either make use of the sep or the collapse arguments to indicate a character string to separate the terms within your formula.
However, using paste() is definitely not the only way to make adjustments to your formula: you can also use reformulate():
reformulate(termlabels = factors, response = 'y')
y ~ x2 + x3
is.formula()
Double check whether you variable is a formula by passing it to the is.formula() function. Take into account that this function is part the plyr library, so you'll need to make that one available in your workspace before you call is.formula()!
# Load `plyr`
library(plyr)
# Check `m`
is.formula(m)
TRUE
When to Use Formulas
Up until now, you have already read that the R formulas are general-purpose tools that aren't limited to modeling and you have seen some examples where you can use formulas. In this section, you'll go deeper into this last topic: you'll get to see some cases where you can use these tools to your advantage. Of course, you'll cover modeling- and graphical functions of packages such as lattice and stats, but you'll also cover non-standard evaluation in dplyr.
Modeling Functions
R is great for when you need to do statistical modeling. As you already know, statistical modeling is a simplified, mathematically-formalized way to approximate reality and optionally to make predictions from this approximation. A statistical model often represents the data generating process in an idealized form. To do statistical modeling, you need modeling functions.
The modeling functions in R are one typical example where you need a formula object as an argument. Other arguments that you might find in these functions are data, which allows you to specify a data frame that you want to attach for the duration of the model, subset to select the data that you want to use, ... In general, if you would like to know which arguments to pass to any specific function, don't hestitate to use the help() function or ? in your R console.
The modeling functions return a model object that contains all the information about the fit. Generic R functions such as print(), summary(), plot(), anova(), etc. will have methods defined for specific object classes to return information that is appropriate for that kind of object.
Probably one of the well known modeling functions is lm(), which uses all of the arguments described above. You use lm() to fit linear models. You can use it to perform regression, single stratum analysis of variance and analysis of covariance. Let's take a look at an example where you use lm() and inspect the model with the help of print():
lm.m <- lm(Sepal.Width ~ Petal.Width + log(Petal.Length) + Species,
data = iris,
subset = Sepal.Length > 4.6)
print(lm.m)
Call:
lm(formula = Sepal.Width ~ Petal.Width + log(Petal.Length) +
Species, data = iris, subset = Sepal.Length > 4.6)
Coefficients:
(Intercept) Petal.Width log(Petal.Length) Speciesversicolor
3.1531 0.6620 0.4612 -1.9265
Speciesvirginica
-2.3088 lm() initially uses the formula and the appropriate environment to translate the relationships between variables to creating a data frame containing the data.
There's also the model.frame() methods, of which you already saw one example in this tutorial, that are most often used to retrieve or recreate the model frame from the fitted object, with no other arguments. This allows you to retrieve columns of the data frame that correspond to arguments of the orginal call other than formula, subset and weights: for example, the glm() method handles offset, etastart and mustart.
In the following code chunk, you see that you use the model.frame() function to get back a data frame of the fitted object; Note that the code is slightly different from the code chunk that you saw above: the subset argument has been modified slightly.
stats::model.frame(formula = Sepal.Width ~ Petal.Width + log(Petal.Length) + Species,
data = iris,
subset = Sepal.Length > 6.9,
drop.unused.levels = TRUE)
| Sepal.Width | Petal.Width | log(Petal.Length) | Species | |
|---|---|---|---|---|
| 51 | 3.2 | 1.4 | 1.547563 | versicolor |
| 103 | 3.0 | 2.1 | 1.774952 | virginica |
| 106 | 3.0 | 2.1 | 1.887070 | virginica |
| 108 | 2.9 | 1.8 | 1.840550 | virginica |
| 110 | 3.6 | 2.5 | 1.808289 | virginica |
| 118 | 3.8 | 2.2 | 1.902108 | virginica |
| 119 | 2.6 | 2.3 | 1.931521 | virginica |
| 123 | 2.8 | 2.0 | 1.902108 | virginica |
| 126 | 3.2 | 1.8 | 1.791759 | virginica |
| 130 | 3.0 | 1.6 | 1.757858 | virginica |
| 131 | 2.8 | 1.9 | 1.808289 | virginica |
| 132 | 3.8 | 2.0 | 1.856298 | virginica |
| 136 | 3.0 | 2.3 | 1.808289 | virginica |
Tip: there are even more functions in the stats package that allow you to use formulas, such as aggregate().
For linear mixed-effects models, which allow you to model random effects to account for variation that are the result of factors such as observer differences, you can use the nlme package with the lme() function. Also here, you see that formula is the first argument that you need to provide to the modeling function, and there is also a data argument!
# Load packages
library(MASS)
library(nlme)
# Get some data
data(oats)
# Adjust the data names and columns
names(oats) = c('block', 'variety', 'nitrogen', 'yield')
oats$mainplot = oats$variety
oats$subplot = oats$nitrogen
# Fit a non-linear mixed-effects model
nlme.m = lme(yield ~ variety*nitrogen,
random = ~ 1|block/mainplot,
data = oats)
# Retrieve a summary
summary(nlme.m)
Linear mixed-effects model fit by REML
Data: oats
AIC BIC logLik
559.0285 590.4437 -264.5143
Random effects:
Formula: ~1 | block
(Intercept)
StdDev: 14.64496
Formula: ~1 | mainplot %in% block
(Intercept) Residual
StdDev: 10.29863 13.30727
Fixed effects: yield ~ variety * nitrogen
Value Std.Error DF t-value p-value
(Intercept) 80.00000 9.106958 45 8.784492 0.0000
varietyMarvellous 6.66667 9.715028 10 0.686222 0.5082
varietyVictory -8.50000 9.715028 10 -0.874933 0.4021
nitrogen0.2cwt 18.50000 7.682957 45 2.407927 0.0202
nitrogen0.4cwt 34.66667 7.682957 45 4.512152 0.0000
nitrogen0.6cwt 44.83333 7.682957 45 5.835427 0.0000
varietyMarvellous:nitrogen0.2cwt 3.33333 10.865342 45 0.306786 0.7604
varietyVictory:nitrogen0.2cwt -0.33333 10.865342 45 -0.030679 0.9757
varietyMarvellous:nitrogen0.4cwt -4.16667 10.865342 45 -0.383482 0.7032
varietyVictory:nitrogen0.4cwt 4.66667 10.865342 45 0.429500 0.6696
varietyMarvellous:nitrogen0.6cwt -4.66667 10.865342 45 -0.429500 0.6696
varietyVictory:nitrogen0.6cwt 2.16667 10.865342 45 0.199411 0.8428
Correlation:
(Intr) vrtyMr vrtyVc ntr0.2 ntr0.4 ntr0.6
varietyMarvellous -0.533
varietyVictory -0.533 0.500
nitrogen0.2cwt -0.422 0.395 0.395
nitrogen0.4cwt -0.422 0.395 0.395 0.500
nitrogen0.6cwt -0.422 0.395 0.395 0.500 0.500
varietyMarvellous:nitrogen0.2cwt 0.298 -0.559 -0.280 -0.707 -0.354 -0.354
varietyVictory:nitrogen0.2cwt 0.298 -0.280 -0.559 -0.707 -0.354 -0.354
varietyMarvellous:nitrogen0.4cwt 0.298 -0.559 -0.280 -0.354 -0.707 -0.354
varietyVictory:nitrogen0.4cwt 0.298 -0.280 -0.559 -0.354 -0.707 -0.354
varietyMarvellous:nitrogen0.6cwt 0.298 -0.559 -0.280 -0.354 -0.354 -0.707
varietyVictory:nitrogen0.6cwt 0.298 -0.280 -0.559 -0.354 -0.354 -0.707
vM:0.2 vV:0.2 vM:0.4 vV:0.4 vM:0.6
varietyMarvellous
varietyVictory
nitrogen0.2cwt
nitrogen0.4cwt
nitrogen0.6cwt
varietyMarvellous:nitrogen0.2cwt
varietyVictory:nitrogen0.2cwt 0.500
varietyMarvellous:nitrogen0.4cwt 0.500 0.250
varietyVictory:nitrogen0.4cwt 0.250 0.500 0.500
varietyMarvellous:nitrogen0.6cwt 0.500 0.250 0.500 0.250
varietyVictory:nitrogen0.6cwt 0.250 0.500 0.250 0.500 0.500
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-1.81300898 -0.56144838 0.01758044 0.63864476 1.57034166
Number of Observations: 72
Number of Groups:
block mainplot %in% block
6 18 Note that besides nlme, there are also other packages, such as the lme4 package, which is also dedicated to fitting linear and generalized linear mixed-effects models.
Another example of modeling functions and the presence of formulas is nls(), which you would use to make non-linear models:
# Set seed
set.seed(20160227)
# Data
x <- seq(0,50,1)
y <- ((runif(1,10,20)*x)/(runif(1,0,10)+x))+rnorm(51,0,1)
# Non-linear model
nls.m <- nls(y ~ a*x/(b+x),
start=c(a=4, b=1))
A last example are functions that you can use to build Generalized Linear Models (GLM). In R, you can make use of the glm() function to do this. It's probably getting a bit old, but also here you make use of the formula and data arguments:
# Load package
library(MPDiR)
# Get the data
data(Chromatic)
# Model
glm.m <- glm(Thresh ~ Axis:(I(Age^-1) + Age),
family = Gamma(link = "identity"),
data = Chromatic)
# Get back a summary
summary(glm.m)
Call:
glm(formula = Thresh ~ Axis:(I(Age^-1) + Age), family = Gamma(link = "identity"),
data = Chromatic)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.2160 -0.3728 -0.0805 0.2311 1.2932
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.282e-04 9.965e-05 3.294 0.00106 **
AxisDeutan:I(Age^-1) 7.803e-03 3.686e-04 21.172 < 2e-16 ***
AxisProtan:I(Age^-1) 8.271e-03 3.863e-04 21.410 < 2e-16 ***
AxisTritan:I(Age^-1) 1.166e-02 5.284e-04 22.065 < 2e-16 ***
AxisDeutan:Age 1.521e-05 3.418e-06 4.450 1.06e-05 ***
AxisProtan:Age 1.540e-05 3.434e-06 4.484 9.10e-06 ***
AxisTritan:Age 4.812e-05 5.838e-06 8.241 1.48e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Gamma family taken to be 0.2054848)
Null deviance: 543.35 on 510 degrees of freedom
Residual deviance: 100.40 on 504 degrees of freedom
AIC: -4777.6
Number of Fisher Scoring iterations: 6Before you pass on to the graphical functions, there's one more thing that is good to know: when you use formulas in modeling functions such as lm(), a standard conversion takes place from formula to functions. To explain what type of conversion exactly takes place, you should return to the example that you saw earlier in this tutorial:
lm.m <- lm(Sepal.Width ~ Petal.Width + log(Petal.Length) + Species,
data = iris,
subset = Sepal.Length > 4.6)
While the purpose of this code chunk is to fit a linear regression models, the formula is used to specify the symbolic model as well as generating the intended design matrix. A design matrix is the two-dimensional representation of the predictor or the independent variable set where instances of data are in rows and variable attributes are in columns. The design matrix is also known as the X matrix.
That being said, the formula method also defines the columns that should be included in the design matrix.
But what exactly does all of that mean? Let's take a look at the following lines of code:
# A formula
y ~ x
# A converted formula
y = a_1 + a_2 * x
This is an example of a simple conversion: y ~ x gets translated into y = a_1 + a_2 * x.
To see and understand what R actually happens, you can use the model_matrix() function. This function creates a design or model matrix by, for example, expanding factors to a set of dummy variables, depending on the contrasts, and expanding interactions similarly.
Don't forget to pass in the data frame dfand the formula to get back a tibble that defines the model equation:
# Load packages
library(tidyverse)
library(modelr)
# A data frame
df <- tribble(
~y, ~x1, ~x2,
4, 2, 5,
5, 1, 6
)
# Model matrix
model_matrix(df, y ~ x1)
| (Intercept) | x1 |
|---|---|
| 1 | 2 |
| 1 | 1 |
There's an extra (Intercept) column that appears. This is default behavior on R's side. However, the way that R adds the intercept to the model is just by having a column that is full of ones. If you don’t want this, you need to explicitly drop it by adding -1 to the formula, just like this:
model_matrix(df, y ~ x1-1)
| x1 |
|---|
| 2 |
| 1 |
Note also that the model matrix grows in an unsurprising way when you add more variables to the the model.
model_matrix(df, y ~ x1 + x2)
| (Intercept) | x1 | x2 |
|---|---|---|
| 1 | 2 | 5 |
| 1 | 1 | 6 |
Graphical Functions in R
Another important place where you'll find formulae in R are the graphical functions. There are a whole bunch of packages out there, so this tutorial will only focus on graphics, lattice, ggplot2 and ggformula.
graphics
The base R package graphics allows you to specify a scatterplot or add points, lines, or text using a formula. Take a look at the following example:
# Get data
data(airquality)
# Plot
plot(Ozone ~ Wind, data = airquality, pch = as.character(Month))
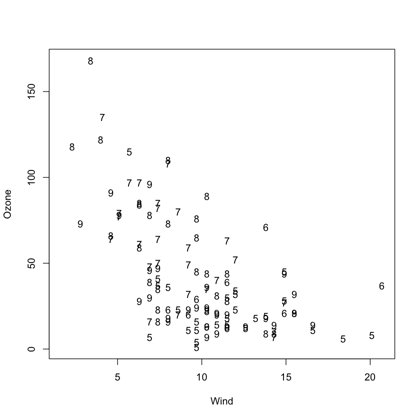
If you want to know more, don't hesitate to check out this page.
lattice
lattice is a package that is built on grid graphics. It's a general-purpose graphics package that provides alternative implementations of many of the plotting functions available in base graphics. Specific examples include scatterplots with the xyplot() function, bar charts with the barchart() function, and boxplots with the bwplot() function.
Tip: do you want to learn more about lattice? Consider taking DataCamp's Data Visualization in R with lattice course.
What's so special about this package is that it uses the formula notation of statistical models to describe the desired plot, and more specifically, the variables to plot. It also adds the pipe character or vertical bar | to specify the conditioning variable:
# Load package
library(lattice)
# Plot histogram
histogram(~ Ozone | factor(Month),
data = airquality,
layout = c(2, 3),
xlab = "Ozone (ppb)")
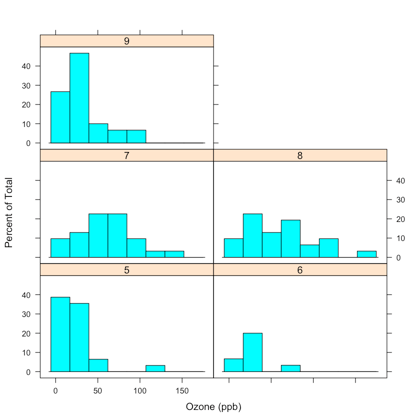
Note that just like the modeling functions, the functions in the lattice library have, besides a formula argument, also a data argument, just like one would expect!
Remember that you could also omit the data argument in the code chunk above, but then you would need to attach the data:
# Load package
library(lattice)
# Attach data
attach(airquality)
# Plot
histogram(~ Ozone | factor(Month),
layout = c(2, 3),
xlab = "Ozone (ppb)")
ggplot2
You can use formulas in various ggplot2 functions:
geom_smooth()orstats_smooth(), to specify the formula to use in the smoothing function; This will influence the form of the fit.facet_wrap(), to specify panels for plotting.facet_grid(), to specify the rows and columns that needs to be plotted, with or without faceting.
# Load package
library(ggplot2)
# Plot
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
geom_smooth(method = "lm",
formula = y ~ splines::bs(x, 3),
se = FALSE)
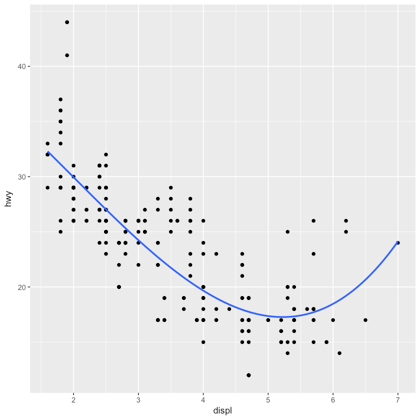
Note that, to create this plot, the formula uses the letters x and y, not the names of the variables. This is not so when you use facet_wrap():
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
geom_smooth(span = 0.8) +
facet_wrap(~drv)
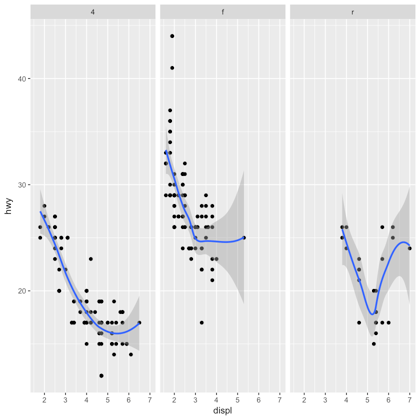
Want to learn more about ggplot2? Take a look at this course or check out the documentation.
ggformula
The ggformula package currently builds on ggplot2, but provides an interface that is based on formulas. This is similar to what you find in the lattice interface. You'll also find that the pipe operator is used in this package to build more complex graphics from simpeler components.
Tip: if you want to know more about the pipe operator in R, consider this tutorial.
The basic way of creating a plot with ggformula is
gf_plottype(formula, data = mydata)Note that the function gf_plottype() actually starts with gf, which is to remind you that you're working with functions that are formula-based interfaces to ggplot2; The g stands for for ggplot2 and f for “formula.”
Take a look at the following example to see what this looks like in R code:
# Load package
library(ggformula)
# Plot
gf_point(mpg ~ hp, data = mtcars)

Of course, this is just a basic graph; You can do much more with this visualization package! You can select a different glyph type and specific attributes for those glyphs, you can make one- or 2 variable plots, adjust the positions of the glyphs, and so on. This tutorial won't go into much more detail on this package, but the main take-away here is that this package has made formulas the main ingredient for making graphs!
If you do want to know more than what you have covered in this tutorial, read about the ggformula package here or consult the RDocumentation page on the package.
dplyr
dplyr is an example of a package that works with Non-Standard Evaluation. Other examples are library(magrittr) versus library("magrittr"), which both work perfectly, even though there are quotations in one line and not in the other! Compare these examples of library() with install.packages(), for example:
# This will work
install.packages("magrittr")
# This won't work
install.packages(magrittr)
In R, you usually need to use the quotes whenever you're naming a part of an object, but in some functions -like library()- you don't. These functions are designed to work in a non-standard way. What's more, some of these functions even miss a standard way!
For what concerns dplyr, you'll find that most functions of this package work just like other functions: all functions use Standard Evaluation (SE). However, for interactive use, functions also have a Non-Standard Evaluation (NSE), which saves you some typing.
(Let's face it, typing all of those quotes can be a daunting task!)
That's why most dplyr functions use non-standard evaluation. They don’t follow the usual R rules of evaluation. Instead, they capture the expression that you typed and evaluate it in a custom way.
That, however, doesn't mean that these functions don't have a standard evaluation variant. Every function that uses non-standard evaluation has (and should have) a standard evaluation escape hash that does the actual computation. The standard-evaluation function should end with _. This then means that there are multiple verbs in the dplyr package: select(), select_(), mutate(), mutate_(), etc.
When used interactively, these functions will first be evaluated with the lazyeval package before they get sent to the standard evaluation version of the function. That means that, uder the hood, select() is evaluated with the lazyeval package and send to select_().
That all being said, there are 3 ways to quote variables in standard evaluation functions that dplyr and lazyeval understand:
- Formulas,
quote(), and- Strings
# Load `dplyr`
library(dplyr)
# NSE evaluation
select(iris, Sepal.Length, Petal.Length)
# standard evaluation
select_(iris, ~Sepal.Length)
select_(iris, ~Sepal.Length, ~Petal.Length) #works
select_(iris, quote(Sepal.Length), quote(Petal.Length)) # yes!
select_(iris, "Sepal.Length", "Petal.Length", "Species")
Tip: if you want to read more on non-standard evaluation, consider reading the chapter on this topic in Hadley Wickham's Advanced R book.
R Formula Packages
Previously, you have seen that you can create and inspect your formulas using functions such as as.formula, update(), all.vars, ... These were all simple operations and manipulations, but what about advanced manipulations with formulas? Maybe the following packages will be of some interest to you!
Formula Package
Recently, this package was published on CRAN. This package is ideal for those who want to take formulas to the next level. This package extends the base class formula.
More specifically, Formula objects extend the basic formula objects: with this package, you can actually define formulas that accept an additional formula operator | separating multiple parts or that can potentially hold all formula operators (including the pipe character) on the left-hand side to support multiple responses.
Examples of formulas that you will be able to create are:
- Multi-part formulas, such as
y ~ x1 + x2 | u1 + u2 + u3 | v1 + v2 - Multi-response formulas, such as
y1 + y2 ~ x1 + x2 + x3 - Multi-part responses, such as
y1 | y2 + y3 ~ x, and - Combinations of the three above.
# Load package
library(Formula)
# Create formulas
f1 <- y ~ x1 + x2 | z1 + z2 + z3
F1 <- Formula(f1)
# Retrieve the class of `F1`
class(F1)
- 'Formula'
- 'formula'
Note that the functions as.formula() and is.formula() also have been updated in this package: you'll use is.Formula() and as.Formula() instead!
Read more here.
formula.tools
This package was recently released and provides you with "programmatic utilities for manipulating formulas, expressions, calls, assignments and other R Objects". That's a whole lot, but in essence, it all boils down to this: you can use this package to access and modify formula structures as well as to extract and replace names and symbols of those R objects. This package was written by Christopher Brown.
Some things that you might find useful when working with this package are the following:
get.vars(): instead ofall.vars(), this function will extract variable names from various R objects, but all symbols, etc. will be interpolated to names of variables.invert(): you can use this function to invert the operators in an object, such as a formula.is.one.sided(): this function is very handy to determine whether a function is one- or two-sided.
Remember that a formula is one-sided if it looks like this: ~x; It will be two-sided when formulated as x~y.
- ...
There's more to Discover!
Hurray! You have made it through this tutorial on R formulae. If you want to read more about them, definitely check out Hadley Wickham's R for Data Science book, which has a chapter that is totally dedicated to formulas and model families in R.
Check out DataCamp's Getting Started with the Tidyverse: Tutorial.
Can you think of more instances in which you can find formulas or more packages that you can use to manipulate formulas? Feel free to let me know on Twitter: @willems_karlijn.

