NPER() Excel: Understanding Payment Period Calculations

The NPER() function serves as an important financial tool in Excel (and other spreadsheet software) that helps users answer a key question: "How long will it take?" When calculating how many months until a loan is paid off or determining how many years until your retirement savings reach your goal, NPER() delivers the answer.

As part of Excel's financial function family, NPER() is valuable for loan planning, investment analysis, and long-term financial decision-making. In this article, we'll break down how NPER() works, explain its parameters, explore practical examples, and provide helpful tips to help you effectively use this valuable Excel function.

Quick Answer

The NPER() function in Excel calculates the total number of payment periods needed to reach a financial goal. For example, to determine how many monthly payments are needed to pay off a $10,000 loan with $250 monthly payments at 5% annual interest:

=NPER(5%/12, -250, 10000)

The result: approximately 44 months (3.7 years) to pay off the loan completely.

NPER() Excel accountant robot. Image by Dall-E

What Does NPER() Stand For in Excel?

NPER() stands for "Number of Periods" in Excel. True to its name, this function calculates the number of periods required for an investment or loan to reach a target value given a fixed interest rate and consistent payments.

When working with loans, NPER() tells you how many payment periods (months, quarters, years) it will take to fully repay the debt. For investments, it reveals how long it will take to reach your target savings amount with regular contributions.

The function accounts for three main financial components: the regular payment amount, the interest rate per period, and the difference between present and future values. Understanding this relationship is essential because the time component directly impacts the total interest paid on loans or earned on investments.

The general syntax of the NPER() function is:

=NPER(rate, pmt, pv, [fv], [type])

Each parameter plays a specific role:

• rate: The interest rate per period.

• pmt: The payment made each period (must be constant).

• pv: The present value (loan amount or initial investment).

• fv (optional): The desired future value (defaults to 0 if omitted).

• type (optional): Specifies whether payments are due at the end (0) or beginning (1) of each period.

When to Use the NPER() Function

The two main uses of NPER() are to understand loan repayments and investment growth.

Loan repayment calculation

Imagine you want to determine how many months are required to pay off a $25,000 car loan with a $500 monthly payment at an annual interest rate of 4.5%.

The Excel formula would be:

=NPER(4.5%/12, -500, 25000)

When we run this in Excel, we should see the following: 

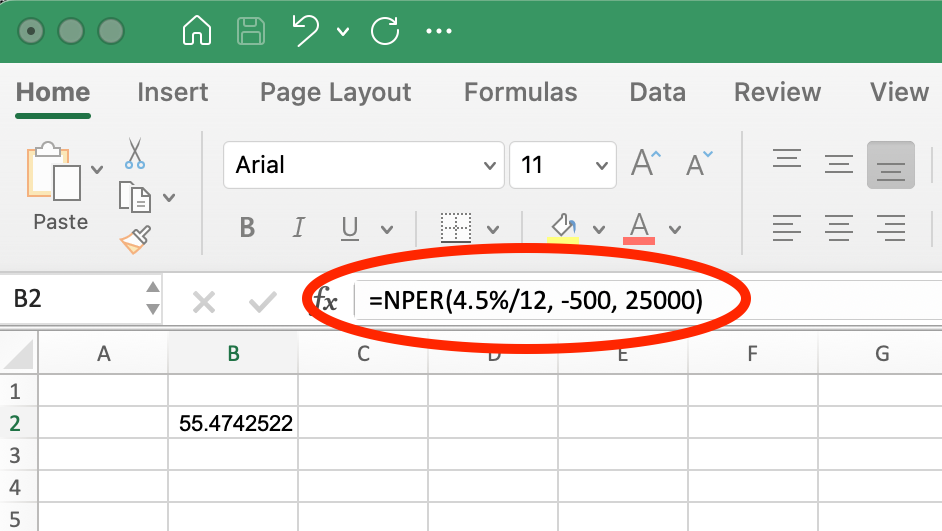
NPER() Function for Car Loan. Image by Author.

This formula returns approximately 55 months. Note that the monthly payment (-500) is entered as a negative value because it represents money flowing out of your pocket. The interest rate is divided by 12 to convert the annual rate to a monthly rate, aligning with the monthly payment schedule.

Investment growth calculation

NPER() is equally valuable for investment planning. Let's say an investor wants to grow $10,000 to $50,000 at an annual interest rate of 5% while contributing $1,000 quarterly.

They would use:

=NPER(5%/4, -1000, 10000, 50000)	

In Excel, we would see: 

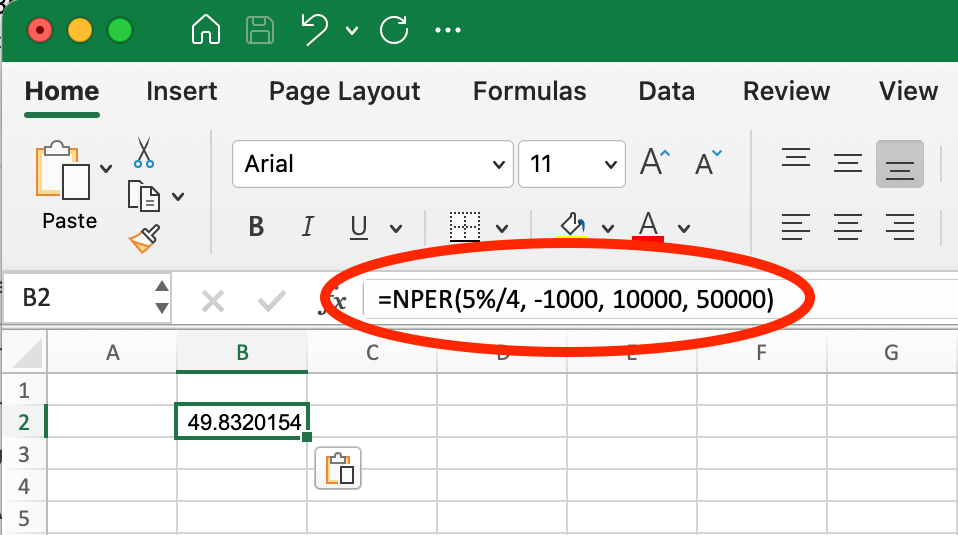
NPER() Function for Investment Growth. Image by Author. 

This formula calculates approximately 50 quarters (12.5 years) to reach the goal. The quarterly payment (-1000) is negative because it's money being invested. The interest rate is divided by 4 to convert from annual to quarterly, matching the quarterly contribution schedule. The future value (50000) is positive because it represents the target amount to be received.

In both examples, NPER() helps answer the "how long" question that's often at the heart of financial planning, making it a useful tool for financial decisions that involve time-based calculations.

Common Errors and Troubleshooting

When working with the NPER() function, you might encounter these common errors:

#NUM! error

This error appears when the given parameters cannot achieve the future value with the specified rate and payment.

Solution: Increase the payment amount or interest rate. For example, if you're trying to pay off a $10,000 loan with $50 monthly payments at 12% annual interest, using =NPER(12%/12, -50, 10000) will return #NUM! because the $50 payment is too small to cover even the monthly interest, making it mathematically impossible to ever pay off the loan.

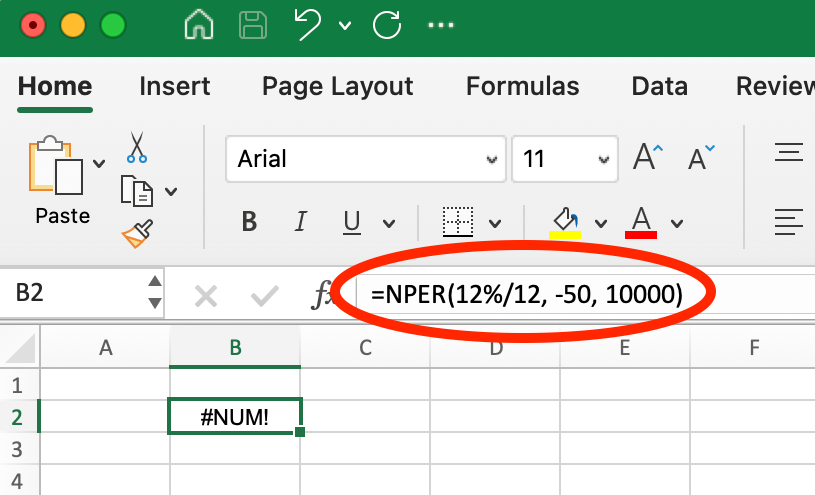
Example of #NUM! Error using NPER(). Image by Author. 

However, if you increase the monthly payment to $200, using =NPER(12%/12, -200, 10000), the function returns approximately 69.7 months (about 5.8 years). 

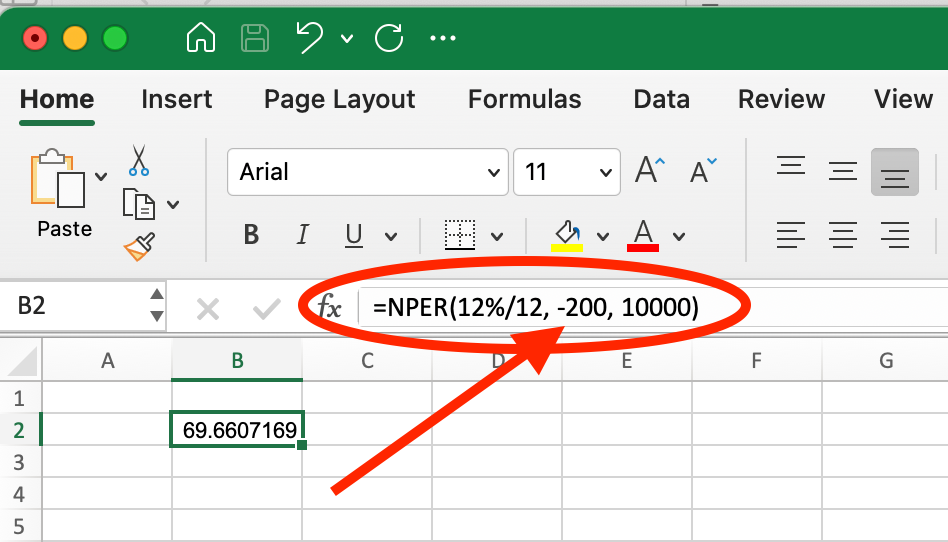
Example of Fixing #NUM! Error by Increasing Payment Amount. Image by Author.

This shows how finding the right payment amount can make the difference between an impossible financial scenario and an achievable goal.

#VALUE! error

This happens when non-numeric values are used in the formula.

Solution: Ensure all inputs are numeric. Check that cells referenced in your formula contain numbers and not text or blank values. If pulling data from other sources, verify the formatting is correct.

Negative NPER() output

A negative result usually indicates incorrect sign conventions in your inputs.

Solution: Adjust pmt and pv values appropriately. Remember the sign convention: positive for incoming values (money you receive) and negative for outgoing values (money you pay out). For loan calculations, the present value (loan amount) should be positive, while the payment should be negative.

Following these sign conventions consistently will help you avoid confusing results and ensure your NPER() calculations provide accurate time estimates for your financial planning.

Advanced Usage of NPER()

Adjusting for different payment intervals

When using the NPER() function with different payment frequencies, you need to properly adjust both the interest rate and payment amount to match the payment interval. Many loan terms are quoted with annual interest rates, but payments often occur more frequently.

Here's how to properly adjust these values:

Monthly payments:

• Interest rate: annual rate/12
• Number of periods: calculated in months

Quarterly payments:

• Interest rate: annual rate/4
• Number of periods: calculated in quarters

Semi-annual payments:

• Interest rate: annual rate/2
• Number of periods: calculated in half-years

Let's look at a $20,000 loan at 6% annual interest with consistent payment amounts across different frequencies:

For monthly payments of $400:

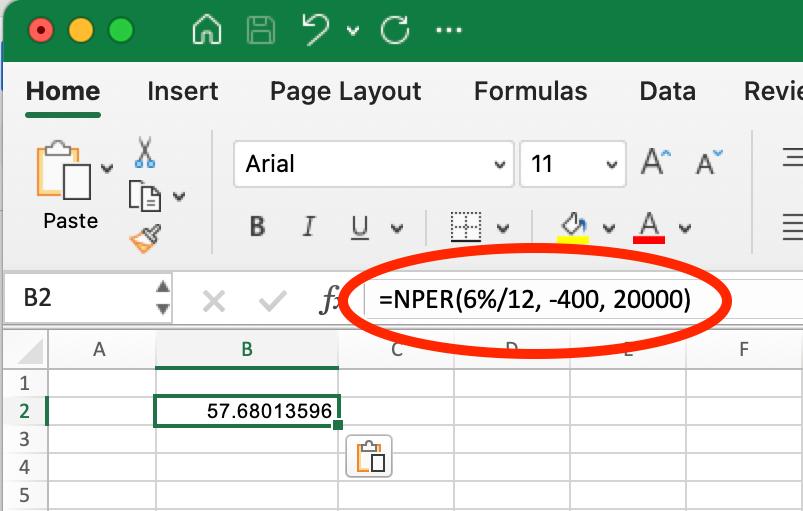
Monthly NPER(). Image by Author. 

​​=NPER(6%/12, -400, 20000)	

This returns approximately 57.7 months (about 4.8 years).

For quarterly payments of $1,200 ($400 × 3 months):

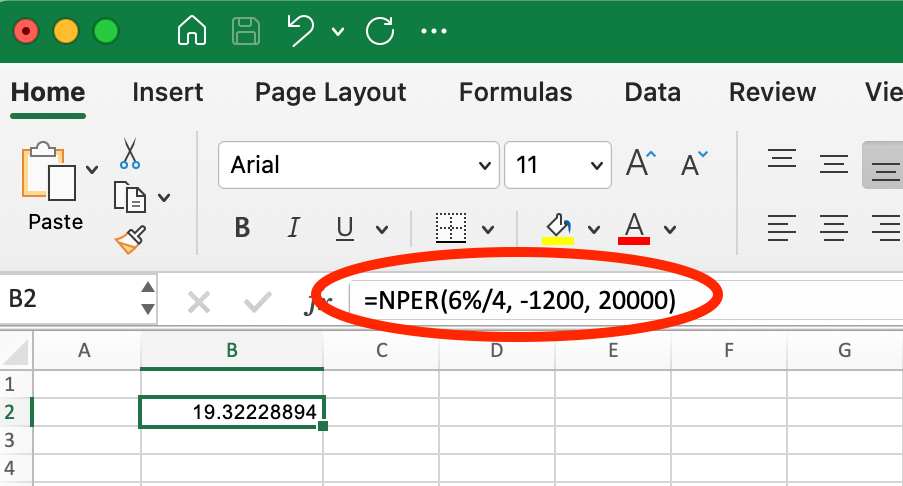
Quarterly NPER(). Image by Author.

=NPER(6%/4, -1200, 20000)	

This returns approximately 19.3 quarters (about 4.8 years).

For semi-annual payments of $2,400 ($400 × 6 months):

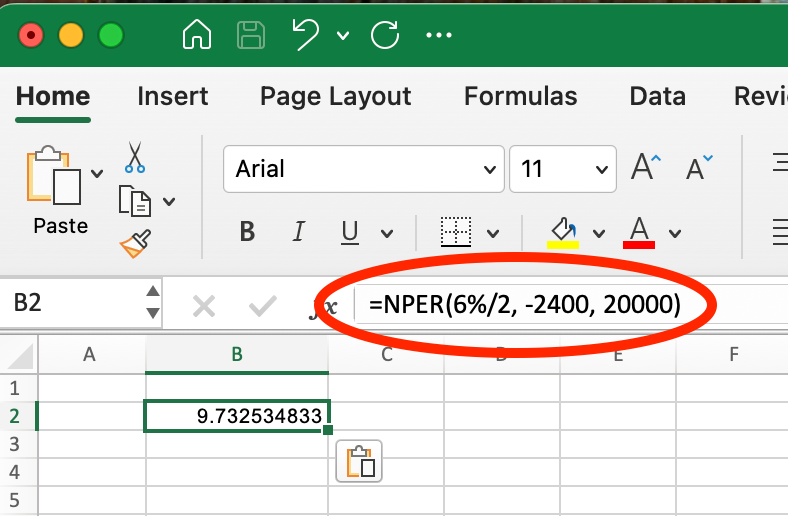
Semi-Annual NPER(). Image by Author.

=NPER(6%/2, -2400, 20000)	

This returns approximately 9.7 periods (about 4.9 years).

Note that the total payoff time is slightly different between payment frequencies due to compounding effects. Less frequent payments generally result in a slightly longer overall repayment period because interest has more time to compound between payments.

When comparing payment scenarios, always ensure you're adjusting both the interest rate and the payment amount proportionally to maintain consistency in your analysis.

Combining with ROUNDUP() to get whole number periods

In practical financial planning, you'll often need to work with whole payment periods since partial payments are typically not an option. The ROUNDUP() function helps convert the decimal output from NPER() into a practical payment schedule.

For example, if we look at the previous scenario where NPER() returns 57.6 monthly payments, by using ROUNDUP() you would get 58:

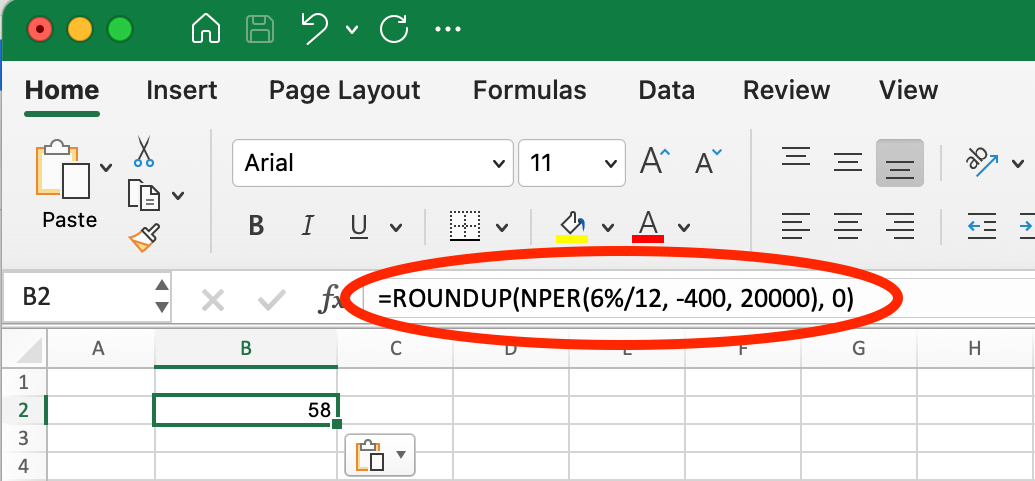
Using ROUNDUP() with NPER(). Image by Author.

=ROUNDUP(NPER(6%/12, -400, 20000), 0)

This formula returns 58, indicating you'll need 58 monthly payments to fully pay off the loan.

Using NPER() with other financial functions

The NPER() function works effectively alongside Excel's other financial functions to create comprehensive financial analyses.

With PV() (present value)

The PV() function calculates the present value (or loan amount) based on payment amount, interest rate, and term. When combined with NPER(), you can explore "what-if" scenarios:

## First, calculate maximum loan amount at 5% with $1,500 monthly payment for 30 years
=PV(5%/12, 30*12, -1500)
## Result: $279,422.43

## Now, see how the original formula confirms the term length
=NPER(5%/12, -1500, 279422.43)
## Result: 360 months (30 years)

## Then, see how increasing payment to $2,000 affects repayment time
=NPER(5%/12, -2000, 279422.43)
## Result: 209.86 months (about 17.5 years)

This analysis shows that by increasing your payment from $1,500 to $2,000 per month on a $279,422.43 loan, you could reduce your repayment period from 30 years to approximately 17.5 years, demonstrating how NPER() can help with financial planning decisions.

With FV() (future value)

Combining NPER() with FV() is particularly useful for retirement and investment planning. This combination helps answer the question: "How long will it take to reach my savings goal?"

For example, if you want to know how many months it would take to save $100,000, starting with nothing, contributing $500 monthly, and earning 7% annual interest:

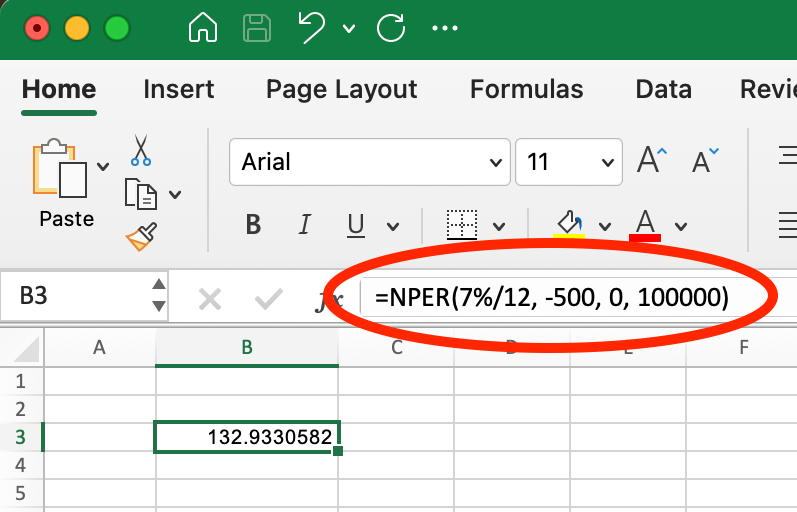
Using NPER() with FV(). Image by Author.

=NPER(7%/12, -500, 0, 100000)

This returns approximately 132.93 months (about 11.1 years), indicating how long you'll need to make those regular contributions to reach your goal.

You can also work backward, first calculating what a particular investment strategy might yield, then determining how adjusting your contributions would affect the timeline:

## First, calculate what 20 years of $500 monthly contributions would grow to at 7%
=FV(7%/12, 20*12, -500, 0)
## Result: $260,463.33

## Then, see how increasing contributions to $750 would change the time needed
=NPER(7%/12, -750, 0, 260463.33)
## Result: 190.36 months (about 15.9 years)

This shows that increasing your monthly contribution from $500 to $750 could help you reach the same $260,463.33 goal in approximately 15.9 years instead of 20 years - a savings of about 4.1 years!

Once you get comfortable, you can combine these two functions into one operation: 

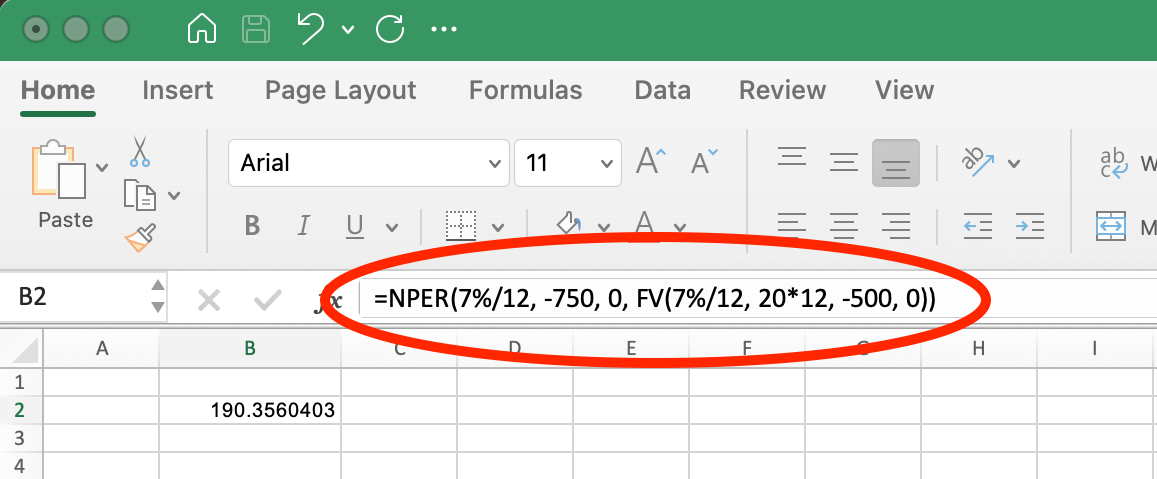
Using NPER() with FV() within One Operation. Image by Author.

Using NPER() with FV() this way allows you to experiment with different savings rates and timeframes to find the approach that best matches your financial goals and constraints.

With RATE()

The RATE() function helps you determine the interest rate for a loan or investment with known parameters. When used with NPER(), you can analyze how different interest rates affect repayment periods.

For example, suppose you have a $300,000 mortgage with a $1,500 monthly payment. You can first calculate what interest rate this corresponds to over a 30-year (360-month) term:

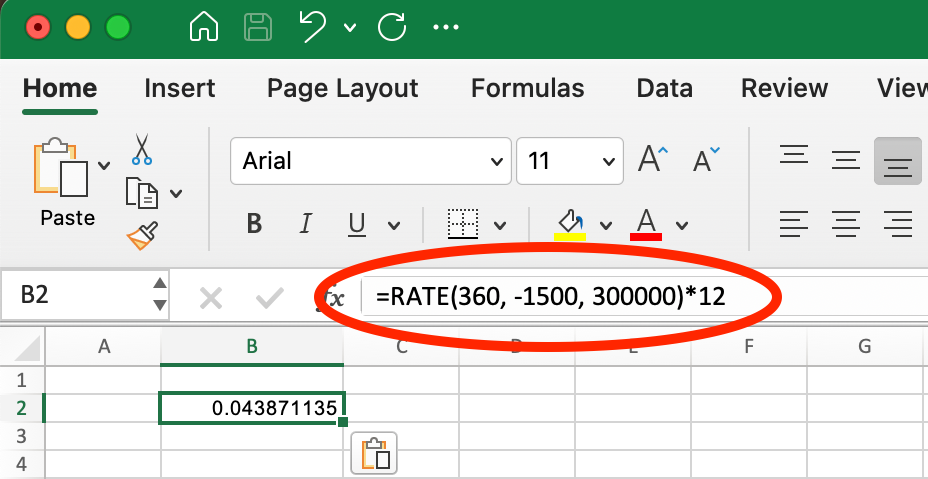
Example of RATEI() for Mortage Loan. Image by Author.

=RATE(360, -1500, 300000)*12

This returns approximately 4.39% annual interest. Now you can analyze how changing market conditions or refinancing at different rates would affect your payoff timeline:

## Original scenario: mortgage at 4.39%
=NPER(4.39%/12, -1500, 300000)
## Result: 360 months (30 years)

## If interest rates drop to 4%
=NPER(4%/12, -1500, 300000)
## Result: 330.13 months (about 27.5 years)

## If interest rates rise to 5%
=NPER(5%/12, -1500, 300000)
## Result: 430.92 months (about 35.9 years)

This analysis shows how even a seemingly small change in interest rate can dramatically impact your loan term. A 0.39% decrease in interest rate (from 4.39% to 4%) would shorten your repayment period by approximately 2.5 years, while a 0.61% increase (from 4.39% to 5%) would extend it by nearly 6 years—all without changing your monthly payment amount.

This approach helps evaluate refinancing opportunities or understand the impact of variable-rate loans when interest rates fluctuate.

Key Takeaways

The NPER() function calculates the number of periods required to pay off a loan or reach an investment goal. Here are the essential points to remember:

• NPER() requires inputs like interest rate, payment amount, and present value, with optional future value and payment type parameters.

• Always match your rate period with your payment frequency. For monthly payments with an annual interest rate, divide the rate by 12 and express your result in months.

• Sign conventions matter: for loan calculations, the present value (loan amount) should be positive, while the payment should be negative.

• When NPER() returns a #NUM! error, it typically means your payment amount is too small relative to the interest rate—the loan would never be paid off.

• For practical planning, use ROUNDUP() with NPER() to get whole number periods since partial payments are usually not an option in real-world scenarios.

• NPER() works effectively with other financial functions like PV(), FV() and RATE() to create comprehensive financial analyses and "what-if" scenarios.

Understanding and correctly applying the NPER() function will help you make more informed financial decisions about loans, investments, and savings plans.

Conclusion

The NPER() function is a valuable tool in Excel's financial function library that answers one of the most common questions in personal and business finance: "How long will it take?" Whether you're calculating loan repayment timelines, planning for retirement savings, or evaluating investment opportunities, NPER() provides clear insights into the time dimension of your financial decisions.

By using the NPER() function effectively, you gain the ability to:

• Determine precise loan payoff timelines
• Plan more effectively for savings goals
• Understand how adjusting payment amounts impacts your financial timeline
• See how interest rate changes affect the length of financial commitments

Remember that NPER() works best when used alongside Excel's other financial functions. Combining it with PMT(), RATE(), PV(), and FV() allows you to build comprehensive financial models that can guide important decisions about borrowing, saving, and investing. For a comprehensive guide on the PMT() function, we recommend visiting our dedicated tutorial on this topic. 

For those looking to expand their Excel financial analysis skills, consider exploring DataCamp's Financial Modeling in Excel course, which covers cash flows, scenario analysis, time value of money calculations, and other essential financial concepts that build upon the foundations you've learned here.