ANOVA

Si has estado analizando diseños ANOVA en paquetes estadísticos tradicionales, es probable que encuentres el enfoque de R menos coherente y fácil de usar. Puedes encontrar una buena presentación en línea sobre ANOVA en R en la sección ANOVA</a > del Proyecto Personalidad. (Nota: He comprobado que estas páginas se visualizan bien en los navegadores Chrome y Safari, pero pueden aparecer distorsionadas en iExplorer).

1. Ajustar un modelo

En los siguientes ejemplos, las letras minúsculas son variables numéricas y las mayúsculas son factores.

# One Way Anova (Completely Randomized Design)
fit <- aov(y ~ A, data=mydataframe)

# Randomized Block Design (B is the blocking factor)
fit <- aov(y ~ A + B, data=mydataframe)

# Two Way Factorial Design
fit <- aov(y ~ A + B + A:B, data=mydataframe)
fit <- aov(y ~ A*B, data=mydataframe)
# same thing

# Analysis of Covariance
fit <- aov(y ~ A + x, data=mydataframe)

Para los diseños intra-sujetos, hay que reorganizar el marco de datos de modo que cada medición en un sujeto sea una observación independiente. Ver R y Análisis de Varianza.

# One Within Factor
fit <- aov(y~A+Error(Subject/A),data=mydataframe)

# Two Within Factors W1 W2, Two Between Factors B1 B2
fit <- aov(y~(W1*W2*B1*B2)+Error(Subject/(W1*W2))+(B1*B2),
   data=mydataframe)

2. Mira las parcelas de diagnóstico

Los gráficos de diagnóstico permiten comprobar la heteroscedasticidad, la normalidad y las observaciones influyentes.```R layout(matrix(c(1,2,3,4),2,2)) # Disposición opcional

plot(fit) # gráficos de diagnóstico

Para más detalles sobre la evaluación de los requisitos de las pruebas, consulta [(M)ANOVA Supuestos](/stats/anovaAssumptions.html). ### 3. Evaluar los efectos del modelo **ADVERTENCIA** : R proporciona [SS secuencial de tipo I](http://afni.nimh.nih.gov/sscc/gangc/SS.html), no el [SS marginal de tipo III](http://afni.nimh.nih.gov/sscc/gangc/SS.html) por defecto que informan SAS y SPSS. En un diseño no ortogonal con más de un término en el lado derecho de la ecuación, ¡el **orden importará** (es decir, A+B y B+A producirán resultados _diferentes_)! Necesitaremos utilizar la función **gota1( )** para obtener los resultados familiares de Tipo III. Comparará cada término con el modelo completo. Como alternativa, podemos utilizar anova(fit.modelo1, fit.modelo2) para comparar modelos anidados directamente. ```R summary(fit) # mostrar tabla ANOVA tipo I drop1(fit,~.,test="F") # pruebas SS y F tipo III

Existen alternativas no paramétricas y de remuestreo.

Comparaciones múltiples

Puedes obtener las pruebas HSD de Tukey utilizando la función que aparece a continuación. Por defecto, calcula comparaciones post hoc en cada factor del modelo. Puedes especificar factores concretos como opción. De nuevo, ¡recuerda que los resultados se basan en el Tipo I SS!

# Tukey Honestly Significant Differences
TukeyHSD(fit) # where fit comes from aov()

Visualizar los resultados

Utiliza diagramas de caja y diagramas de líneas para visualizar las diferencias entre grupos. También hay dos funciones diseñadas específicamente para visualizar las diferencias de medias en los trazados de ANOVA. interaction.plot( ) del paquete base stats produce trazados para interacciones bidireccionales. plotmeans( ) del paquete gplots</a >produce trazados de medias para factores únicos, e incluye intervalos de confianza.

# Two-way Interaction Plot
attach(mtcars)
gears <- factor(gears)
cyl <- factor(cyl)
interaction.plot(cyl, gear, mpg, type="b", col=c(1:3),
   leg.bty="o", leg.bg="beige", lwd=2, pch=c(18,24,22),
   xlab="Number of Cylinders",
   ylab="Mean Miles Per Gallon",
   main="Interaction Plot")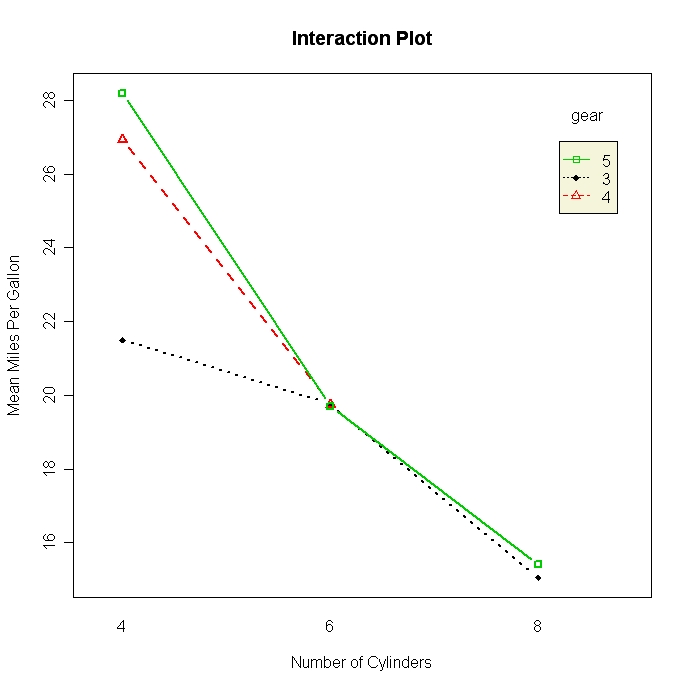

# Plot Means with Error Bars
library(gplots)
attach(mtcars)
cyl <- factor(cyl)
plotmeans(mpg~cyl,xlab="Number of Cylinders",
  ylab="Miles Per Gallon", main="Mean Plot\nwith 95% CI")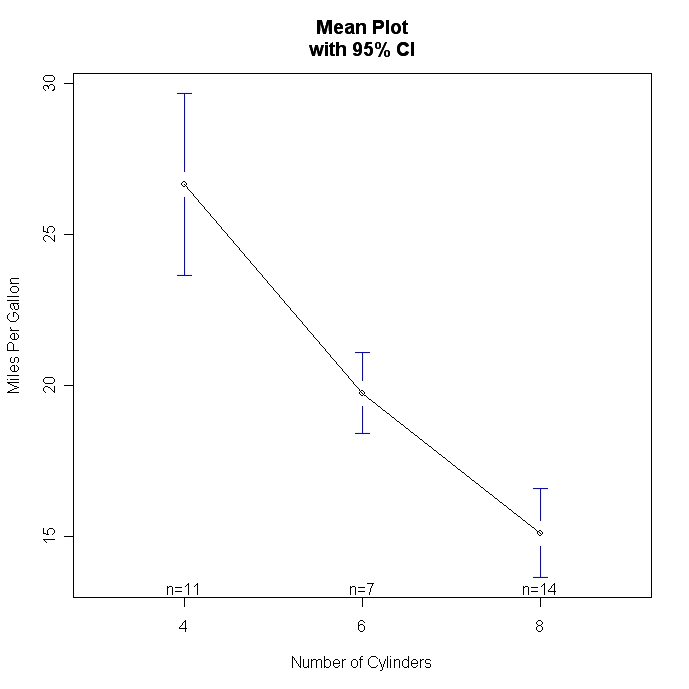

MANOVA

Si hay más de una variable dependiente (de resultado), puedes probarlas simultáneamente mediante un análisis multivariante de la varianza (MANOVA). En el ejemplo siguiente, sea Y una matriz cuyas columnas son las variables dependientes.

# 2x2 Factorial MANOVA with 3 Dependent Variables.
Y <- cbind(y1,y2,y3)
fit <- manova(Y ~ A*B)
summary(fit, test="Pillai")

Otras opciones de prueba son "Wilks", "Hotelling-Lawley" y "Roy". Utiliza summary.aov( ) para obtener estadísticas univariantes. TukeyHSD( ) y plot( ) no funcionarán con un ajuste MANOVA. Ejecuta cada variable dependiente por separado para obtenerlas. Al igual que el ANOVA, los resultados del MANOVA en R se basan en el Tipo I SS. Para obtener SS de tipo III, varía el orden de las variables en el modelo y vuelve a ejecutar los análisis. Por ejemplo, ajusta y~A*B para el efecto Tipo III B e y~B*A para el efecto Tipo III A.</span >

Ir más lejos

R dispone de excelentes funciones para ajustar modelos lineales y lineales generalizados de efectos mixtos. La última implementación está en el paquete lme4. Consulta el artículo de R News sobre Ajuste de modelos lineales mixtos en R</a > para obtener más detalles .