ANOVA

Wenn du ANOVA-Designs in herkömmlichen Statistikpaketen analysiert hast, wirst du den Ansatz von R wahrscheinlich weniger kohärent und benutzerfreundlich finden. Eine gute Online-Präsentation zur ANOVA in R findest du im Abschnitt ANOVA</a > des Personality Project. (Hinweis: Ich habe festgestellt, dass diese Seiten in den Browsern Chrome und Safari gut dargestellt werden, aber im iExplorer verzerrt erscheinen können).

1. Ein Modell anpassen

In den folgenden Beispielen stehen Kleinbuchstaben für numerische Variablen und Großbuchstaben für Faktoren.

# One Way Anova (Completely Randomized Design)
fit <- aov(y ~ A, data=mydataframe)

# Randomized Block Design (B is the blocking factor)
fit <- aov(y ~ A + B, data=mydataframe)

# Two Way Factorial Design
fit <- aov(y ~ A + B + A:B, data=mydataframe)
fit <- aov(y ~ A*B, data=mydataframe)
# same thing

# Analysis of Covariance
fit <- aov(y ~ A + x, data=mydataframe)

Bei einem Within-Subject-Design muss der Datenrahmen so angeordnet werden, dass jede Messung an einem Probanden eine separate Beobachtung ist. Siehe R und Varianzanalyse.

# One Within Factor
fit <- aov(y~A+Error(Subject/A),data=mydataframe)

# Two Within Factors W1 W2, Two Between Factors B1 B2
fit <- aov(y~(W1*W2*B1*B2)+Error(Subject/(W1*W2))+(B1*B2),
   data=mydataframe)

2. Diagnostische Diagramme ansehen

Diagnostische Plots bieten Prüfungen auf Heteroskedastizität, Normalität und einflussreiche Beobachtungen.```R layout(matrix(c(1,2,3,4),2,2)) # optionales Layout

plot(fit) # Diagnoseplots

Einzelheiten zur Bewertung der Testanforderungen findest du unter [(M)ANOVA-Annahmen](/stats/anovaAssumptions.html). ### 3. Auswertung der Modelleffekte **WARNUNG** : R bietet [Typ I sequentielle SS](http://afni.nimh.nih.gov/sscc/gangc/SS.html) und nicht den Standard [Typ III marginale SS](http://afni.nimh.nih.gov/sscc/gangc/SS.html), der von SAS und SPSS gemeldet wird. Bei einem nicht-orthogonalen Design mit mehr als einem Term auf der rechten Seite der Gleichung spielt die **Reihenfolge eine Rolle** (d.h. A+B und B+A ergeben _unterschiedliche_ Ergebnisse)! Wir müssen die Funktion **drop1( )** verwenden, um die bekannten Ergebnisse vom Typ III zu erhalten. Er vergleicht jeden Begriff mit dem vollständigen Modell. Alternativ können wir auch anova(fit.model1, fit.model2) verwenden, um verschachtelte Modelle direkt zu vergleichen. ```R summary(fit) # Typ I ANOVA Tabelle anzeigen drop1(fit,~.,test="F") # Typ III SS und F Tests

Es gibt nichtparametrische und Resampling-Alternativen.

Mehrere Vergleiche

Du kannst Tukey HSD-Tests mit der unten stehenden Funktion durchführen. Standardmäßig werden Post-Hoc-Vergleiche für jeden Faktor des Modells berechnet. Du kannst bestimmte Faktoren als Option angeben. Auch hier gilt: Die Ergebnisse basieren auf Typ I SS!

# Tukey Honestly Significant Differences
TukeyHSD(fit) # where fit comes from aov()

Ergebnisse visualisieren

Verwende Boxplots und Liniendiagramme, um Gruppenunterschiede zu visualisieren. Es gibt auch zwei Funktionen, die speziell für die Visualisierung von Mittelwertunterschieden in ANOVA-Layouts entwickelt wurden. interaction.plot( ) im Basispaket stats erzeugt Plots für Zwei-Wege-Interaktionen. plotmeans( ) im gplots</a >Paket erzeugt Mittelwertplots für einzelne Faktoren und enthält Konfidenzintervalle.

# Two-way Interaction Plot
attach(mtcars)
gears <- factor(gears)
cyl <- factor(cyl)
interaction.plot(cyl, gear, mpg, type="b", col=c(1:3),
   leg.bty="o", leg.bg="beige", lwd=2, pch=c(18,24,22),
   xlab="Number of Cylinders",
   ylab="Mean Miles Per Gallon",
   main="Interaction Plot")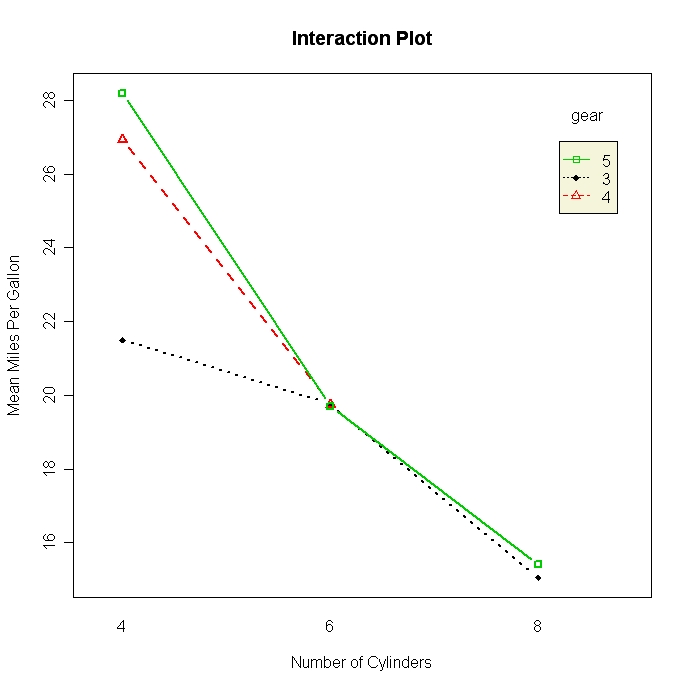

# Plot Means with Error Bars
library(gplots)
attach(mtcars)
cyl <- factor(cyl)
plotmeans(mpg~cyl,xlab="Number of Cylinders",
  ylab="Miles Per Gallon", main="Mean Plot\nwith 95% CI")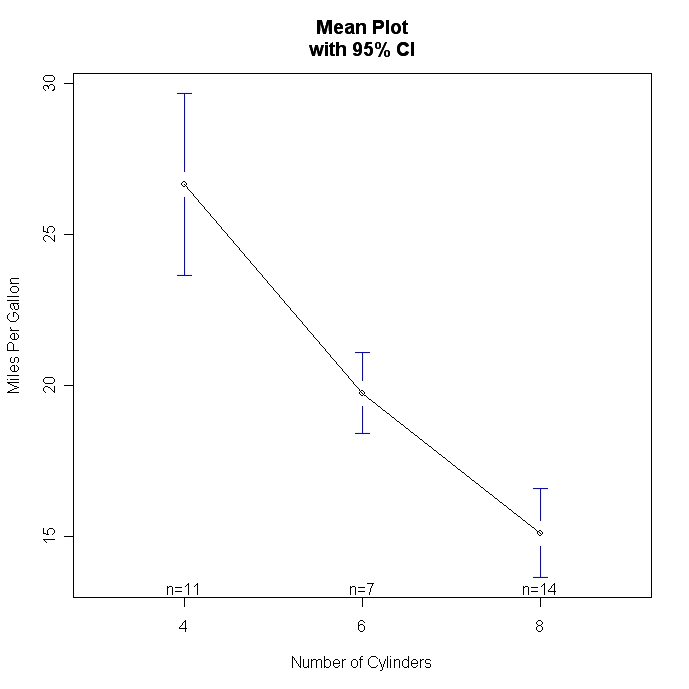

MANOVA

Wenn es mehr als eine abhängige (Ergebnis-)Variable gibt, kannst du sie mit einer multivariaten Varianzanalyse (MANOVA) gleichzeitig testen. Im folgenden Beispiel soll Y eine Matrix sein, deren Spalten die abhängigen Variablen sind.

# 2x2 Factorial MANOVA with 3 Dependent Variables.
Y <- cbind(y1,y2,y3)
fit <- manova(Y ~ A*B)
summary(fit, test="Pillai")

Andere Testoptionen sind "Wilks", "Hotelling-Lawley" und "Roy". Verwende summary.aov( ), um univariate Statistiken zu erhalten. TukeyHSD( ) und plot( ) funktionieren nicht mit einer MANOVA-Anpassung. Führe jede abhängige Variable separat aus, um sie zu erhalten. Wie bei der ANOVA basieren auch die MANOVA-Ergebnisse in R auf dem Typ I SS. Um Typ III SS zu erhalten, ändere die Reihenfolge der Variablen im Modell und führe die Analysen erneut durch. Füge zum Beispiel y~A*B für den Typ III B-Effekt und y~B*A für den Typ III A-Effekt ein.</span >

Weiter gehen

R verfügt über hervorragende Möglichkeiten zur Anpassung linearer und verallgemeinerter linearer Modelle mit gemischten Effekten. Die letzte Implementierung ist im Paket lme4. Weitere Informationen findest du im R News Artikel über die Anpassung von gemischten linearen Modellen in R</a > .