Gráficos de probabilidad en R
Esta sección describe la creación de gráficos de probabilidad en R, tanto con fines didácticos como para el análisis de datos.
Gráficos de probabilidad para la enseñanza y la demostración
Cuando era profesor universitario y enseñaba estadística, tenía que dibujar distribuciones normales a mano. Siempre salían con aspecto de conejitos. ¿Qué puedo decir?
Con R es fácil dibujar distribuciones de probabilidad y demostrar conceptos estadísticos. A continuación se indican algunas de las distribuciones de probabilidad más comunes disponibles en R.
| distribución | Nombre | distribución | Nombre |
| Beta | beta | Lognormal | lnorm |
| Binomial | binom | Binomio negativo | nbinom |
| Cauchy | cauchy | Normal | norma |
| Chisquare | chisq | Poisson | pois |
| Exponencial | exp | Alumno t | t |
| F | f | Uniforme | unif |
| Gamma | gamma | Tukey | tukey |
| Geométrico | geom | Weibull | weib |
| Hipergeométrico | hiper | Wilcoxon | wilcox |
| Logística | logis |
Para obtener una lista completa, consulta Distribuciones estadísticas en la wiki de R. Las funciones disponibles para cada distribución siguen este formato:
| nombre | description |
| d nombre( ) | densidad o función de probabilidad |
| p nombre( ) | función de densidad acumulativa |
| q nombre( ) | función cuantil |
| R_name_( ) | desviaciones aleatorias |
Por ejemplo, pnorm(0) =0,5 (el área bajo la curva normal estándar a la izquierda de cero). qnorm(0,9) = 1,28 (1,28 es el percentil 90 de la distribución normal estándar). rnorm(100) genera 100 desviaciones aleatorias de una distribución normal estándar.
Cada función tiene parámetros específicos de esa distribución. Por ejemplo, rnorm(100, m=50, sd=10) genera 100 desviaciones aleatorias de una distribución normal con media 50 y desviación típica 10.
Puedes utilizar estas funciones para demostrar diversos aspectos de las distribuciones de probabilidad. A continuación se dan dos ejemplos comunes.
# Display the Student's t distributions with various
# degrees of freedom and compare to the normal distribution
x <- seq(-4, 4, length=100)
hx <- dnorm(x)
degf <- c(1, 3, 8, 30)
colors <- c("red", "blue", "darkgreen", "gold", "black")
labels <- c("df=1", "df=3", "df=8", "df=30", "normal")
plot(x, hx, type="l", lty=2, xlab="x value",
ylab="Density", main="Comparison of t Distributions")
for (i in 1:4){
lines(x, dt(x,degf[i]), lwd=2, col=colors[i])
}
legend("topright", inset=.05, title="Distributions",
labels, lwd=2, lty=c(1, 1, 1, 1, 2), col=colors)# Children's IQ scores are normally distributed with a
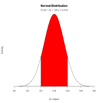
# mean of 100 and a standard deviation of 15. What
# proportion of children are expected to have an IQ between
# 80 and 120?
mean=100; sd=15
lb=80; ub=120
x <- seq(-4,4,length=100)*sd + mean
hx <- dnorm(x,mean,sd)
plot(x, hx, type="n", xlab="IQ Values", ylab="",
main="Normal Distribution", axes=FALSE)
i <- x >= lb & x <= ub
lines(x, hx)
polygon(c(lb,x[i],ub), c(0,hx[i],0), col="red")
area <- pnorm(ub, mean, sd) - pnorm(lb, mean, sd)
result <- paste("P(",lb,"< IQ <",ub,") =",
signif(area, digits=3))
mtext(result,3)
axis(1, at=seq(40, 160, 20), pos=0)Para una visión completa del trazado de probabilidades en R, consulta Distribuciones de probabilidad, de Vincent Zonekynd.
Ajuste de distribuciones
Existen varios métodos para ajustar distribuciones en R. Aquí tienes algunas opciones.
Puedes utilizar la función qqnorm( ) para crear un gráfico Cuantil-Cuantil que evalúe el ajuste de los datos de la muestra a la distribución normal. De forma más general, la función qqplot( ) crea un gráfico Cuantil-Cuantil para cualquier distribución teórica.
# Q-Q plots
par(mfrow=c(1,2))
# create sample data
x <- rt(100, df=3)
# normal fit
qqnorm(x);
qqline(x)
# t(3Df) fit
qqplot(rt(1000,df=3), x, main="t(3) Q-Q Plot",
ylab="Sample Quantiles")
abline(0,1)La función fitdistr( ) del paquete MASS proporciona el ajuste de máxima verosimilitud de las distribuciones univariantes. El formato es fitdistr(x, funcióndensidad) donde x son los datos de la muestra y funcióndensidad es una de las siguientes: "beta", "cauchy", "chi-cuadrado", "exponencial", "f", "gamma", "geométrica", "log-normal"lognormal", "logística", "binomial negativa", "normal", "Poisson", "t" o "weibull".
# Estimate parameters assuming log-Normal distribution
# create some sample data
x <- rlnorm(100)
# estimate paramters
library(MASS)
fitdistr(x, "lognormal")Por último, R dispone de una amplia gama de pruebas de bondad de ajuste para evaluar si es razonable suponer que una muestra aleatoria procede de una distribución teórica especificada. Entre ellas se incluyen chi-cuadrado, Kolmogorov-Smirnov y Anderson-Darling.
Para más detalles sobre el ajuste de distribuciones, consulta Ajuste de distribuciones con R, de Vito Ricci.
Practicar
Prueba este curso interactivo sobre análisis exploratorio de datos.