Regresión múltiple (lineal) en R

R ofrece un amplio soporte para la regresión lineal múltiple. Los temas que figuran a continuación se ofrecen en orden de complejidad creciente.

Ajuste del modelo

# Multiple Linear Regression Example

fit <- lm(y ~ x1 + x2 + x3, data=mydata)
summary(fit) # show results

# Other useful functions
coefficients(fit) # model coefficients
confint(fit, level=0.95) # CIs for model parameters

fitted(fit) # predicted values
residuals(fit) # residuals
anova(fit) # anova table
vcov(fit) # covariance matrix for model parameters
influence(fit) # regression diagnostics

Parcelas de diagnóstico

Los gráficos de diagnóstico permiten comprobar la heteroscedasticidad, la normalidad y las observaciones influyentes.

# diagnostic plots
layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page
plot(fit)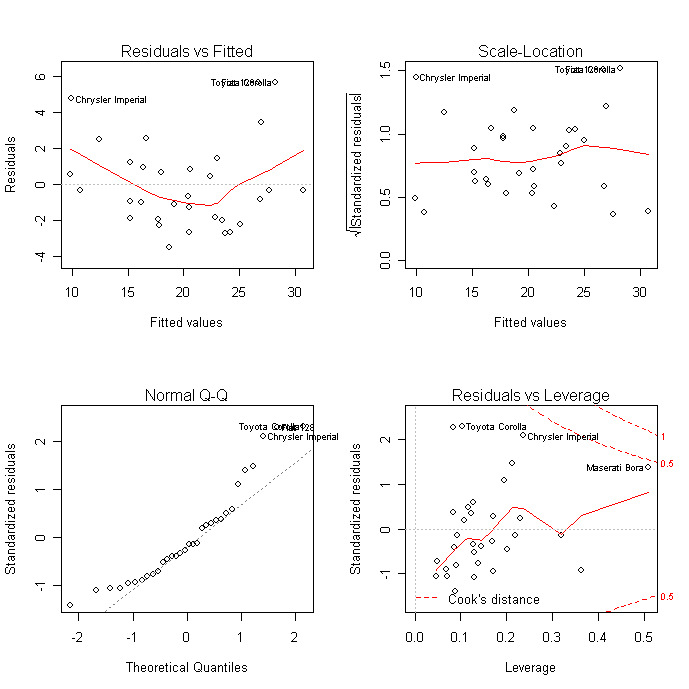

Para una evaluación más exhaustiva del ajuste del modelo, consulta los diagnósticos de regresión o los ejercicios de este curso interactivo</a > sobre Aprendizaje Supervisado en R: Regresión.

Comparación de modelos

Puedes comparar modelos anidados con la función anova( ). El código siguiente proporciona una prueba simultánea de que x3 y x4 se suman a la predicción lineal por encima de x1 y x2.

# compare models
fit1 <- lm(y ~ x1 + x2 + x3 + x4, data=mydata)
fit2 <- lm(y ~ x1 + x2)
anova(fit1, fit2)

Validación cruzada

Puedes hacer una validación cruzada K-Fold</a >utilizando la función cv.lm( ) del paquete DAAG.

# K-fold cross-validation
library(DAAG)
cv.lm(df=mydata, fit, m=3) # 3 fold cross-validation

Suma el MSE de cada pliegue, divídelo por el número de observaciones y saca la raíz cuadrada para obtener el error estándar de estimación validado cruzadamente.

Puedes evaluar la contracción de R2 mediante la validación cruzada K-fold. Utiliza la función crossval() del paquete paquete bootstrap</a ></strong >, haz lo siguiente:

# Assessing R2 shrinkage using 10-Fold Cross-Validation

fit <- lm(y~x1+x2+x3,data=mydata)

library(bootstrap)
# define functions
theta.fit <- function(x,y){lsfit(x,y)}
theta.predict <- function(fit,x){cbind(1,x)%*%fit$coef}

# matrix of predictors
X
<- as.matrix(mydata[c("x1","x2","x3")])
# vector of predicted values
y <- as.matrix(mydata[c("y")])

results <- crossval(X,y,theta.fit,theta.predict,ngroup=10)
cor(y, fit$fitted.values)**2 # raw R2
cor(y,results$cv.fit)**2 # cross-validated R2

Selección de variables

La selección de un subconjunto de variables predictoras a partir de un conjunto mayor (por ejemplo, la selección por pasos) es un tema controvertido. Puedes realizar la selección por pasos (hacia delante, hacia atrás, ambos) utilizando la función stepAIC( ) del paquete MASS. stepAIC( ) realiza la selección por pasos del modelo mediante el AIC exacto.

# Stepwise Regression
library(MASS)
fit <- lm(y~x1+x2+x3,data=mydata)
step <- stepAIC(fit, direction="both")
step$anova # display results

También puedes realizar una regresión de todos los subconjuntos utilizando la función leaps( ) del paquete leaps. En el código siguiente nbest indica el número de subconjuntos de cada tamaño que hay que informar. Aquí se informará de los diez mejores modelos para cada tamaño de subconjunto (1 predictor, 2 predictores, etc.).

# All Subsets Regression
library(leaps)
attach(mydata)
leaps<-regsubsets(y~x1+x2+x3+x4,data=mydata,nbest=10)
# view results
summary(leaps)
# plot a table of models showing variables in each model.
#
models are ordered by the selection statistic.
plot(leaps,scale="r2")
# plot statistic by subset size
library(car)
subsets(leaps, statistic="rsq")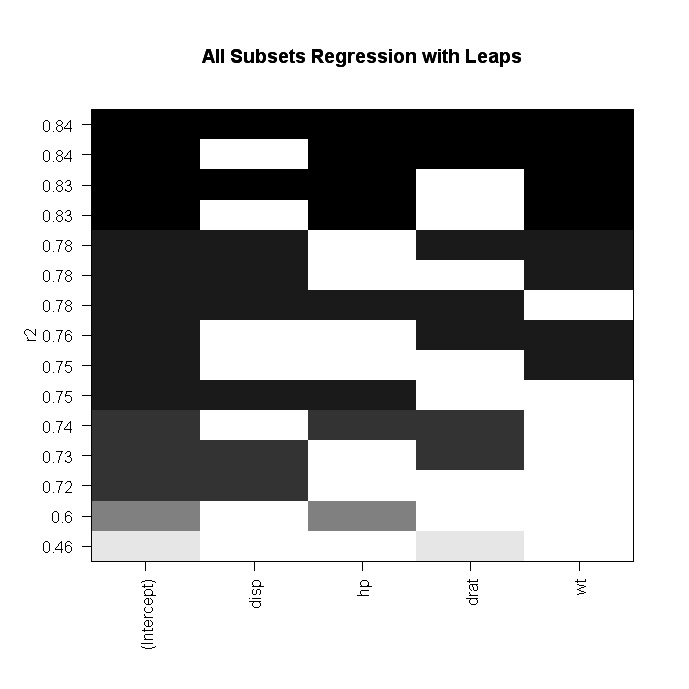

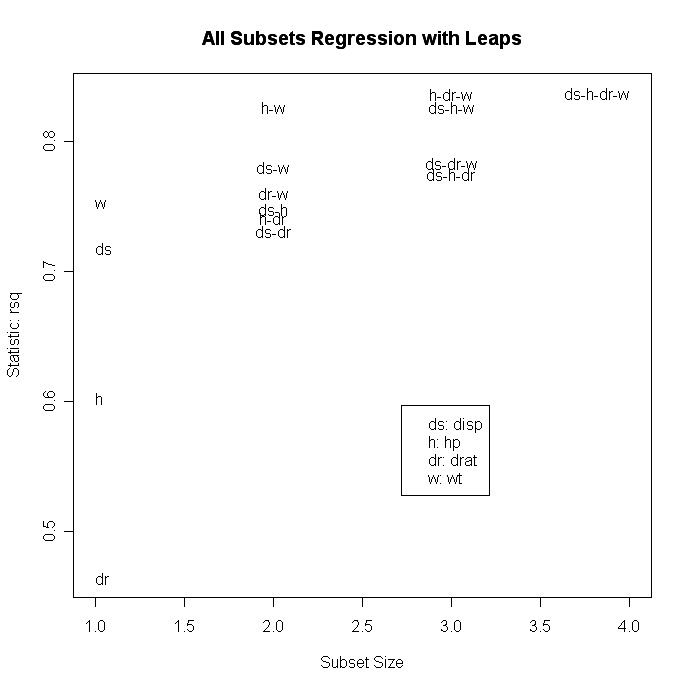
Otras opciones de plot( ) son bic, Cp y adjr2. Otras opciones para trazar consubconjunto( ) son bic, cp, adjr2 y rss.

Importancia relativa

El paquete relaimpo</a > proporciona medidas de importancia relativa para cada uno de los predictores del modelo. Consulta help(calc.relimp) para obtener más detalles sobre las cuatro medidas de importancia relativa proporcionadas.

# Calculate Relative Importance for Each Predictor
library(relaimpo)
calc.relimp(fit,type=c("lmg","last","first","pratt"),
   rela=TRUE)

# Bootstrap Measures of Relative Importance (1000 samples)
boot <- boot.relimp(fit, b = 1000, type = c("lmg",
  "last", "first", "pratt"), rank = TRUE,
  diff = TRUE, rela = TRUE)
booteval.relimp(boot) # print result
plot(booteval.relimp(boot,sort=TRUE)) # plot result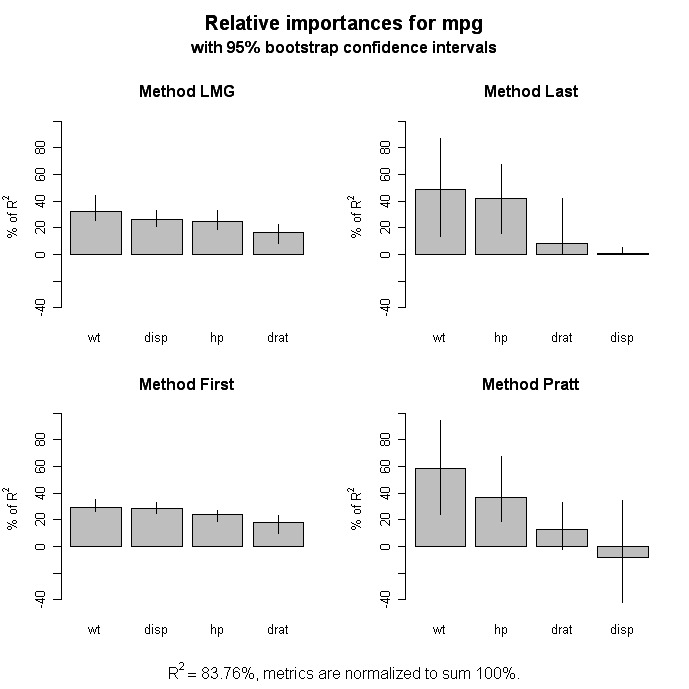

Mejoras gráficas

El paquete Auto ofrece una amplia variedad de gráficos para la regresión, incluidos gráficos de variables añadidas y gráficos de diagnóstico y de dispersión mejorados.

Ir más lejos

Regresión no lineal

El paquete nls proporciona funciones para la regresión no lineal. Consulta Regresión no lineal y mínimos cuadrados no lineales</a > de John Fox para obtener una visión general. Huet y colegas, Herramientas estadísticas para la regresión no lineal: A Practical Guide with S-PLUS and R Examples</a > es un valioso libro de consulta.

Regresión robusta

Hay muchas funciones en R para ayudar con la regresión robusta. Por ejemplo, puedes realizar una regresión robusta con la función rlm( ) del paquete MASS. John Fox (¿quién si no?) Regresión robusta</a > proporciona una buena visión general de partida. El sitio web de Computación Estadística de la UCLA tiene Ejemplos de regresión robusta</a > .

El paquete robusto proporciona una completa biblioteca de métodos robustos, incluida la regresión. El paquete robustbase</a > también proporciona estadísticas robustas básicas, incluidos métodos de selección de modelos. Y David Olive ha proporcionado una detallada reseña en línea de Applied Robust Statistics</a > con ejemplos de código R .

Practicar

Este curso de aprendizaje automático en R</a > incluye ejercicios de regresión múltiple y validación cruzada .