Evaluar los supuestos de las pruebas clásicas en R

En los procedimientos paramétricos clásicos solemos suponer normalidad y varianza constante para el término de error del modelo. Aquí se discuten métodos para explorar estos supuestos en un marco ANOVA/ANCOVA/MANOVA. Los diagnósticos de regresión se tratan en la regresión lineal múltiple.

Valores atípicos

Dado que los valores atípicos pueden afectar gravemente a la normalidad y a la homogeneidad de la varianza, primero se describen los métodos para detectar las observaciones atípicas.

La función aq.plot() del paquete mvoutlier</a > te permite identificar valores atípicos multivariantes trazando las distancias de Mahalanobis robustas ordenadas al cuadrado de las observaciones frente a la función de distribución empírica del _MD2i. La entrada consiste en una matriz o marco de datos. La función produce 4 gráficos y devuelve un vector booleano que identifica los valores atípicos.

# Detect Outliers in the MTCARS Data
library(mvoutlier)
outliers <-
aq.plot(mtcars[c("mpg","disp","hp","drat","wt","qsec")])
outliers # show list of outliers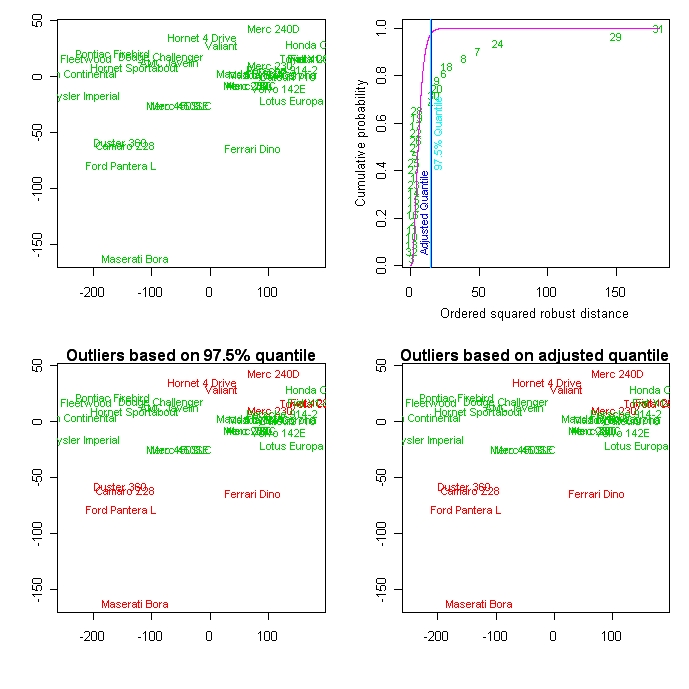

Normalidad univariante

Puedes evaluar la normalidad de una variable mediante un gráfico Q-Q.

# Q-Q Plot for variable MPG
attach(mtcars)
qqnorm(mpg)
qqline(mpg)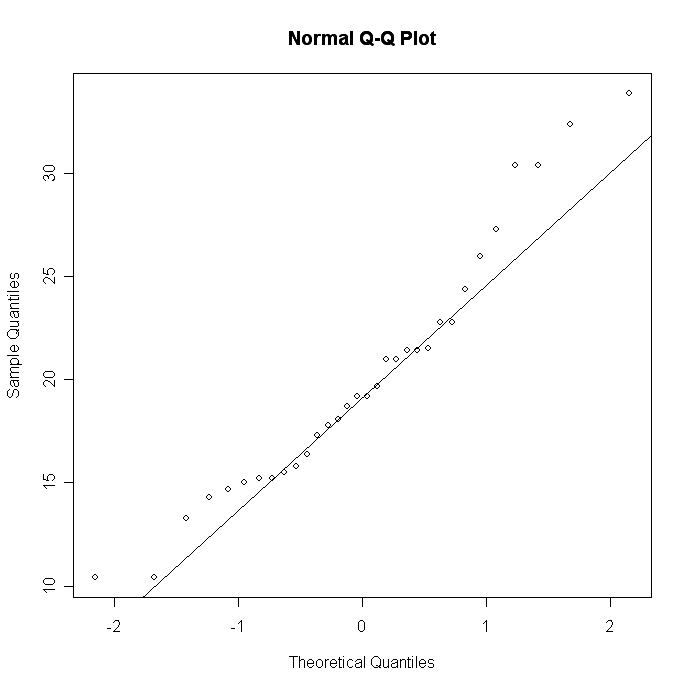

Las desviaciones significativas de la línea sugieren violaciones de la normalidad.

También puedes realizar una prueba de normalidad de Shapiro-Wilk con la función shapiro.test(x), donde x es un vector numérico. El paquete nortest</a > dispone de funciones adicionales para comprobar la normalidad.

Normalidad multivariante

El MANOVA asume la normalidad multivariante. La función mshapiro.test( ) del paquete mvnormtest</a > produce la prueba de Shapiro-Wilk para la normalidad multivariante. La entrada debe ser una matriz numérica.

# Test Multivariate Normality

mshapiro.test(M)

Si tenemos un vector aleatorio normal multivariante p x 1, la distancia de Mahalanobis al cuadrado entre x y μ tendrá una distribución chi-cuadrado con p grados de libertad. Podemos utilizar este hecho para construir un gráfico Q-Q para evaluar la normalidad multivariante.

# Graphical Assessment of Multivariate Normality
x <- as.matrix(mydata) # n x p numeric matrix
center <- colMeans(x) # centroid
n <- nrow(x); p <- ncol(x); cov <- cov(x);
d <-
mahalanobis(x,center,cov) # distances

qqplot(qchisq(ppoints(n),df=p),d,
  main="QQ Plot Assessing Multivariate Normality",
  ylab="Mahalanobis D2")
abline(a=0,b=1)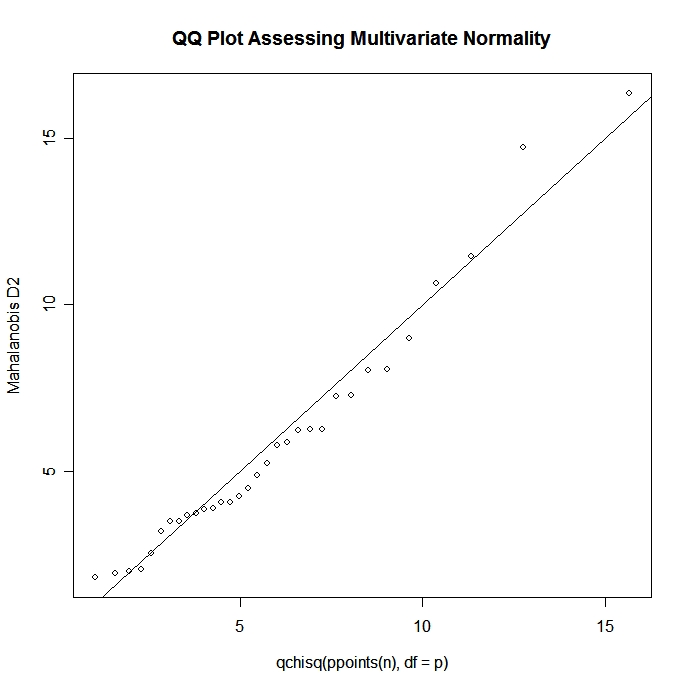

Homogeneidad de las varianzas

La función bartlett.test( ) proporciona una prueba paramétrica de muestras K de la igualdad de varianzas. La función fligner.test( ) proporciona una prueba no paramétrica de la misma. En los ejemplos siguientes y es una variable numérica y G es la variable de agrupación.

# Bartlett Test of Homogeneity of Variances
bartlett.test(y~G, data=mydata)

# Figner-Killeen Test of Homogeneity of Variances
fligner.test(y~G, data=mydata)

La función hovPlot( ) del paquete HH proporciona una prueba gráfica de homogeneidad de varianzas basada en Brown-Forsyth. En el siguiente ejemplo, y es numérico y G es un factor de agrupación. Ten en cuenta que G debe ser de tipo factor.

# Homogeneity of Variance Plot
library(HH)
hov(y~G, data=mydata)
hovPlot(y~G,data=mydata)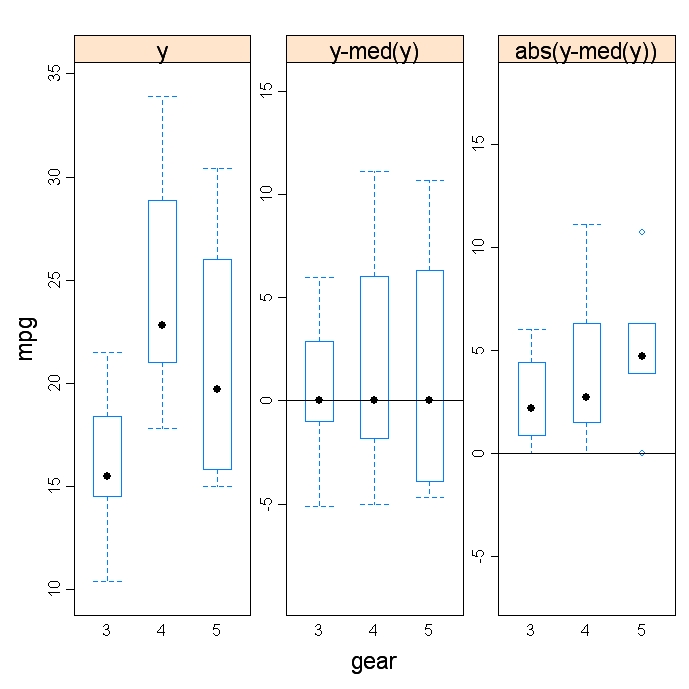

Homogeneidad de las matrices de covarianza

MANOVA y LDF suponen la homogeneidad de las matrices de varianza-covarianza. La hipótesis suele comprobarse con la M de Box. Desgraciadamente, la prueba es muy sensible a las violaciones de la normalidad, lo que conduce al rechazo en la mayoría de los casos típicos. La M de Box está disponible mediante la función boxM del paquete biotools</a > .

Practicar

Sigue el curso Introducción a la Estadística en R</a > para ampliar tus conocimientos estadísticos .