Análisis de conglomerados en R

R ofrece una amplia gama de funciones para análisis de conglomerados</a >, incluidos los enfoques jerárquico aglomerativo, de partición y basado en modelos. Aunque no existe una solución definitiva para determinar el número óptimo de conglomerados a extraer, hay varios enfoques disponibles.

Preparación de datos

Antes de agrupar los datos, quizá quieras eliminar o estimar los datos que faltan y reescalar las variables para que sean comparables.

# Prepare Data
mydata <- na.omit(mydata) # listwise deletion of missing
mydata <- scale(mydata) # standardize variables

Partición

La agrupación de K-means es el método de partición más popular. Requiere que el analista especifique el número de conglomerados a extraer. Un gráfico de la suma de cuadrados dentro de los grupos según el número de conglomerados extraídos puede ayudar a determinar el número adecuado de conglomerados. El analista busca una curvatura en el gráfico similar a la prueba scree en el análisis factorial.

# Determine number of clusters
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(mydata,
   centers=i)$withinss)
plot(1:15, wss, type="b", xlab="Number of Clusters",
  ylab="Within groups sum of squares")

# K-Means Cluster Analysis
fit <- kmeans(mydata, 5) # 5 cluster solution
# get cluster means
aggregate(mydata,by=list(fit$cluster),FUN=mean)
# append cluster assignment
mydata <- data.frame(mydata, fit$cluster)

Se puede invocar una versión robusta de K-means basada en mediods utilizando pam( ) en lugar de kmeans( ). La función pamk( ) del paquete fpc</a ></strong > es una envoltura de pam que también imprime el número sugerido de conglomerados basándose en la anchura media óptima de la silueta.

Aglomerativo jerárquico

Existe una amplia gama de enfoques de agrupación jerárquica. He tenido buena suerte con el método de Ward que se describe a continuación.

# Ward Hierarchical Clustering
d <- dist(mydata,
method = "euclidean") # distance matrix
fit <- hclust(d, method="ward")

plot(fit) # display dendogram
groups <- cutree(fit, k=5) # cut tree into 5 clusters
# draw dendogram with red borders around the 5 clusters
rect.hclust(fit, k=5, border="red")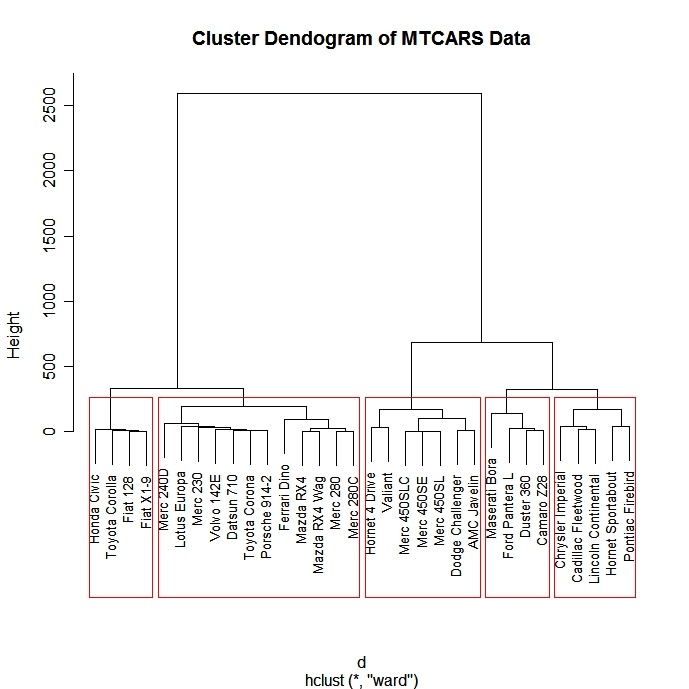

La función pvclust( ) del paquete pvclust</a > proporciona valores p para la agrupación jerárquica basada en el remuestreo bootstrap multiescala. Los conglomerados muy apoyados por los datos tendrán valores p grandes. Ten en cuenta que pvclust</a > agrupa columnas, no filas. Transpón tus datos antes de utilizarlos.

# Ward Hierarchical Clustering with Bootstrapped p values
library(pvclust)
fit <-
pvclust(mydata, method.hclust="ward",
   method.dist="euclidean")
plot(fit) # dendogram with p values
# add rectangles around groups highly supported by the data
pvrect(fit, alpha=.95)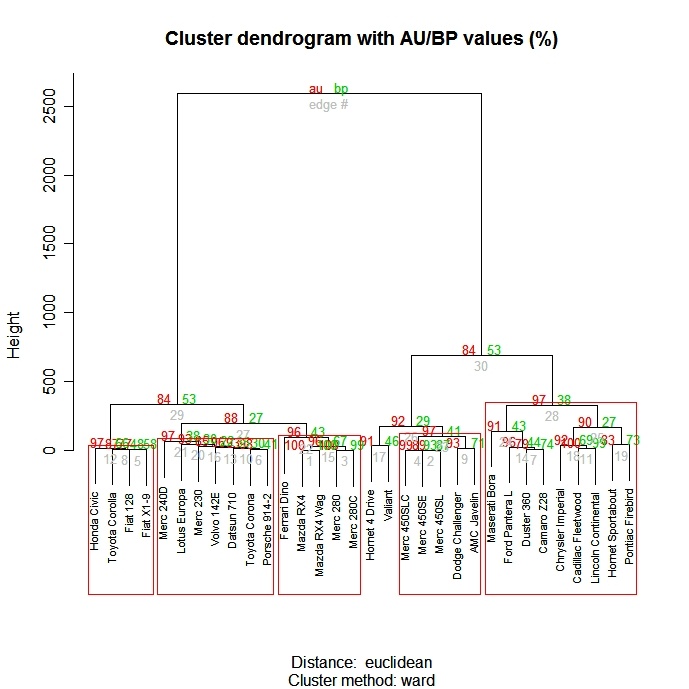

Basado en modelos

Los enfoques basados en modelos asumen una variedad de modelos de datos y aplican la estimación de máxima verosimilitud y los criterios de Bayes para identificar el modelo más probable y el número de conglomerados. En concreto, la función Mclust( ) del paquete mclust selecciona el modelo óptimo según el BIC para EM inicializado por agrupación jerárquica para modelos de mezcla gaussiana parametrizados. (¡uf!). Se elige el modelo y el número de conglomerados con el mayor BIC. Consulta help(mclustModelNames)</a > para conocer los detalles sobre el modelo elegido como mejor.

# Model Based Clustering
library(mclust)
fit <- Mclust(mydata)
plot(fit) # plot results

summary(fit) # display the best model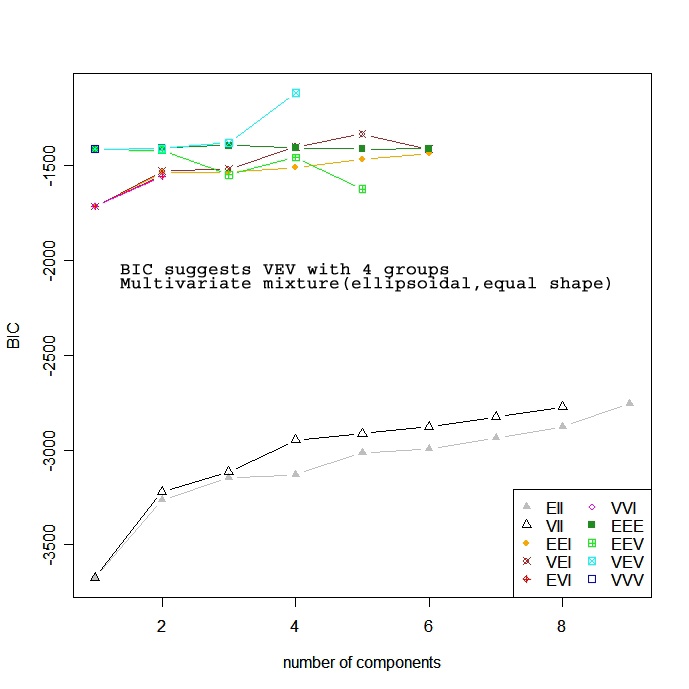

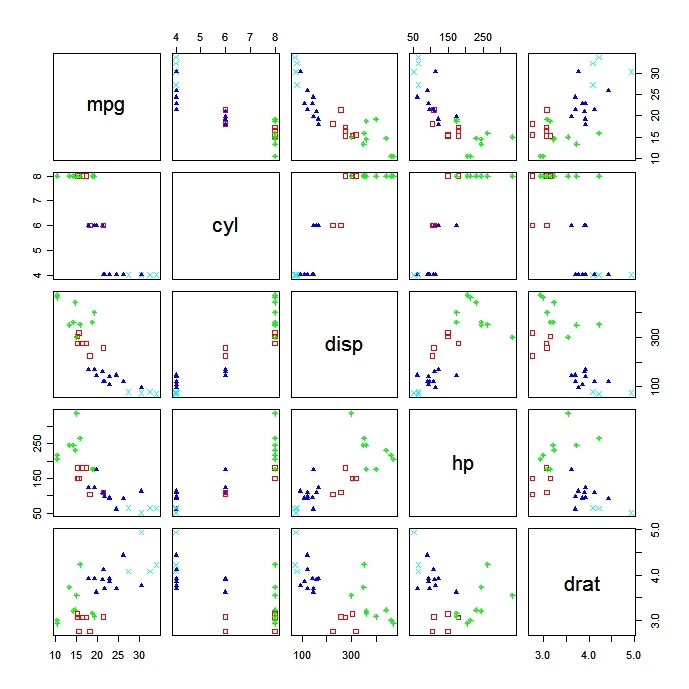
Trazado de soluciones de conglomerados

Siempre es una buena idea mirar los resultados del grupo.

# K-Means Clustering with 5 clusters
fit <- kmeans(mydata, 5)

# Cluster Plot against 1st 2 principal components

# vary parameters for most readable graph
library(cluster)

clusplot(mydata, fit$cluster, color=TRUE, shade=TRUE,
   labels=2, lines=0)

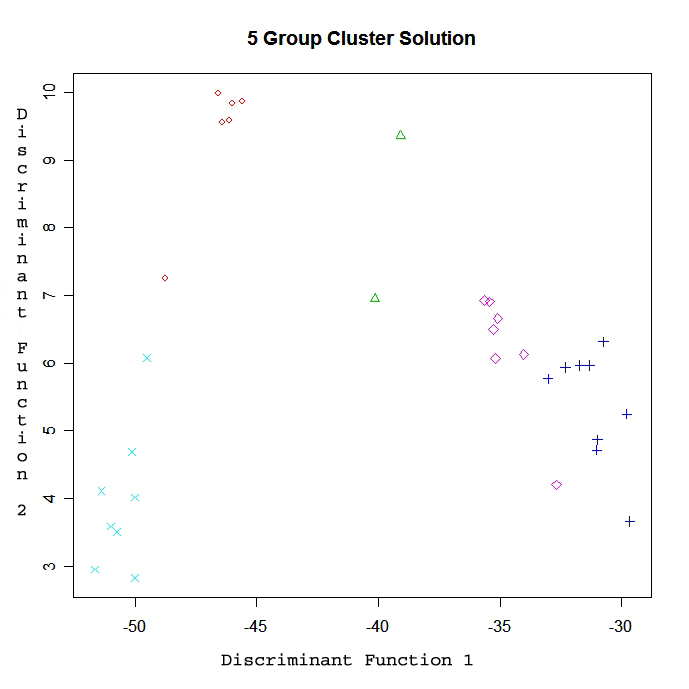
# Centroid Plot against 1st 2 discriminant functions
library(fpc)
plotcluster(mydata, fit$cluster)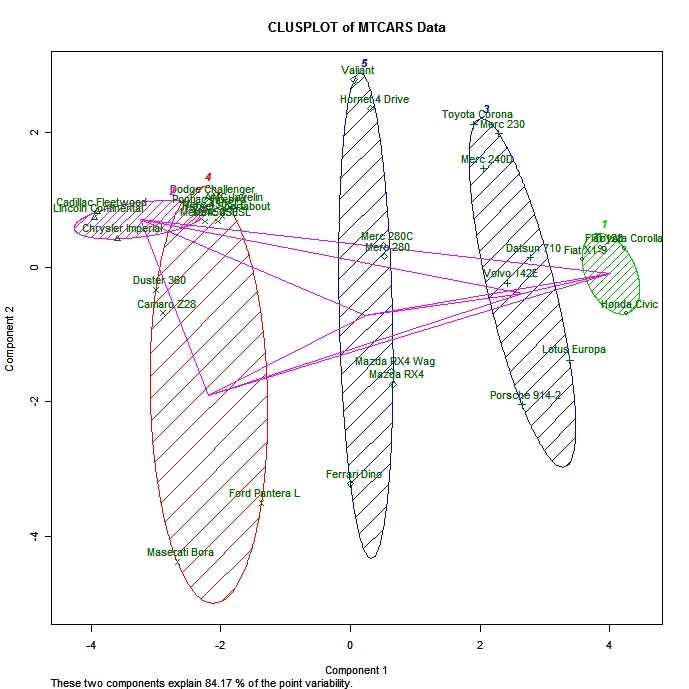

Validar las soluciones de clúster

La función cluster.stats() del paquete fpc proporciona un mecanismo para comparar la similitud de dos soluciones de conglomerados utilizando diversos criterios de validación (el coeficiente gamma de Hubert, el índice de Dunn y el índice rand corregido)

# comparing 2 cluster solutions
library(fpc)
cluster.stats(d, fit1$cluster, fit2$cluster)

donde d es una matriz de distancias entre objetos, y fit1$cluster y fit$cluste r son vectores enteros que contienen los resultados de la clasificación de dos agrupaciones diferentes de los mismos datos.

Practicar

Prueba el ejercicio de agrupación en este curso de introducción al aprendizaje automático.</a >