Componentes principales y análisis factorial en R

En esta sección se tratan los componentes principales y el análisis factorial. Este último incluye tanto métodos exploratorios como confirmatorios.

Componentes principales

La función princomp( ) produce un análisis de componentes principales sin rotar.

# Pricipal Components Analysis
# entering raw data and extracting PCs
#
from the correlation matrix

fit <- princomp(mydata, cor=TRUE)
summary(fit) # print variance accounted for
loadings(fit) # pc loadings
plot(fit,type="lines") # scree plot
fit$scores # the principal components
biplot(fit)

haz clic para ver

Utiliza cor=FALSE para basar los componentes principales en la matriz de covarianza. Utiliza la opción covmat= para introducir directamente una matriz de correlación o de covarianza. Si introduces una matriz de covarianza, incluye la opción n.obs=.

La función principal( ) del paquete psych puede utilizarse para extraer y rotar componentes principales.

# Varimax Rotated Principal Components
# retaining 5 components
library(psych)
fit <- principal(mydata, nfactors=5, rotate="varimax")
fit # print results

mydata puede ser una matriz de datos brutos o una matriz de covarianza. Se utiliza la eliminación por pares de los datos que faltan. rotar puede ser "ninguno", "varimax", "quatimax", "promax", "oblimin", "simplimax" o "cluster"

Análisis factorial exploratorio

La función factanal( ) produce análisis factoriales de máxima verosimilitud.

# Maximum Likelihood Factor Analysis
# entering raw data and extracting 3 factors,
#
with varimax rotation

fit <- factanal(mydata, 3, rotation="varimax")
print(fit, digits=2, cutoff=.3, sort=TRUE)
# plot factor 1 by factor 2
load <- fit$loadings[,1:2]
plot(load,type="n") # set up plot
text(load,labels=names(mydata),cex=.7) # add variable names

haz clic para ver

Las opciones de rotación= son "varimax", "promax" y "ninguna". Añade la opción puntuaciones="regresión" o "Bartlett" para obtener puntuaciones factoriales. Utiliza la opción covmat= para introducir directamente una matriz de correlación o de covarianza. Si introduces una matriz de covarianza, incluye la opción n.obs=.

La función factor.pa( ) del paquete psych ofrece una serie de funciones relacionadas con el análisis factorial, incluida la factorización del eje principal.

# Principal Axis Factor Analysis
library(psych)
fit <- factor.pa(mydata, nfactors=3, rotation="varimax")
fit # print results

mydata puede ser una matriz de datos brutos o una matriz de covarianza. Se utiliza la eliminación por pares de los datos que faltan. La rotación puede ser "varimax" o "promax".

Determinar el número de factores a extraer

Una decisión crucial en el análisis factorial exploratorio es cuántos factores extraer. El paqueteThenFactors ofrece un conjunto de funciones para ayudar en esta decisión. Puedes encontrar más detalles sobre esta metodología en una presentación en PowerPoint de Raiche, Riopel y Blais. Por supuesto, cualquier solución factorial debe ser interpretable para ser útil.

# Determine Number of Factors to Extract
library(nFactors)
ev <- eigen(cor(mydata)) # get eigenvalues
ap <- parallel(subject=nrow(mydata),var=ncol(mydata),
  rep=100,cent=.05)
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea)
plotnScree(nS)

haz clic para ver

Ir más lejos

El paqueteFactoMineR ofrece un gran número de funciones adicionales para el análisis factorial exploratorio. Esto incluye el uso de variables cuantitativas y cualitativas, así como la inclusión de variables y observaciones complementarias. Aquí tienes un ejemplo de los tipos de gráficos que puedes crear con este paquete.

# PCA Variable Factor Map
library(FactoMineR)
result <- PCA(mydata) # graphs generated automatically

haz clic para ver

El paquete GPARotation ofrece una gran variedad de opciones de rotación, además de varimax y promax.

Modelización de ecuaciones estructurales

El Análisis Factorial Confirmatorio (AFC) es un subconjunto de la metodología mucho más amplia del Modelado de Ecuaciones Estructurales (SEM). El SEM se proporciona en R mediante el paquete sem. Los modelos se introducen mediante la especificación RAM (similar a PROC CALIS en SAS). Aunque Sem es un paquete completo, mi recomendación es que, si realizas un trabajo SEM importante, te hagas con una copia de AMOS. Puede ser mucho más fácil de usar y crea resultados más atractivos y listos para publicar. Dicho esto, aquí tienes un ejemplo de CFA utilizando sem.

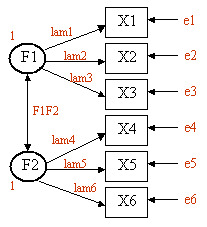
Supongamos que tenemos seis variables observadas (X1, X2, ..., X6). Nuestra hipótesis es que existen dos factores latentes no observados (F1, F2) que subyacen a las variables observadas, como se describe en este diagrama. X1, X2 y X3 cargan sobre F1 (con cargas lam1, lam2 y lam3). X4, X5 y X6 cargan en F2 (con cargas lam4, lam5 y lam6). La flecha de doble punta indica la covarianza entre los dos factores latentes (F1F2). e1 a e6 representan las varianzas residuales (varianza en las variables observadas no explicada por los dos factores latentes). Establecemos las varianzas de F1 y F2 iguales a uno para que los parámetros tengan una escala. El resultado será F1F2, que representa la correlación entre los dos factores latentes.

Para sem, necesitamos la matriz de covarianza de las variables observadas - de ahí la sentencia cov( ) del código siguiente. El modelo CFA se especifica mediante la función especificar.modelo( ). El formato es especificación de flecha, nombre del parámetro, valor inicial. Elegir un valor inicial de NA indica al programa que elija un valor inicial en lugar de proporcionarlo tú mismo. Observa que la varianza de F1 y F2 se fija en 1 (NA en la segunda columna). La línea en blanco es necesaria para finalizar la especificación RAM.

# Simple CFA Model
library(sem)
mydata.cov <- cov(mydata)
model.mydata <- specify.model()
F1 ->  X1, lam1, NA
F1 ->  X2, lam2, NA
F1 ->  X3, lam3, NA
F2 ->  X4, lam4, NA
F2 ->  X5, lam5, NA
F2 ->  X6, lam6, NA
X1 <-> X1, e1,   NA
X2 <-> X2, e2,   NA
X3 <-> X3, e3,   NA
X4 <-> X4, e4,   NA
X5 <-> X5, e5,   NA
X6 <-> X6, e6,   NA
F1 <-> F1, NA,    1
F2 <-> F2, NA,    1
F1 <-> F2, F1F2, NA

mydata.sem <- sem(model.mydata, mydata.cov, nrow(mydata))
# print results (fit indices, paramters, hypothesis tests)
summary(mydata.sem)
# print standardized coefficients (loadings)

std.coef(mydata.sem)

Puedes utilizar la función boot.sem( ) para hacer un bootstrap del modelo de ecuación estructural. Consulta help(boot.sem) para más detalles. Además, la función mod.indices( ) producirá índices de modificación. Utilizar índices de modificación para mejorar el ajuste del modelo reespecificando los parámetros te hace pasar de un análisis confirmatorio a uno exploratorio.

Para obtener más información sobre sem, consulta Structural Equation Modeling with the sem Package in R, de John Fox.

Practicar

Para practicar la mejora de las predicciones, prueba el curso Aprendizaje supervisado en R