Clusteranalyse in R

R bietet eine breite Palette von Funktionen für die Clusteranalyse</a >, darunter hierarchische agglomerative, partitionierende und modellbasierte Ansätze. Obwohl es keine endgültige Lösung für die Bestimmung der optimalen Anzahl von Clustern gibt, die extrahiert werden sollen, gibt es verschiedene Ansätze.

Datenaufbereitung

Bevor du Daten clusterst, solltest du fehlende Daten entfernen oder schätzen und Variablen neu skalieren, um sie vergleichbar zu machen.

# Prepare Data
mydata <- na.omit(mydata) # listwise deletion of missing
mydata <- scale(mydata) # standardize variables

Partitioning

Das K-Mittel-Clustering ist die beliebteste Partitionierungsmethode. Dabei muss der Analyst die Anzahl der zu extrahierenden Cluster angeben. Eine Darstellung der Summe der Quadrate innerhalb der Gruppen nach der Anzahl der extrahierten Cluster kann helfen, die geeignete Anzahl von Clustern zu bestimmen. Der Analyst sucht nach einem Knick im Diagramm, ähnlich wie bei einem Scree-Test in der Faktorenanalyse.

# Determine number of clusters
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(mydata,
   centers=i)$withinss)
plot(1:15, wss, type="b", xlab="Number of Clusters",
  ylab="Within groups sum of squares")

# K-Means Cluster Analysis
fit <- kmeans(mydata, 5) # 5 cluster solution
# get cluster means
aggregate(mydata,by=list(fit$cluster),FUN=mean)
# append cluster assignment
mydata <- data.frame(mydata, fit$cluster)

Eine robuste Version von K-means, die auf Mediods basiert, kann durch die Verwendung von pam( ) anstelle von kmeans( ) aufgerufen werden. Die Funktion pamk( ) aus dem fpc</a ></strong > Paket ist ein Wrapper für pam, der auch die vorgeschlagene Anzahl von Clustern basierend auf der optimalen durchschnittlichen Silhouettenbreite ausgibt.

Hierarchisch Agglomerativ

Es gibt eine ganze Reihe von hierarchischen Clustering-Ansätzen. Ich habe gute Erfahrungen mit der unten beschriebenen Methode von Ward gemacht.

# Ward Hierarchical Clustering
d <- dist(mydata,
method = "euclidean") # distance matrix
fit <- hclust(d, method="ward")

plot(fit) # display dendogram
groups <- cutree(fit, k=5) # cut tree into 5 clusters
# draw dendogram with red borders around the 5 clusters
rect.hclust(fit, k=5, border="red")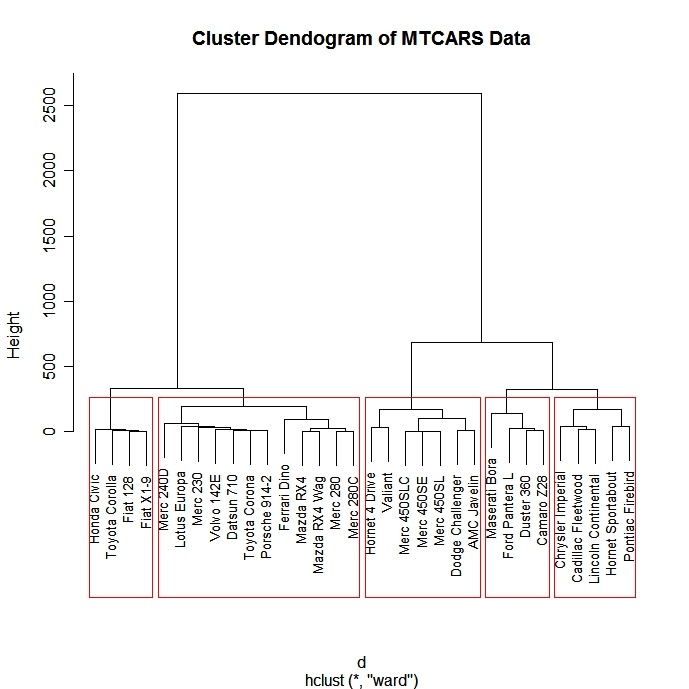

Die Funktion pvclust( ) im Paket pvclust</a > liefert p-Werte für hierarchisches Clustering auf der Grundlage von multiskaligen Bootstrap-Resampling. Cluster, die von den Daten stark unterstützt werden, haben große p-Werte. Beachte, dass pvclust</a > Spalten clustert, nicht Zeilen. Transponiere deine Daten vor der Verwendung.

# Ward Hierarchical Clustering with Bootstrapped p values
library(pvclust)
fit <-
pvclust(mydata, method.hclust="ward",
   method.dist="euclidean")
plot(fit) # dendogram with p values
# add rectangles around groups highly supported by the data
pvrect(fit, alpha=.95)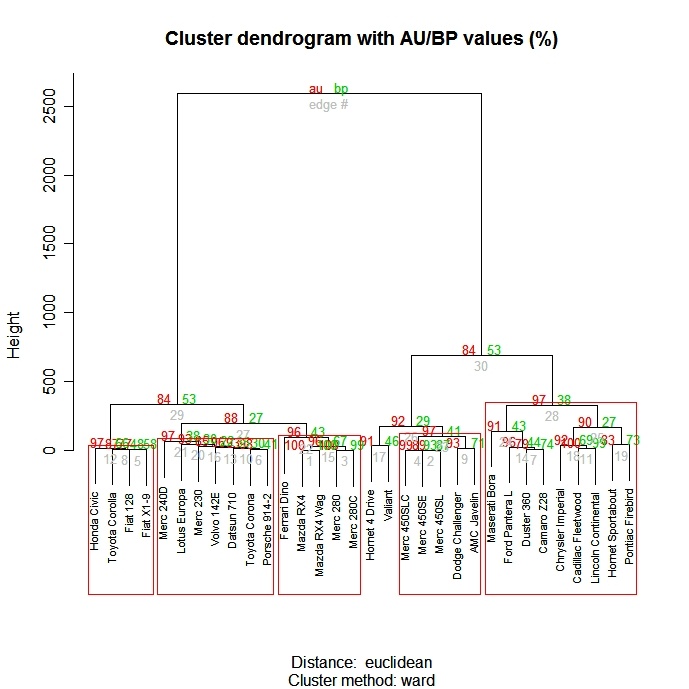

Modellbasiert

Modellbasierte Ansätze gehen von einer Vielzahl von Datenmodellen aus und verwenden Maximum-Likelihood-Schätzungen und Bayes-Kriterien, um das wahrscheinlichste Modell und die Anzahl der Cluster zu ermitteln. Konkret wählt die Funktion Mclust( ) im Paket mclust das optimale Modell nach BIC für EM aus, das durch hierarchisches Clustering für parametrisierte Gaußsche Mischungsmodelle initialisiert wird. (puh!). Man wählt das Modell und die Anzahl der Cluster mit dem größten BIC. Siehe help(mclustModelNames)</a > für Details zu dem Modell, das als bestes ausgewählt wurde.

# Model Based Clustering
library(mclust)
fit <- Mclust(mydata)
plot(fit) # plot results

summary(fit) # display the best model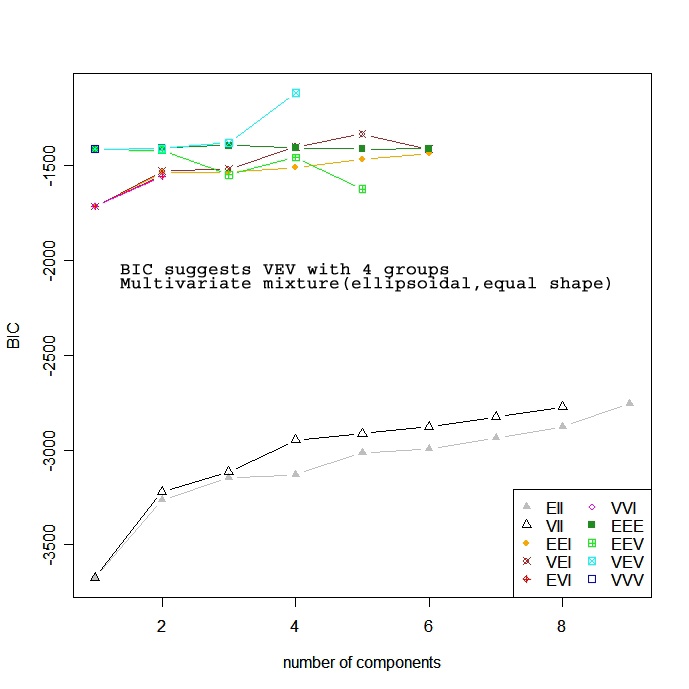

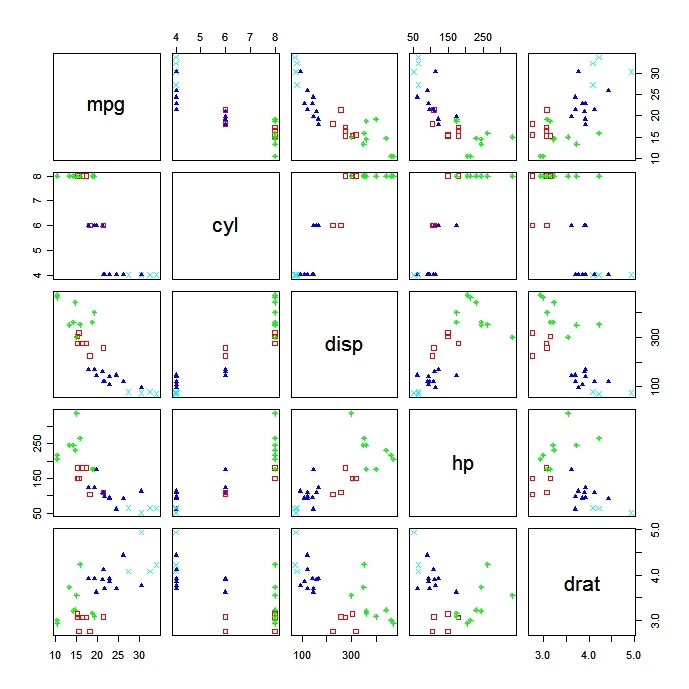
Plotten von Clusterlösungen

Es ist immer eine gute Idee, sich die Ergebnisse des Clusters anzusehen.

# K-Means Clustering with 5 clusters
fit <- kmeans(mydata, 5)

# Cluster Plot against 1st 2 principal components

# vary parameters for most readable graph
library(cluster)

clusplot(mydata, fit$cluster, color=TRUE, shade=TRUE,
   labels=2, lines=0)

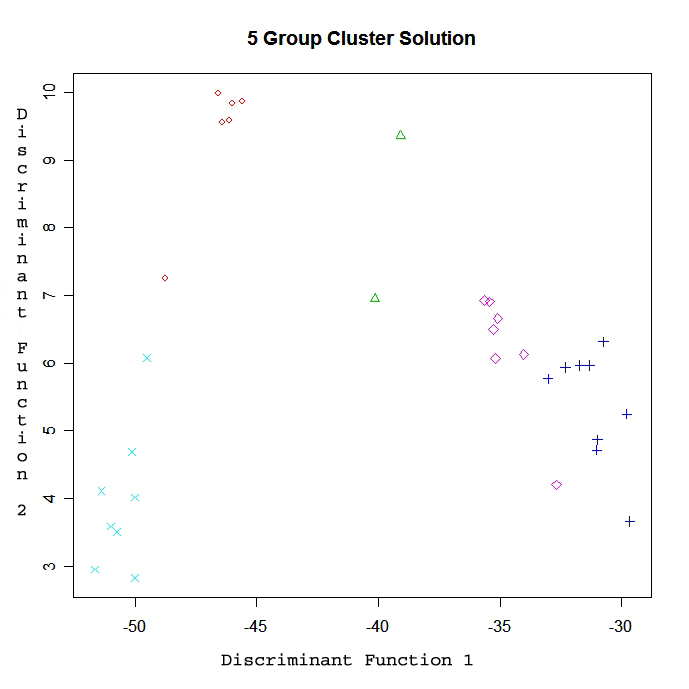
# Centroid Plot against 1st 2 discriminant functions
library(fpc)
plotcluster(mydata, fit$cluster)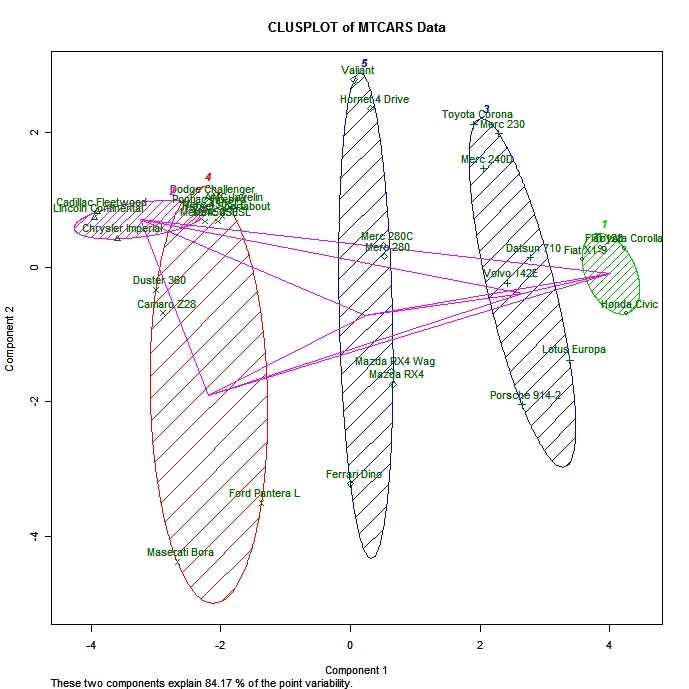

Validierung von Cluster-Lösungen

Die Funktion cluster.stats() im fpc-Paket bietet einen Mechanismus zum Vergleich der Ähnlichkeit zweier Clusterlösungen anhand verschiedener Validierungskriterien (Hubert's Gamma-Koeffizient, Dunn-Index und korrigierter Rand-Index)

# comparing 2 cluster solutions
library(fpc)
cluster.stats(d, fit1$cluster, fit2$cluster)

Dabei ist d eine Abstandsmatrix zwischen den Objekten und fit1$cluster und fit$cluste r sind ganzzahlige Vektoren, die Klassifizierungsergebnisse aus zwei verschiedenen Clustern derselben Daten enthalten.

Zum Üben

Versuche die Clustering-Übung in diesem Kurs zur Einführung in das maschinelle Lernen.</a >