Composantes principales et analyse factorielle dans R

Cette section traite des composantes principales et de l'analyse factorielle. Cette dernière comprend à la fois des méthodes exploratoires et des méthodes confirmatoires.

Composantes principales

La fonction princomp( ) produit une analyse en composantes principales non tournée.

# Pricipal Components Analysis
# entering raw data and extracting PCs
#
from the correlation matrix

fit <- princomp(mydata, cor=TRUE)
summary(fit) # print variance accounted for
loadings(fit) # pc loadings
plot(fit,type="lines") # scree plot
fit$scores # the principal components
biplot(fit)

cliquez pour voir

Utilisez cor=FALSE pour baser les composantes principales sur la matrice de covariance. Utilisez l'option covmat= pour saisir directement une matrice de corrélation ou de covariance. Si vous entrez une matrice de covariance, incluez l'option n.obs=.

La fonction principal( ) du paquet psych peut être utilisée pour extraire et faire pivoter les composantes principales.

# Varimax Rotated Principal Components
# retaining 5 components
library(psych)
fit <- principal(mydata, nfactors=5, rotate="varimax")
fit # print results

mydata peut être une matrice de données brutes ou une matrice de covariance. La suppression par paire des données manquantes est utilisée. La rotation peut être "none", "varimax", "quatimax", "promax", "oblimin", "simplimax" ou "cluster".

Analyse factorielle exploratoire

La fonction factanal( ) produit une analyse factorielle du maximum de vraisemblance.

# Maximum Likelihood Factor Analysis
# entering raw data and extracting 3 factors,
#
with varimax rotation

fit <- factanal(mydata, 3, rotation="varimax")
print(fit, digits=2, cutoff=.3, sort=TRUE)
# plot factor 1 by factor 2
load <- fit$loadings[,1:2]
plot(load,type="n") # set up plot
text(load,labels=names(mydata),cex=.7) # add variable names

cliquez pour voir

Les options de rotation= comprennent "varimax", "promax" et "none". Ajoutez l'option scores="regression" ou "Bartlett" pour produire des scores factoriels. Utilisez l'option covmat= pour saisir directement une matrice de corrélation ou de covariance. Si vous entrez une matrice de covariance, incluez l'option n.obs=.

La fonction factor.pa( ) du paquet psych offre un certain nombre de fonctions liées à l'analyse factorielle, y compris la factorisation de l'axe principal.

# Principal Axis Factor Analysis
library(psych)
fit <- factor.pa(mydata, nfactors=3, rotation="varimax")
fit # print results

mydata peut être une matrice de données brutes ou une matrice de covariance. Les données manquantes sont supprimées par paire. La rotation peut être "varimax" ou "promax".

Déterminer le nombre de facteurs à extraire

Une décision cruciale dans l'analyse factorielle exploratoire est le nombre de facteurs à extraire. Le progicielThenFactors offre une série de fonctions pour vous aider à prendre cette décision. Vous trouverez des détails sur cette méthodologie dans une présentation PowerPoint de Raiche, Riopel et Blais. Bien entendu, pour être utile, toute solution factorielle doit pouvoir être interprétée.

# Determine Number of Factors to Extract
library(nFactors)
ev <- eigen(cor(mydata)) # get eigenvalues
ap <- parallel(subject=nrow(mydata),var=ncol(mydata),
  rep=100,cent=.05)
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea)
plotnScree(nS)

cliquez pour voir

Aller plus loin

Le paquetageFactoMineR offre un grand nombre de fonctions supplémentaires pour l'analyse factorielle exploratoire. Cela comprend l'utilisation de variables quantitatives et qualitatives, ainsi que l'inclusion de variables complémentaires et d'observations. Voici un exemple des types de graphiques que vous pouvez créer avec ce logiciel.

# PCA Variable Factor Map
library(FactoMineR)
result <- PCA(mydata) # graphs generated automatically

cliquez pour voir

Le package GPARotation offre une multitude d'options de rotation au-delà de varimax et promax.

Modélisation des équations structurelles

L'analyse factorielle confirmatoire (AFC) est un sous-ensemble de la méthodologie beaucoup plus large de la modélisation par équations structurelles (SEM). Le SEM est fourni dans R via le package sem. Les modèles sont introduits via la spécification RAM (similaire à PROC CALIS dans SAS). Bien que sem soit un logiciel complet, je vous recommande d'acheter une copie d'AMOS si vous effectuez un travail important dans le domaine du SEM. Elle peut être beaucoup plus conviviale et produire des résultats plus attrayants et prêts à être publiés. Cela dit, voici un exemple de CFA utilisant des sem.

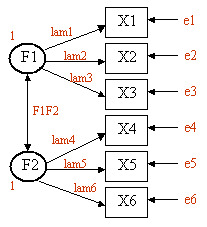
Supposons que nous ayons six variables observées (X1, X2, ..., X6). Nous supposons qu'il existe deux facteurs latents non observés (F1, F2) qui sous-tendent les variables observées, comme décrit dans ce diagramme. X1, X2 et X3 se chargent de F1 (avec les charges lam1, lam2 et lam3). X4, X5 et X6 se chargent sur F2 (avec les charges lam4, lam5 et lam6). La flèche à deux têtes indique la covariance entre les deux facteurs latents (F1F2). e1 à e6 représentent les variances résiduelles (variance des variables observées non prise en compte par les deux facteurs latents). Nous fixons les variances de F1 et F2 égales à un afin que les paramètres aient une échelle. Il en résulte que F1F2 représente la corrélation entre les deux facteurs latents.

Pour sem, nous avons besoin de la matrice de covariance des variables observées - d'où l'instruction cov( ) dans le code ci-dessous. Le modèle CFA est spécifié à l'aide de la fonction specify.model( ). Le format est le suivant : spécification de la flèche, nom du paramètre, valeur de départ. Le choix d'une valeur de départ de NA indique au programme de choisir une valeur de départ plutôt que d'en fournir une vous-même. Notez que la variance de F1 et F2 est fixée à 1 (NA dans la deuxième colonne). La ligne vierge est nécessaire pour terminer la spécification de la RAM.

# Simple CFA Model
library(sem)
mydata.cov <- cov(mydata)
model.mydata <- specify.model()
F1 ->  X1, lam1, NA
F1 ->  X2, lam2, NA
F1 ->  X3, lam3, NA
F2 ->  X4, lam4, NA
F2 ->  X5, lam5, NA
F2 ->  X6, lam6, NA
X1 <-> X1, e1,   NA
X2 <-> X2, e2,   NA
X3 <-> X3, e3,   NA
X4 <-> X4, e4,   NA
X5 <-> X5, e5,   NA
X6 <-> X6, e6,   NA
F1 <-> F1, NA,    1
F2 <-> F2, NA,    1
F1 <-> F2, F1F2, NA

mydata.sem <- sem(model.mydata, mydata.cov, nrow(mydata))
# print results (fit indices, paramters, hypothesis tests)
summary(mydata.sem)
# print standardized coefficients (loadings)

std.coef(mydata.sem)

Vous pouvez utiliser la fonction boot.sem( ) pour amorcer le modèle d'équation structurelle. Voir help(boot.sem) pour plus de détails. En outre, la fonction mod.indices( ) produit des indices de modification. L'utilisation d'indices de modification pour améliorer l'adéquation du modèle en respécifiant les paramètres vous fait passer d'une analyse confirmatoire à une analyse exploratoire.

Pour plus d'informations sur sem, voir Structural Equation Modeling with the sem Package in R, par John Fox.

Pratiquer

Pour vous entraîner à améliorer les prédictions, essayez le cours Apprentissage supervisé en R