Hauptkomponenten und Faktorenanalyse in R

Dieser Abschnitt behandelt die Hauptkomponenten und die Faktorenanalyse. Letzteres umfasst sowohl explorative als auch konfirmatorische Methoden.

Hauptkomponenten

Die Funktion princomp( ) erstellt eine ungedrehte Hauptkomponentenanalyse.

# Pricipal Components Analysis
# entering raw data and extracting PCs
#
from the correlation matrix

fit <- princomp(mydata, cor=TRUE)
summary(fit) # print variance accounted for
loadings(fit) # pc loadings
plot(fit,type="lines") # scree plot
fit$scores # the principal components
biplot(fit)

Zur Ansicht klicken

Verwende cor=FALSE, um die Hauptkomponenten auf die Kovarianzmatrix zu stützen. Verwende die Option covmat=, um eine Korrelations- oder Kovarianzmatrix direkt einzugeben. Wenn du eine Kovarianzmatrix eingibst, gib die Option n.obs= an .

Mit der Funktion principal( ) im psych-Paket kannst du die Hauptkomponenten extrahieren und rotieren.

# Varimax Rotated Principal Components
# retaining 5 components
library(psych)
fit <- principal(mydata, nfactors=5, rotate="varimax")
fit # print results

mydata kann eine Rohdatenmatrix oder eine Kovarianzmatrix sein. Paarweise Löschung von fehlenden Daten wird verwendet. rotate kann "none", "varimax", "quatimax", "promax", "oblimin", "simplimax" oder "cluster" sein

Explorative Faktorenanalyse

Die Funktion factanal( ) erstellt eine Maximum-Likelihood-Faktoranalyse.

# Maximum Likelihood Factor Analysis
# entering raw data and extracting 3 factors,
#
with varimax rotation

fit <- factanal(mydata, 3, rotation="varimax")
print(fit, digits=2, cutoff=.3, sort=TRUE)
# plot factor 1 by factor 2
load <- fit$loadings[,1:2]
plot(load,type="n") # set up plot
text(load,labels=names(mydata),cex=.7) # add variable names

Zur Ansicht klicken

Die Optionen für rotation= sind "varimax", "promax" und "none". Füge die Option scores="regression" oder "Bartlett" hinzu, um Faktorwerte zu erhalten. Verwende die Option covmat=, um eine Korrelations- oder Kovarianzmatrix direkt einzugeben. Wenn du eine Kovarianzmatrix eingibst, gib die Option n.obs= an .

Die Funktion factor.pa( ) im Paket psych bietet eine Reihe von Funktionen für die Faktorenanalyse, darunter auch das Factoring der Hauptachsen.

# Principal Axis Factor Analysis
library(psych)
fit <- factor.pa(mydata, nfactors=3, rotation="varimax")
fit # print results

mydata kann eine Rohdatenmatrix oder eine Kovarianzmatrix sein. Die fehlenden Daten werden paarweise gelöscht. Die Rotation kann "varimax" oder "promax" sein.

Festlegen der Anzahl der zu extrahierenden Faktoren

Eine wichtige Entscheidung bei der explorativen Faktorenanalyse ist, wie viele Faktoren extrahiert werden sollen. DasThenFactors-Paket bietet eine Reihe von Funktionen, die dir bei dieser Entscheidung helfen. Einzelheiten zu dieser Methodik findest du in einer PowerPoint-Präsentation von Raiche, Riopel und Blais. Natürlich muss jede Faktorlösung interpretierbar sein, um nützlich zu sein.

# Determine Number of Factors to Extract
library(nFactors)
ev <- eigen(cor(mydata)) # get eigenvalues
ap <- parallel(subject=nrow(mydata),var=ncol(mydata),
  rep=100,cent=.05)
nS <- nScree(x=ev$values, aparallel=ap$eigen$qevpea)
plotnScree(nS)

Zur Ansicht klicken

Weiter gehen

DasFactoMineR -Paket bietet eine große Anzahl zusätzlicher Funktionen für die explorative Faktorenanalyse. Dazu gehört die Verwendung sowohl quantitativer als auch qualitativer Variablen sowie die Einbeziehung von ergänzenden Variablen und Beobachtungen. Hier ist ein Beispiel für die Arten von Diagrammen, die du mit diesem Paket erstellen kannst.

# PCA Variable Factor Map
library(FactoMineR)
result <- PCA(mydata) # graphs generated automatically

Zur Ansicht klicken

Das GPARotation-Paket bietet eine Vielzahl von Rotationsoptionen, die über Varimax und Promax hinausgehen.

Strukturgleichungsmodellierung

Die konfirmatorische Faktorenanalyse ( Confirmatory Factor Analysis , CFA) ist eine Teilmenge der viel umfassenderen Methode der Strukturgleichungsmodellierung ( Structural Equation Modeling , SEM). SEM wird in R über das Paket sem bereitgestellt. Modelle werden über eine RAM-Spezifikation eingegeben (ähnlich wie PROC CALIS in SAS). Obwohl Sem ein umfassendes Paket ist, empfehle ich, dass du dir eine Kopie von AMOS zulegst, wenn du viel mit SEM arbeitest. Sie kann viel benutzerfreundlicher sein und erzeugt eine attraktivere und veröffentlichungsreife Ausgabe. Hier ist ein CFA-Beispiel mit Sem.

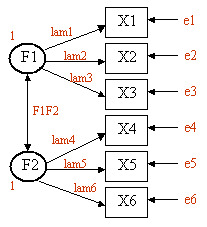
Nehmen wir an, wir haben sechs beobachtete Variablen (X1, X2, ..., X6). Wir stellen die Hypothese auf, dass es zwei unbeobachtete latente Faktoren (F1, F2) gibt, die den beobachteten Variablen zugrunde liegen, wie in diesem Diagramm beschrieben. X1, X2 und X3 lasten auf F1 (mit den Ladungen lam1, lam2 und lam3). X4, X5 und X6 lasten auf F2 (mit den Lasten lam4, lam5 und lam6). Der Doppelpfeil zeigt die Kovarianz zwischen den beiden latenten Faktoren (F1F2) an. e1 bis e6 stehen für die Restvarianzen (Varianz in den beobachteten Variablen, die nicht durch die beiden latenten Faktoren erklärt werden). Wir setzen die Varianzen von F1 und F2 gleich eins, damit die Parameter eine Skala haben. Das Ergebnis ist F1F2, das die Korrelation zwischen den beiden latenten Faktoren darstellt.

Für sem benötigen wir die Kovarianzmatrix der beobachteten Variablen - daher die cov( )-Anweisung im folgenden Code. Das CFA-Modell wird mit der Funktion specify.model( ) festgelegt. Das Format ist Pfeilangabe, Parametername, Startwert. Wenn du den Startwert NA auswählst, wird das Programm aufgefordert, einen Startwert zu wählen, anstatt ihn selbst anzugeben. Beachte, dass die Varianz von F1 und F2 auf 1 festgelegt ist (NA in der zweiten Spalte). Die Leerzeile ist erforderlich, um die RAM-Angabe zu beenden.

# Simple CFA Model
library(sem)
mydata.cov <- cov(mydata)
model.mydata <- specify.model()
F1 ->  X1, lam1, NA
F1 ->  X2, lam2, NA
F1 ->  X3, lam3, NA
F2 ->  X4, lam4, NA
F2 ->  X5, lam5, NA
F2 ->  X6, lam6, NA
X1 <-> X1, e1,   NA
X2 <-> X2, e2,   NA
X3 <-> X3, e3,   NA
X4 <-> X4, e4,   NA
X5 <-> X5, e5,   NA
X6 <-> X6, e6,   NA
F1 <-> F1, NA,    1
F2 <-> F2, NA,    1
F1 <-> F2, F1F2, NA

mydata.sem <- sem(model.mydata, mydata.cov, nrow(mydata))
# print results (fit indices, paramters, hypothesis tests)
summary(mydata.sem)
# print standardized coefficients (loadings)

std.coef(mydata.sem)

Du kannst die Funktion boot.sem( ) verwenden, um das Strukturgleichungsmodell zu booten. Siehe help(boot.sem) für Details. Außerdem erzeugt die Funktion mod.indices( ) Änderungsindizes. Wenn du Änderungsindizes verwendest, um die Modellanpassung durch eine Anpassung der Parameter zu verbessern, gehst du von einer konfirmatorischen zu einer exploratorischen Analyse über.

Weitere Informationen zu sem findest du in Structural Equation Modeling with the sem Package in R, von John Fox.

Zum Üben

Um die Verbesserung von Vorhersagen zu üben, probiere den Kurs "Überwachtes Lernen in R" aus