Multiple (lineare) Regression in R

R bietet umfassende Unterstützung für die multiple lineare Regression. Die folgenden Themen sind in der Reihenfolge ihrer zunehmenden Komplexität aufgeführt.

Anpassen des Modells

# Multiple Linear Regression Example

fit <- lm(y ~ x1 + x2 + x3, data=mydata)
summary(fit) # show results

# Other useful functions
coefficients(fit) # model coefficients
confint(fit, level=0.95) # CIs for model parameters

fitted(fit) # predicted values
residuals(fit) # residuals
anova(fit) # anova table
vcov(fit) # covariance matrix for model parameters
influence(fit) # regression diagnostics

Diagnostische Plots

Diagnostische Diagramme bieten Prüfungen auf Heteroskedastizität, Normalität und einflussreiche Beobachtungen.

# diagnostic plots
layout(matrix(c(1,2,3,4),2,2)) # optional 4 graphs/page
plot(fit)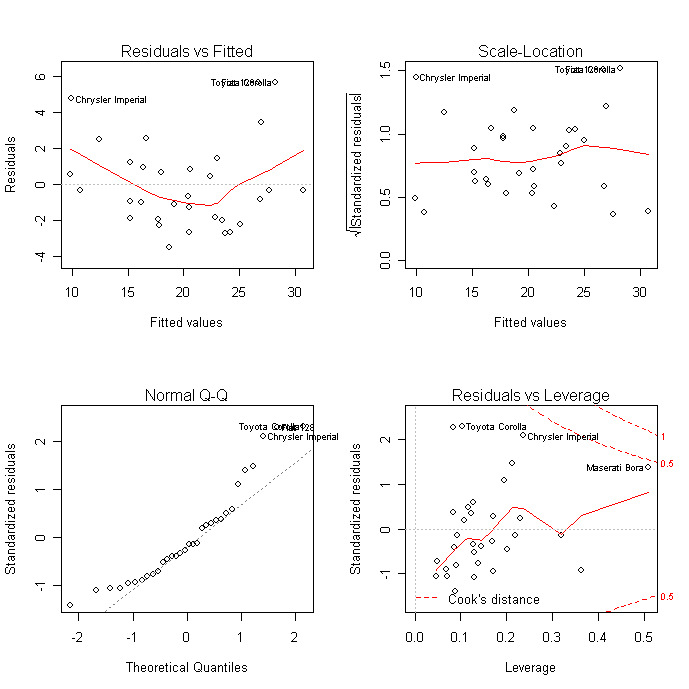

Eine umfassendere Bewertung der Modellanpassung findest du in der Regressionsdiagnose oder in den Übungen in diesem interaktiven Kurs</a > über Überwachtes Lernen in R: Regression.

Modelle im Vergleich

Du kannst verschachtelte Modelle mit der Funktion anova( ) vergleichen. Mit dem folgenden Code kannst du gleichzeitig prüfen, ob x3 und x4 über x1 und x2 hinaus zur linearen Vorhersage beitragen.

# compare models
fit1 <- lm(y ~ x1 + x2 + x3 + x4, data=mydata)
fit2 <- lm(y ~ x1 + x2)
anova(fit1, fit2)

Kreuzvalidierung

Du kannst die K-Fold-Kreuzvalidierung</a >mit der Funktion cv.lm( ) aus dem DAAG-Paket durchführen.

# K-fold cross-validation
library(DAAG)
cv.lm(df=mydata, fit, m=3) # 3 fold cross-validation

Addiere den MSE für jeden Fold, teile ihn durch die Anzahl der Beobachtungen und ziehe die Quadratwurzel, um den kreuzvalidierten Standardfehler der Schätzung zu erhalten.

Du kannst die R2-Schrumpfung durch K-fache Kreuzvalidierung bewerten. Verwende die Funktion crossval() aus dem bootstrap</a ></strong >-Paketes tust du Folgendes:

# Assessing R2 shrinkage using 10-Fold Cross-Validation

fit <- lm(y~x1+x2+x3,data=mydata)

library(bootstrap)
# define functions
theta.fit <- function(x,y){lsfit(x,y)}
theta.predict <- function(fit,x){cbind(1,x)%*%fit$coef}

# matrix of predictors
X
<- as.matrix(mydata[c("x1","x2","x3")])
# vector of predicted values
y <- as.matrix(mydata[c("y")])

results <- crossval(X,y,theta.fit,theta.predict,ngroup=10)
cor(y, fit$fitted.values)**2 # raw R2
cor(y,results$cv.fit)**2 # cross-validated R2

Variable Auswahl

Die Auswahl einer Teilmenge von Prädiktorvariablen aus einer größeren Menge (z. B. die schrittweise Auswahl) ist ein kontroverses Thema. Mit der Funktion stepAIC( ) aus dem MASS-Paket kannst du eine schrittweise Auswahl (vorwärts, rückwärts, beides) durchführen. stepAIC( ) führt eine schrittweise Modellauswahl durch exakten AIC durch.

# Stepwise Regression
library(MASS)
fit <- lm(y~x1+x2+x3,data=mydata)
step <- stepAIC(fit, direction="both")
step$anova # display results

Alternativ kannst du eine All-Subset-Regression mit der Funktion leaps( ) aus dem Paket leaps durchführen. Im folgenden Code gibt nbest die Anzahl der zu meldenden Teilmengen jeder Größe an. Hier werden die zehn besten Modelle für jede Untergruppengröße (1 Prädiktor, 2 Prädiktoren usw.) angegeben.

# All Subsets Regression
library(leaps)
attach(mydata)
leaps<-regsubsets(y~x1+x2+x3+x4,data=mydata,nbest=10)
# view results
summary(leaps)
# plot a table of models showing variables in each model.
#
models are ordered by the selection statistic.
plot(leaps,scale="r2")
# plot statistic by subset size
library(car)
subsets(leaps, statistic="rsq")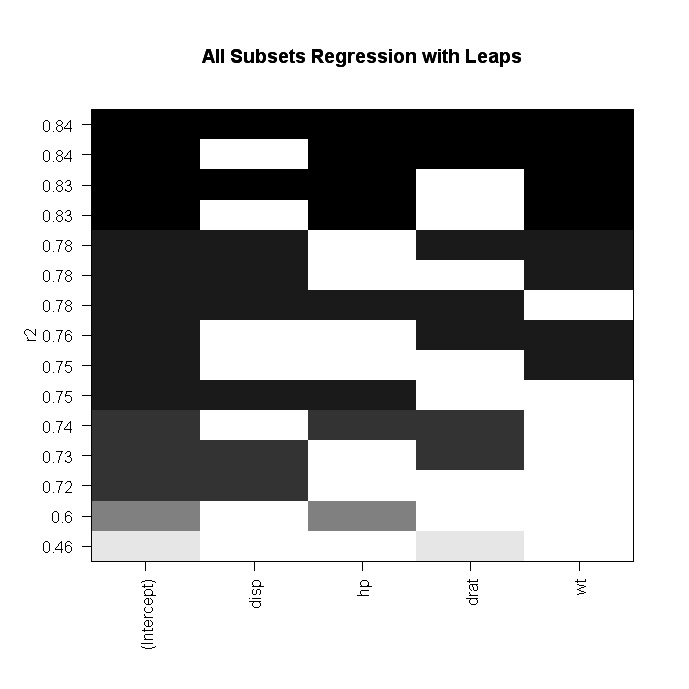

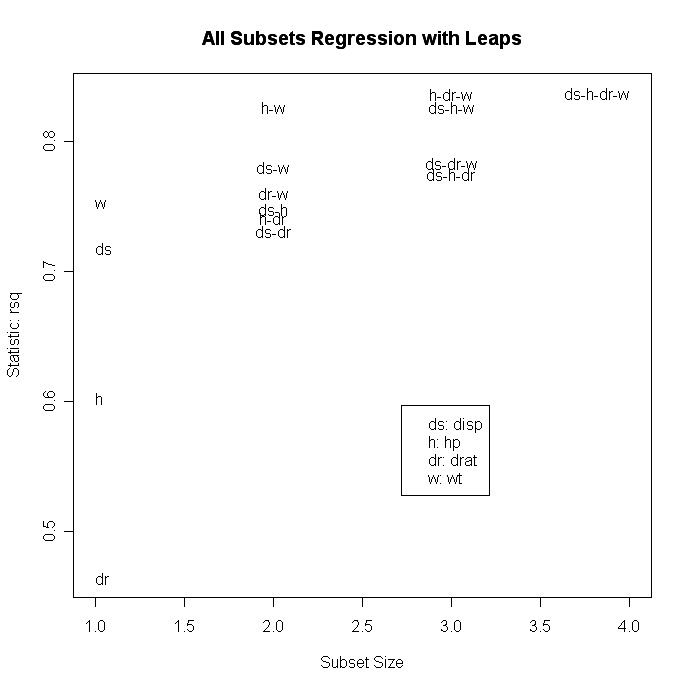
Andere Optionen für plot( ) sind bic, Cp und adjr2. Weitere Optionen für das Plotten mitsubset( ) sind bic, cp, adjr2 und rss.

Relative Wichtigkeit

Das Paket relaimpo</a > liefert Maße für die relative Bedeutung der einzelnen Prädiktoren im Modell. Siehe help(calc.relimp) für Details zu den vier zur Verfügung gestellten Maßen der relativen Wichtigkeit.

# Calculate Relative Importance for Each Predictor
library(relaimpo)
calc.relimp(fit,type=c("lmg","last","first","pratt"),
   rela=TRUE)

# Bootstrap Measures of Relative Importance (1000 samples)
boot <- boot.relimp(fit, b = 1000, type = c("lmg",
  "last", "first", "pratt"), rank = TRUE,
  diff = TRUE, rela = TRUE)
booteval.relimp(boot) # print result
plot(booteval.relimp(boot,sort=TRUE)) # plot result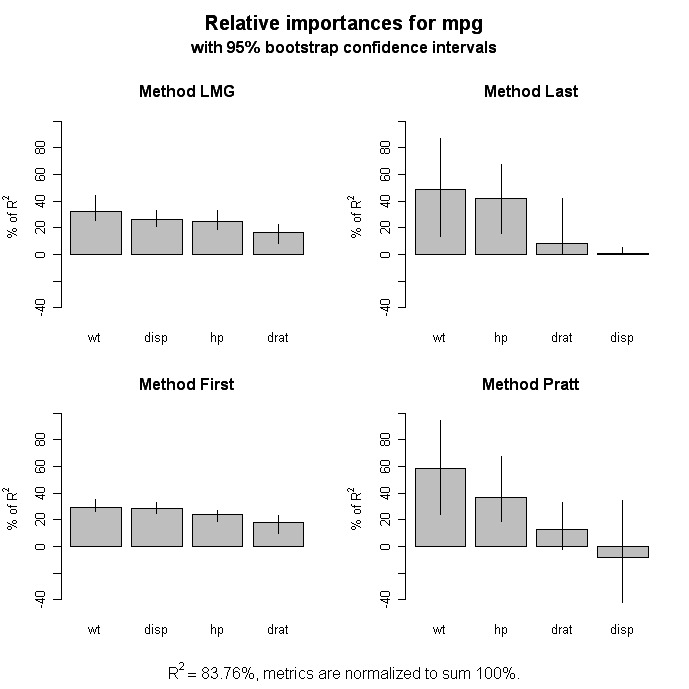

Grafische Erweiterungen

Das Autopaket bietet eine Vielzahl von Plots für die Regression, einschließlich Plots für hinzugefügte Variablen und erweiterte Diagnose- und Scatterplots.

Weiter gehen

Nichtlineare Regression

Das nls-Paket bietet Funktionen für die nichtlineare Regression. In John Fox' Nonlinear Regression and Nonlinear Least Squares</a > findest du einen Überblick. Huet und Kollegen Statistische Werkzeuge für nichtlineare Regression: A Practical Guide with S-PLUS and R Examples</a > ist ein wertvolles Nachschlagewerk.

Robuste Regression

In R gibt es viele Funktionen, die bei der robusten Regression helfen. Du kannst zum Beispiel eine robuste Regression mit der Funktion rlm( ) aus dem MASS-Paket durchführen. John Fox's (wer sonst?) Robuste Regression</a > bietet einen guten Überblick für den Anfang. Auf der Website der UCLA Statistical Computing findest du Beispiele für robuste Regression</a > .

Das Robust-Paket bietet eine umfassende Bibliothek mit robusten Methoden, einschließlich Regression. Das Paket robustbase</a > bietet auch grundlegende robuste Statistiken einschließlich Modellauswahlmethoden. Und David Olive hat eine ausführliche Online-Rezension von Angewandte robuste Statistik</a> mit R-Beispielcode bereitgestellt.

Zum Üben

Dieser Kurs über maschinelles Lernen in R</a> beinhaltet Übungen zur multiplen Regression und Kreuzvalidierung .