Regresión lineal en Python: Tu guía para la modelización predictiva

Python, con su rico ecosistema de bibliotecas como NumPy, statsmodels y scikit-learn, se ha convertido en el lenguaje de referencia para los científicos de datos. Su facilidad de uso y versatilidad lo hacen perfecto tanto para comprender los fundamentos teóricos de la regresión lineal como para aplicarla en situaciones reales.

En esta guía, te guiaré a través de todo lo que necesitas saber sobre la regresión lineal en Python. Empezaremos definiendo qué es la regresión lineal y por qué es tan importante. A continuación, nos adentraremos en la mecánica, explorando las ecuaciones y supuestos subyacentes. Aprenderás a realizar regresiones lineales utilizando varias bibliotecas de Python, desde cálculos manuales con NumPy hasta implementaciones racionalizadas con scikit-learn. Cubriremos tanto la regresión lineal simple como la múltiple, y te mostraré cómo evaluar tus modelos y mejorar su rendimiento.

¿Qué es la regresión lineal?

La regresión lineal es un método estadístico utilizado para modelizar la relación entre una variable dependiente (objetivo) y una o más variables independientes (predictores). El objetivo es encontrar una ecuación lineal que describa mejor esta relación.

La regresión lineal se utiliza ampliamente para el modelado predictivo, la estadística inferencial y la comprensión de las relaciones en los datos. Sus aplicaciones incluyen la previsión de ventas, la evaluación del riesgo y el análisis del impacto de distintas variables en un resultado objetivo.

¿Qué es la regresión lineal simple?

Para la regresión lineal simple, adoptaría la forma de una línea en el espacio bidimensional; para la regresión lineal múltiple (con dos variables independientes), la relación se representa mediante un plano en el espacio tridimensional; Para un número aún mayor de variables independientes, la ecuación describe un hiperplano en un espacio de dimensiones superiores.

Empecemos con un modelo de regresión lineal simple, que, como ya he dicho, sólo tiene una variable predictora. Se representa mediante esta ecuación:

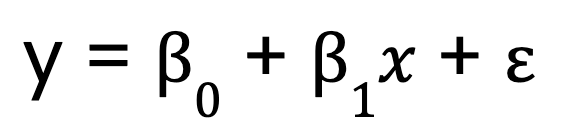
Dónde:

• y es la variable dependiente,
• x es la variable independiente,
• _B0 es el intercepto,
• _B1 es el coeficiente (pendiente) de la variable independiente,
• representa el término de error.

¿Qué es la regresión lineal múltiple?

En cambio, la regresión lineal múltiple amplía este concepto para incluir múltiples variables predictoras:

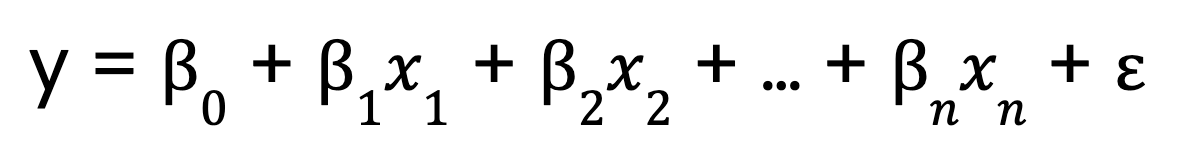
Dónde:

• 0 es el intercepto,
• x₁, x₂, ..., x_n son las variables predictoras
• 1,2, ..., n son los coeficientes correspondientes a cada variable predictora,
• es el término de error.

La mecánica de la regresión lineal

Para entender cómo funciona la regresión lineal, vamos a desglosar sus componentes clave.

La ecuación del modelo lineal

Anteriormente vimos ecuaciones de regresión lineal, tanto con un único predictor como con varios. Pero ahora, permíteme hablar de un aspecto importante de las ecuaciones. 

El término lineal en regresión lineal se refiere a la forma funcional del modelo, no necesariamente a la forma de los datos. Concretamente, significa que

1. El modelo es lineal en sus parámetros. Esto significa que cada predictor se multiplica por un coeficiente y se suma.
2. La relación entre la variable dependiente y los predictores es aditivalo que significa que los cambios en cada predictor tienen un efecto consistente en la variable dependiente.
3. No se aplica exponenciación, multiplicación entre variables ni transformaciones no lineales a los parámetros.

Método de mínimos cuadrados ordinarios (MCO)

Para determinar la línea que mejor se ajusta, la regresión lineal utiliza el método de los mínimos cuadrados ordinarios (MCO) (MCO). OLS minimiza la suma de errores al cuadrado:

OLS minimiza la suma de errores al cuadrado:

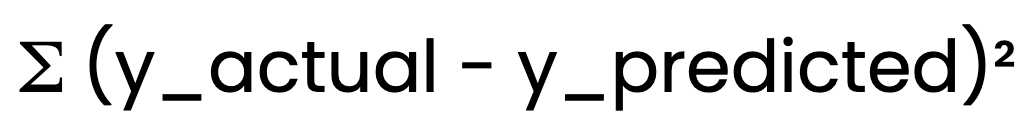
Esto garantiza que el modelo proporcione las mejores estimaciones posibles de B₀ y B₁.

Supuestos de la regresión lineal

Para que la regresión lineal produzca resultados fiables, deben cumplirse ciertos supuestos:

1. Linealidad: La relación entre la variable independiente y la dependiente debe ser lineal.
2. Independencia de los errores: Los residuos (errores) no deben estar correlacionados entre sí.
3. Varianza constante (homocedasticidad): La dispersión de los residuos debe permanecer constante en todos los valores.
4. Normalidad de los residuos: Los residuos deben seguir una distribución normal.

La validación de estos supuestos garantiza que nuestro modelo sea fiable y válido. Por ejemplo, si la relación entre las variables no es lineal, las predicciones del modelo pueden ser inexactas. Si hay heteroscedasticidad, los intervalos de confianza podrían ser erróneos.

Formas de hacer regresión lineal en Python

La regresión lineal puede implementarse en Python utilizando distintos enfoques. Te guiaré a través de tres métodos comunes: cálculos manuales con NumPy, modelado estadístico detallado con statsmodels y aprendizaje automático racionalizado con scikit-learn.

Método de cálculo manual (NumPy)

Para una regresión lineal simple (una variable predictora), puedes calcular manualmente los parámetros de la regresión utilizando NumPy. Esto implica primero calcular la media de las variables independiente y dependiente. A continuación, calculamos la pendiente (_B0):

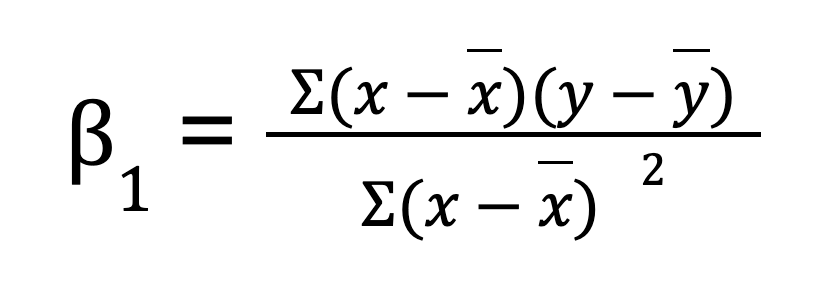
Una vez que tenemos la pendiente, podemos determinar el intercepto (_B1):

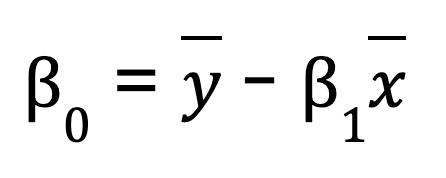
import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Compute means
x_mean = np.mean(x)
y_mean = np.mean(y)

# Compute slope (B1)
B1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean) ** 2)

# Compute intercept (B0)
B0 = y_mean - B1 * x_mean

print(f"Slope (B1): {B1}")
print(f"Intercept (B0): {B0}")

# Predicting values
y_pred = B0 + B1 * x
print("Predicted values:", y_pred)

Si te interesa simplificar el proceso, NumPy también proporciona una función incorporada np.polyfit(), que puede realizar la regresión lineal por ti con sólo una línea de código.

# Example of NumPy's polyfit
np.polyfit(x, y, 1)  # 1 stands for the degree of the polynomial (linear)

Aunque este método es útil para comprender las matemáticas que hay detrás de la regresión lineal simple, es poco práctico para grandes conjuntos de datos, tiene menos precisión numérica y no funciona para problemas de regresión múltiple.

Utilizar una biblioteca estadística (statsmodels)

Una forma más eficaz de realizar la regresión lineal es utilizar statsmodelsuna biblioteca que proporciona modelos estadísticos y herramientas de análisis.

Pasos para ajustar un mínimos cuadrados ordinarios (MCO) con Statsmodels:

1. Prepara los datos: Asegúrate de que la variable independiente está estructurada correctamente.

2. Añade una constante: Esto tiene en cuenta el término de intercepción de la ecuación.

3. Adapta el modelo: Utiliza OLS() de statsmodels para estimar los parámetros de regresión.

4. Analiza los resultados: La función .summary() proporciona información detallada del modelo, incluidos los coeficientes, los valores p y los valores R-cuadrado.

import numpy as np
import statsmodels.api as sm

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Add constant for intercept term
X = sm.add_constant(x)

# Fit OLS model
model = sm.OLS(y, X).fit()

# Print summary
print(model.summary())

Utilizar una biblioteca de aprendizaje automático (Scikit-Learn)

scikit-learn se utiliza mucho por su sencillez, escalabilidad e integración con otras herramientas de aprendizaje automático. En se ofrece una forma sencilla y eficaz de realizar una regresión lineal utilizando la clase LinearRegression.

1. Importa la biblioteca y carga tu conjunto de datos.

2. Modifica la variable predictora si es necesario (para la regresión de una sola variable).

3. Crear una instancia del modelo utilizando LinearRegression().

4. Ajusta el modelo a los datos de entrenamiento.

5. Recupera los parámetros del modelo: El atributo .coeff_ devuelve la pendiente, mientras que .intercept_ proporciona la intercepción.

import numpy as np
from sklearn.linear_model import LinearRegression

# Sample data
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)  # Reshape for scikit-learn
y = np.array([2, 4, 5, 4, 5])

# Create model instance
model = LinearRegression()

# Fit the model
model.fit(x, y)

# Get model parameters
print(f"Slope (B1): {model.coef_[0]}")
print(f"Intercept (B0): {model.intercept_}")

# Predict values
y_pred = model.predict(x)
print("Predicted values:", y_pred)

Otros métodos importantes

Además de NumPy, statsmodels y scikit-learn, otras bibliotecas de Python ofrecen funciones de regresión:

• Pandas: Útil para el análisis exploratorio de datos y el modelado rápido de tendencias.
• SciPy: Incluye funciones estadísticas que pueden utilizarse para el análisis de regresión.
• TensorFlow y PyTorch: Aunque son principalmente para el aprendizaje profundo, pueden manejar eficazmente tareas de regresión lineal.

Cada enfoque tiene sus ventajas en función de la complejidad de tu tarea de regresión y del nivel de análisis necesario.

Regresión lineal en Python con uno o más predictores

La regresión lineal puede manejar relaciones simples y complejas. En esta sección, exploraremos cómo implementar la regresión lineal con un predictor (simple) y múltiples predictores (múltiple) utilizando Python.

Regresión lineal simple en Python

Para una regresión lineal simple en Python, seguimos estos pasos:

Paso 1: Calcula la correlación

El coeficiente de correlación mide la fuerza de la relación entre x y y. Lo encontramos utilizando NumPy:

import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])  # Independent variable
y = np.array([2, 4, 5, 4, 5])  # Dependent variable

correlation = np.corrcoef(x, y)[0, 1]
print("Correlation:", correlation)

Paso 2: Calcula la pendiente y el intercepto

La pendiente_B1 se calcula como

beta_1 = correlation * (np.std(y) / np.std(x))

Quizá notes que esta ecuación es ligeramente diferente de la anterior, en la que hallé la pendiente sumando los productos de las desviaciones entre $x$ y yy dividiendo por la suma de las desviaciones al cuadrado en $x$. Este nuevo método, que utiliza la correlación y la desviación típica, puede parecer diferente, pero en realidad es lo mismo.

El coeficiente de correlación $r$ se calcula como la suma de los productos de las diferencias respecto a la media, dividida por la raíz cuadrada del producto de la suma de las diferencias al cuadrado en $x$ y $y$. Reescribiendo la ecuación anterior, podemos expresar la pendiente como $r$ multiplicada por la relación de las desviaciones típicas de $y$ y $x$haciendo que las dos formas sean equivalentes desde el punto de vista algebraico.

Ahora, la interceptación:

beta_0 = np.mean(y) - beta_1 * np.mean(x)

Paso 3: Haz predicciones utilizando los parámetros calculados

Ahora que tenemos los coeficientes, podemos hallar los valores predichos.

y_pred = beta_0 + beta_1 * x

Creo que seguir estos pasos es útil para comprender los cálculos subyacentes antes de utilizar bibliotecas como scikit-learn.

Regresión lineal múltiple en Python

La regresión lineal múltiple amplía el concepto de regresión lineal simple para modelizar las relaciones entre una variable dependiente y múltiples variables independientes. Esto nos permite analizar conjuntos de datos más complejos en los que un solo predictor no explica suficientemente la variación de la variable dependiente.

Para realizar una regresión lineal múltiple en Python, solemos utilizar el álgebra matricial para calcular los coeficientes que minimizan la suma de cuadrados residual. Una fórmula comúnmente enseñada para calcular los coeficientes en la regresión lineal múltiple se conoce como ecuación normal:

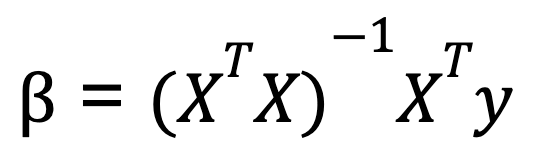
Dónde:

• X es la matriz de variables independientes (con una columna de unos para el intercepto),
• y es el vector de valores de la variable dependiente.
• X^T es la transposición de la matriz de X.
• (X^TX)^-1 es la inversa de X^TX.

Esta ecuación da los valores óptimos de los coeficientes que minimizan la suma de errores al cuadrado.

Aquí tienes un ejemplo de cómo realizar una regresión lineal múltiple con Python, utilizando NumPy para las operaciones matriciales:

import numpy as np

# Sample data: two predictors and one dependent variable
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add a column of ones to include the intercept in the model
X = np.column_stack((np.ones(X.shape[0]), X))

# Calculate beta coefficients using the normal equation
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print("Coefficients:", beta)

Este método funciona bien cuando los predictores son independientes, pero si los predictores están muy correlacionados, la inversión de la matriz se vuelve inestable. Por esta razón, bibliotecas como scikit-learn utilizan un método numéricamente más estable basado en la descomposición QR para calcular los coeficientes de regresión. Así que, aunque podamos calcular los coeficientes utilizando la ecuación normal, debes saber que cuando utilizamos la función LinearRegression() de scikitlearn, la descomposición qr está funcionando bajo el capó.

Abordar la multicolinealidad

Ahora es un buen momento para mencionar una cosa que aparece como preocupación en la regresión lineal múltiple en Python. La multicolinealidad se produce cuando dos o más variables independientes están muy correlacionadas, lo que dificulta aislar sus efectos individuales. Esto puede dar lugar a estimaciones inestables de los coeficientes. Para detectar y mitigar la multicolinealidad, puedes calcular el factor de inflación de la varianza (VIF). También puedes eliminar las variables muy correlacionadas, o bien utilizar técnicas de regularización como la regresión ridge y la regresión lasso.

Diagnóstico y evaluación de modelos de regresión lineal en Python

Tras construir tu modelo de regresión lineal, el siguiente paso es evaluar su rendimiento y validar que cumple los supuestos subyacentes. Esto garantiza la fiabilidad de tus predicciones y te ayuda a identificar posibles mejoras.

Análisis residual

El análisis de residuos es una parte fundamental de los diagnósticos de regresión lineal. Ayuda a comprobar los supuestos de la regresión lineal e identificar cualquier infracción. Los residuos deben estar dispersos aleatoriamente en torno a cero, sin un patrón discernible. Aquí es donde entran en juego herramientas visuales como los gráficos residuales y los gráficos Q-Q:

1. Parcela residual: Un gráfico de dispersión de los residuos frente a los valores predichos (o variables independientes) ayuda a comprobar si hay alguna relación que el modelo no haya tenido en cuenta. Lo ideal es que el gráfico muestre una dispersión aleatoria sin un patrón claro, lo que sugiere que el modelo ha captado bien la relación lineal.
2. Gráfico Q-Q (Gráfico Cuantil-Cuantil): Un gráfico Q-Q ayuda a evaluar si los residuos siguen una distribución normal. Para que la regresión lineal sea válida, los residuos deben tener una distribución aproximadamente normal. Una línea recta en el gráfico Q-Q indica normalidad.

En Python, podemos crear estos gráficos fácilmente con bibliotecas como matplotlib, seaborn, y statsmodels.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# Sample data and linear regression model
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add an intercept term
X = sm.add_constant(X)

# Fit the linear regression model
model = sm.OLS(y, X).fit()

# Get the residuals
residuals = model.resid

# 1. Residual Plot
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')

# 2. Q-Q Plot
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line ='45', ax=plt.gca())
plt.title('Q-Q Plot')

plt.tight_layout()
plt.show()

Métricas de evaluación

Aparte del análisis visual, las métricas cuantitativas son esenciales para evaluar lo bien que se ajusta a los datos el modelo de regresión lineal. Algunas métricas clave de evaluación son

1. R-cuadrado (R²): Esta métrica te indica qué parte de la varianza de la variable dependiente puede explicarse por las variables independientes. Un valor de R² cercano a 1 indica que el modelo explica una gran proporción de la varianza, mientras que un valor cercano a 0 significa que el modelo no se ajusta bien a los datos.
2. R-cuadrado ajustado: Esta métrica ajusta R² al número de predictores del modelo. Es útil para comparar modelos con distintos números de predictores.
3. Error cuadrático medio (RMSE): El RMSE mide la magnitud media de los errores en las predicciones del modelo, con las mismas unidades que la variable dependiente. Un RMSE más bajo indica un mejor rendimiento predictivo.
4. Error medio absoluto (MAE): El MAE mide la magnitud media de los errores en las predicciones del modelo, pero a diferencia del RMSE, no penaliza tanto los errores grandes. Es más fácil de interpretar, ya que está en las mismas unidades que la variable dependiente.

Estas métricas pueden calcularse fácilmente en Python utilizando statsmodels o scikit-learn:

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

# Make predictions using the model
y_pred = model.predict(X)

# R-squared
r_squared = r2_score(y, y_pred)
print("R-squared:", r_squared)

# Adjusted R-squared (calculated manually)
n = len(y)  # number of data points
p = X.shape[1] - 1  # number of predictors (excluding intercept)
adj_r_squared = 1 - (1 - r_squared) * (n - 1) / (n - p - 1)
print("Adjusted R-squared:", adj_r_squared)

# RMSE
rmse = np.sqrt(mean_squared_error(y, y_pred))
print("Root Mean Squared Error (RMSE):", rmse)

# MAE
mae = mean_absolute_error(y, y_pred)
print("Mean Absolute Error (MAE):", mae)

Al evaluar estas métricas, obtienes información sobre la precisión del modelo, la bondad del ajuste y lo bien que el modelo se generaliza a nuevos datos.

Mejorar tu modelo de regresión

Una vez que hayas evaluado tu modelo de regresión lineal, el siguiente paso es explorar formas de mejorar su rendimiento. Un enfoque habitual es a través de transformaciones de rasgos, que pueden abordar las relaciones no lineales y ayudar al modelo a captar mejor los patrones subyacentes en los datos.

Transformaciones de rasgos

Recuerda que, en la regresión lineal, el modelo supone una relación lineal entre las variables independientes (predictores) y la variable dependiente. Sin embargo, muchos conjuntos de datos del mundo real tienen relaciones no lineales que un simple modelo lineal puede no captar bien. Aplicando transformaciones de rasgos, como transformaciones logarítmicas o de raíz cuadrada, a veces puedes mejorar el rendimiento del modelo.

Transformación logarítmica

Suele utilizarse cuando un rasgo presenta un crecimiento exponencial o tiene grandes valores positivos. Por ejemplo, transformar datos de ingresos muy sesgados (en los que dominan unos pocos valores de ingresos muy altos) puede hacer que la distribución sea más normal.

import numpy as np
df['log_income'] = np.log(df['income'] + 1)  # +1 to avoid log(0)

Transformación de raíz cuadrada

Esto es útil para rasgos que siguen una relación cuadrática. Por ejemplo, una característica que represente recuentos (como el número de visitas a un sitio web) puede beneficiarse de una transformación de raíz cuadrada.

df['sqrt_visits'] = np.sqrt(df['visits'])

Al transformar estas características, estás ayudando al modelo a captar mejor las relaciones que antes no captaba el enfoque lineal. La clave está en probar diferentes transformaciones y observar el efecto en el rendimiento del modelo. No es un planteamiento único, y requiere pruebas empíricas.

Normalización y estandarización

Además de las transformaciones de características, también es importante comprender el impacto de la normalización y la estandarización en tu modelo de regresión, especialmente cuando tratas con características que tienen diferentes unidades o escalas. La normalización reescala los valores de las características a un intervalo, normalmente [0, 1]. La estandarización reescala las características para que tengan una media de 0 y una desviación típica de 1.

Cuando tienes múltiples predictores, normalizar o estandarizar los datos ayuda a interpretar los coeficientes de forma más significativa. Es decir, t ayuda a mostrar cuánto contribuye cada variable predictora a la variable dependiente en relación con otros predictores. Esto es especialmente útil cuando los predictores están en escalas diferentes.

Conclusión

Desarrollar una sólida comprensión de la regresión lineal requiere práctica y exploración continuas. Para profundizar en tus conocimientos, considera la posibilidad de aprender más sobre el tratamiento de la multicolinealidad, la heteroscedasticidad y las técnicas de regularización como la regresión Ridge y Lasso. Reforzar tus conocimientos sobre la descomposición QR y el factor de inflación de la varianza también puede mejorar el diagnóstico de los modelos. Además, entender la normalización frente a la estandarización puede mejorar las decisiones de escalado de características.