Lineare Regression in Python: Dein Leitfaden für prädiktive Modellierung

Python mit seinem reichhaltigen Ökosystem an Bibliotheken wie NumPy, statsmodels und scikit-learn ist zur bevorzugten Sprache für Datenwissenschaftler geworden. Seine Benutzerfreundlichkeit und Vielseitigkeit machen es perfekt, um sowohl die theoretischen Grundlagen der linearen Regression zu verstehen als auch sie in realen Szenarien umzusetzen.

In diesem Leitfaden erkläre ich dir alles, was du über lineare Regression in Python wissen musst. Wir beginnen damit, zu definieren, was lineare Regression ist und warum sie so wichtig ist. Dann schauen wir uns die Mechanik an und erforschen die zugrunde liegenden Gleichungen und Annahmen. Du lernst, wie du mit verschiedenen Python-Bibliotheken lineare Regressionen durchführen kannst, von manuellen Berechnungen mit NumPy bis hin zu optimierten Implementierungen mit scikit-learn. Wir werden sowohl die einfache als auch die multiple lineare Regression behandeln, und ich zeige dir, wie du deine Modelle auswerten und ihre Leistung verbessern kannst.

Was ist lineare Regression?

Die lineare Regression ist eine statistische Methode zur Modellierung der Beziehung zwischen einer abhängigen Variable (Ziel) und einer oder mehreren unabhängigen Variablen (Prädiktoren). Das Ziel ist es, eine lineare Gleichung zu finden, die diese Beziehung am besten beschreibt.

Die lineare Regression wird häufig für Vorhersagemodelle, Schlussfolgerungsstatistiken und das Verständnis von Beziehungen in Daten verwendet. Zu den Anwendungsbereichen gehören Umsatzprognosen, Risikobewertungen und die Analyse der Auswirkungen verschiedener Variablen auf ein Zielergebnis.

Was ist eine einfache lineare Regression?

Bei einer einfachen linearen Regression würde dies die Form einer Linie im zweidimensionalen Raum annehmen; bei einer multiplen linearen Regression (mit zwei unabhängigen Variablen) wird die Beziehung durch eine Ebene im dreidimensionalen Raum dargestellt; bei noch mehr unabhängigen Variablen beschreibt die Gleichung eine Hyperebene im höherdimensionalen Raum.

Beginnen wir mit einem einfachen linearen Regressionsmodell, das, wie bereits erwähnt, nur eine Vorhersagevariable hat. Sie wird durch diese Gleichung dargestellt:

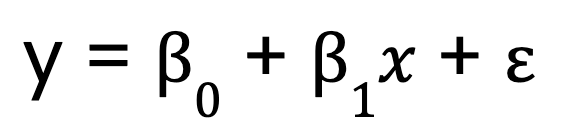
Wo:

• y ist die abhängige Variable,
• x ist die unabhängige Variable,
• _B0 ist der Schnittpunkt,
• _B1 ist der Koeffizient (Steigung) der unabhängigen Variable,
• steht für den Fehlerterm.

Was ist eine multiple lineare Regression?

Im Gegensatz dazu erweitert die multiple lineare Regression dieses Konzept um mehrere Vorhersagevariablen:

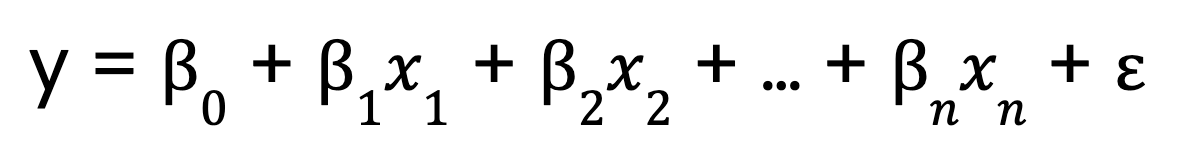
Wo:

• 0 ist der Schnittpunkt,
• x₁, x₂, ..., x_n sind die Prädiktorvariablen
• 1,2, ..., n sind die Koeffizienten für die einzelnen Prädiktoren,
• ist der Fehlerterm.

Die Mechanik hinter der linearen Regression

Um zu verstehen, wie die lineare Regression funktioniert, müssen wir ihre wichtigsten Bestandteile aufschlüsseln.

Die lineare Modellgleichung

Wir haben oben Gleichungen für die lineare Regression gesehen, sowohl mit einem einzelnen als auch mit mehreren Prädiktoren. Aber jetzt möchte ich über einen wichtigen Aspekt der Gleichungen sprechen. 

Der Begriff linear in der linearen Regression bezieht sich auf die funktionale Form des Modells, nicht unbedingt auf die Form der Daten. Konkret bedeutet das, dass:

1. Das Modell ist linear in seinen Parametern. Das heißt, jeder Prädiktor wird mit einem Koeffizienten multipliziert und summiert.
2. Die Beziehung zwischen der abhängigen Variable und den Prädiktoren ist additivDas bedeutet, dass Veränderungen bei jedem Prädiktor eine gleichbleibende Wirkung auf die abhängige Variable haben.
3. Es werden keine Potenzierung, Multiplikation zwischen Variablen oder nichtlineare Transformationen werden auf die Parameter angewendet.

Methode der gewöhnlichen kleinsten Quadrate (OLS)

Die lineare Regression verwendet zur Bestimmung der am besten passenden Linie die gewöhnlichen kleinsten Quadrate (OLS) Methode. OLS minimiert die Summe der quadratischen Fehler:

OLS minimiert die Summe der quadratischen Fehler:

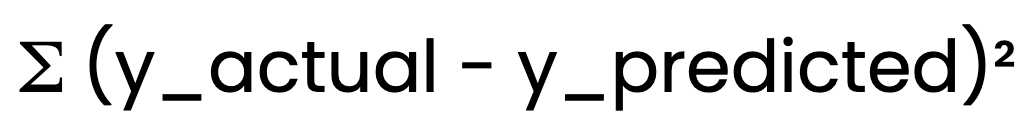
So wird sichergestellt, dass das Modell die bestmöglichen Schätzungen für B₀ und B₁.

Annahmen der linearen Regression

Damit eine lineare Regression zuverlässige Ergebnisse liefert, müssen bestimmte Annahmen erfüllt sein:

1. Linearität: Die Beziehung zwischen der unabhängigen und der abhängigen Variable sollte linear sein.
2. Unabhängigkeit von Fehlern: Die Residuen (Fehler) sollten nicht miteinander korreliert sein.
3. Konstante Varianz (Homoskedastizität): Die Streuung der Residuen sollte über alle Werte hinweg konstant bleiben.
4. Normalität der Residuen: Die Residuen sollten einer Normalverteilung folgen.

Die Überprüfung dieser Annahmen stellt sicher, dass unser Modell sowohl zuverlässig als auch gültig ist. Wenn zum Beispiel die Beziehung zwischen den Variablen nicht linear ist, können die Vorhersagen des Modells ungenau sein. Wenn es Heteroskedastizität gibt, könnten die Konfidenzintervalle falsch sein.

Wie man eine lineare Regression in Python durchführt

Die lineare Regression kann in Python mit verschiedenen Ansätzen umgesetzt werden. Ich führe dich durch drei gängige Methoden: manuelle Berechnungen mit NumPy, detaillierte statistische Modellierung mit statsmodels und rationalisiertes maschinelles Lernen mit scikit-learn.

Manueller Berechnungsansatz (NumPy)

Für eine einfache lineare Regression (eine Vorhersagevariable) kannst du die Regressionsparameter manuell mit NumPyberechnen . Dazu wird zunächst der Mittelwert der unabhängigen und abhängigen Variablen berechnet. Dann berechnen wir die Steigung (_B0):

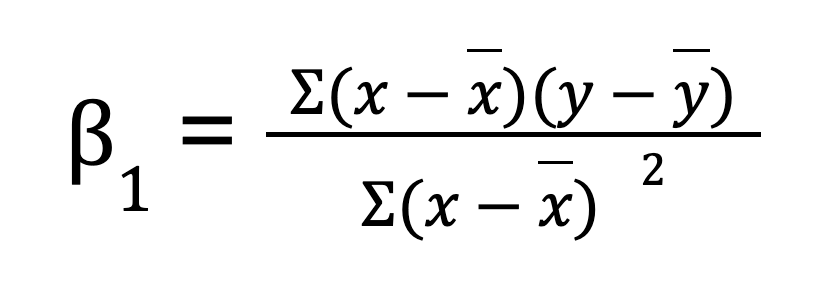
Sobald wir die Steigung haben, können wir den Achsenabschnitt (_B1) bestimmen:

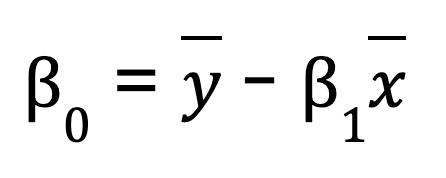
import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Compute means
x_mean = np.mean(x)
y_mean = np.mean(y)

# Compute slope (B1)
B1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean) ** 2)

# Compute intercept (B0)
B0 = y_mean - B1 * x_mean

print(f"Slope (B1): {B1}")
print(f"Intercept (B0): {B0}")

# Predicting values
y_pred = B0 + B1 * x
print("Predicted values:", y_pred)

Wenn du den Prozess vereinfachen möchtest, bietet NumPy auch eine eingebaute Funktion np.polyfit(), mit der du eine lineare Regression mit nur einer Zeile Code durchführen kannst.

# Example of NumPy's polyfit
np.polyfit(x, y, 1)  # 1 stands for the degree of the polynomial (linear)

Diese Methode ist zwar nützlich, um die Mathematik hinter einer einfachen linearen Regression zu verstehen, aber sie ist unpraktisch für große Datensätze, hat eine geringere numerische Genauigkeit und funktioniert nicht bei Problemen mit multiplen Regressionen.

Verwendung einer statistischen Bibliothek (statsmodels)

Eine effizientere Methode zur Durchführung einer linearen Regression ist die Verwendung von statsmodelseine Bibliothek, die statistische Modelle und Analysewerkzeuge bereitstellt.

Schritte zur Anpassung einer Gewöhnliche kleinste Quadrate (OLS) Modells mit Statsmodels:

1. Bereite die Datenvor: Achte darauf, dass die unabhängige Variable richtig strukturiert ist.

2. Füge eine Konstantehinzu: Dadurch wird der Intercept-Term in der Gleichung berücksichtigt.

3. Passe das Modellan: Nutze OLS() von statsmodels, um die Regressionsparameter zu schätzen.

4. Analysiere die Ergebnisse: Die Funktion .summary() bietet detaillierte Einblicke in das Modell, einschließlich Koeffizienten, p-Werte und R-Quadrat-Werte.

import numpy as np
import statsmodels.api as sm

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Add constant for intercept term
X = sm.add_constant(x)

# Fit OLS model
model = sm.OLS(y, X).fit()

# Print summary
print(model.summary())

Verwendung einer Bibliothek für maschinelles Lernen (scikit-learn)

scikit-learn wird wegen seiner Einfachheit, Skalierbarkeit und Integration mit anderen Machine-Learning-Tools häufig verwendet. Es bietet eine einfache und effiziente Möglichkeit, eine lineare Regression mit der Klasse LinearRegression durchzuführen.

1. Importiere die Bibliothek und lade deinen Datensatz.

2. Verändere die Prädiktorvariable wenn nötig (bei Regression mit einer einzigen Variable).

3. Erstelle eine Modellinstanz mit LinearRegression().

4. Passe das Modell an die Trainingsdaten an.

5. Rufe die Modellparameterab: Das Attribut .coeff_ liefert die Steigung, während .intercept_ den Achsenabschnitt angibt.

import numpy as np
from sklearn.linear_model import LinearRegression

# Sample data
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)  # Reshape for scikit-learn
y = np.array([2, 4, 5, 4, 5])

# Create model instance
model = LinearRegression()

# Fit the model
model.fit(x, y)

# Get model parameters
print(f"Slope (B1): {model.coef_[0]}")
print(f"Intercept (B0): {model.intercept_}")

# Predict values
y_pred = model.predict(x)
print("Predicted values:", y_pred)

Andere wichtige Methoden

Neben NumPy, statsmodels und scikit-learn bieten mehrere andere Python-Bibliotheken Regressionsfunktionen:

• Pandas: Nützlich für explorative Datenanalysen und schnelle Trendmodellierung.
• SciPy: Enthält statistische Funktionen, die für die Regressionsanalyse verwendet werden können.
• TensorFlow & PyTorch: Obwohl sie in erster Linie für Deep Learning gedacht sind, können sie auch Aufgaben der linearen Regression effektiv lösen.

Jeder Ansatz hat seine Vorteile. Das hängt von der Komplexität deiner Regressionsaufgabe ab.

Lineare Regression in Python mit einem oder mehreren Prädiktoren

Die lineare Regression kann sowohl einfache als auch komplexe Zusammenhänge erfassen. In diesem Abschnitt erfahren wir, wie du mit Python eine lineare Regression mit einem Prädiktor (einfach) und mehreren Prädiktoren (mehrfach) durchführen kannst.

Einfache lineare Regression in Python

Für eine einfache lineare Regression in Python gehen wir folgendermaßen vor:

Schritt 1: Berechne die Korrelation

Der Korrelationskoeffizient misst die Stärke der Beziehung zwischen x und y. Wir finden sie mit NumPy:

import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])  # Independent variable
y = np.array([2, 4, 5, 4, 5])  # Dependent variable

correlation = np.corrcoef(x, y)[0, 1]
print("Correlation:", correlation)

Schritt 2: Berechne die Steigung und den Achsenabschnitt

Die Steigung_B1 wird berechnet als:

beta_1 = correlation * (np.std(y) / np.std(x))

Du wirst feststellen, dass diese Gleichung etwas anders aussieht als die vorherige, bei der ich die Steigung durch Summierung der Produkte der Abweichungen zwischen $x$ und yund dann durch die Summe der quadrierten Abweichungen in $x$. Diese neue Methode, bei der Korrelation und Standardabweichung verwendet werden, mag anders aussehen, ist aber eigentlich die gleiche. Wenn wir die vorherige Gleichung umschreiben, können wir die Steigung wie folgt ausdrücken $r$ multipliziert mit dem Verhältnis der Standardabweichungen von $y$ und $x$Damit sind die beiden Formen algebraisch gleichwertig.

Und nun zum Abfangen:

beta_0 = np.mean(y) - beta_1 * np.mean(x)

Schritt 3: Mache Vorhersagen anhand der berechneten Parameter

Da wir nun die Koeffizienten haben, können wir die vorhergesagten Werte ermitteln.

y_pred = beta_0 + beta_1 * x

Ich denke, es ist hilfreich, diese Schritte durchzugehen, um die zugrunde liegenden Berechnungen zu verstehen, bevor du Bibliotheken wie scikit-learn verwendest.

Multiple lineare Regression in Python

Die multiple lineare Regression erweitert das Konzept der einfachen linearen Regression, um Beziehungen zwischen einer abhängigen Variable und mehreren unabhängigen Variablen zu modellieren. So können wir komplexere Datensätze analysieren, bei denen ein Prädiktor allein die Variation der abhängigen Variable nicht ausreichend erklärt.

Um eine multiple lineare Regression in Python durchzuführen, verwenden wir in der Regel Matrixalgebra, um die Koeffizienten zu berechnen, die die Summe der Restquadrate minimieren. Eine häufig gelehrte Formel zur Berechnung der Koeffizienten in der multiplen linearen Regression ist die Normalgleichung:

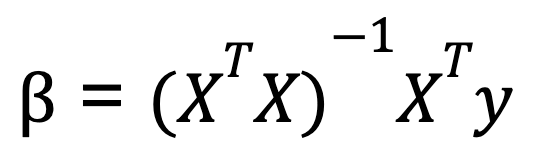
Wo:

• X ist die Matrix der unabhängigen Variablen (mit einer Spalte mit Einsen für den Intercept),
• y ist der Vektor der Werte der abhängigen Variablen.
• X^T ist die Transponierung der Matrix von X.
• (X^TX)^-1 ist die Inverse von X^TX.

Diese Gleichung gibt die optimalen Werte für die Koeffizienten an, die die Summe der quadratischen Fehler minimieren.

Hier ist ein Beispiel für die Durchführung einer multiplen linearen Regression mit Python, wobei NumPy für die Matrixoperationen verwendet wird:

import numpy as np

# Sample data: two predictors and one dependent variable
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add a column of ones to include the intercept in the model
X = np.column_stack((np.ones(X.shape[0]), X))

# Calculate beta coefficients using the normal equation
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print("Coefficients:", beta)

Diese Methode funktioniert gut, wenn die Prädiktoren unabhängig sind, aber wenn die Prädiktoren stark korreliert sind, wird die Matrixinversion instabil. Aus diesem Grund verwenden Bibliotheken wie scikit-learn eine numerisch stabilere Methode die auf der QR-Zerlegung basiert, um diegressionskoeffizienten zu berechnen. Auch wenn wir die Koeffizienten mit der normalen Gleichung berechnen können, solltest du wissen, dass bei der Verwendung der Funktion LinearRegression() von scikitlearn die qr-Zerlegung unter der Haube arbeitet.

Umgang mit Multikollinearität

Jetzt ist ein guter Zeitpunkt, um eine Sache zu erwähnen, die bei der multiplen linearen Regression in Python ein Problem darstellt. Multikollinearität liegt vor, wenn zwei oder mehr unabhängige Variablen stark miteinander korreliert sind, was es schwierig macht, ihre individuellen Auswirkungen zu isolieren. Dies kann zu instabilen Koeffizientenschätzungen führen. Um Multikollinearität zu erkennen und abzuschwächen, kannst du den Varianzinflationsfaktor (VIF) berechnen. Du kannst auch stark korrelierte Variablen entfernen oder Regularisierungstechniken wie Ridge-Regression und Lasso-Regression verwenden.

Diagnostik und Auswertung linearer Regressionsmodelle in Python

Nachdem du dein lineares Regressionsmodell erstellt hast, musst du im nächsten Schritt seine Leistung bewerten und überprüfen, ob es die zugrunde liegenden Annahmen erfüllt. Dies gewährleistet die Zuverlässigkeit deiner Vorhersagen und hilft dir, Verbesserungsmöglichkeiten zu erkennen.

Residualanalyse

Die Residualanalyse ist ein zentraler Bestandteil der linearen Regressionsdiagnostik. Sie hilft dabei, die Annahmen der linearen Regression zu überprüfen und Verstöße zu erkennen. Die Residuen sollten ohne erkennbares Muster zufällig um den Wert Null herum verstreut sein. Hier kommen visuelle Tools wie Residual Plots und Q-Q Plots ins Spiel:

1. Residual Plot: Ein Streudiagramm der Residuen gegenüber den vorhergesagten Werten (oder unabhängigen Variablen) hilft zu überprüfen, ob es einen Zusammenhang gibt, den das Modell nicht berücksichtigt hat. Im Idealfall sollte die Grafik eine zufällige Streuung ohne klares Muster zeigen, was darauf hindeutet, dass das Modell die lineare Beziehung gut erfasst hat.
2. Q-Q-Plot (Quantil-Quantil-Plot): Ein Q-Q-Diagramm hilft zu beurteilen, ob die Residuen einer Normalverteilung folgen. Damit eine lineare Regression gültig ist, sollten die Residuen ungefähr normalverteilt sein. Eine gerade Linie auf dem Q-Q-Diagramm zeigt Normalität an.

In Python können wir diese Diagramme leicht mit Bibliotheken wie matplotlib, seaborn und statsmodelserstellen.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# Sample data and linear regression model
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add an intercept term
X = sm.add_constant(X)

# Fit the linear regression model
model = sm.OLS(y, X).fit()

# Get the residuals
residuals = model.resid

# 1. Residual Plot
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')

# 2. Q-Q Plot
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line ='45', ax=plt.gca())
plt.title('Q-Q Plot')

plt.tight_layout()
plt.show()

Bewertungsmetriken

Neben der visuellen Analyse sind quantitative Messgrößen wichtig, um zu beurteilen, wie gut das lineare Regressionsmodell zu den Daten passt. Zu den wichtigsten Bewertungsmaßstäben gehören:

1. R-Quadrat (R²): Diese Kennzahl sagt dir, wie viel der Varianz in der abhängigen Variable durch die unabhängigen Variablen erklärt werden kann. Ein R²-Wert, der näher bei 1 liegt, bedeutet, dass das Modell einen großen Teil der Varianz erklärt, während ein Wert, der näher bei 0 liegt, bedeutet, dass das Modell nicht gut zu den Daten passt.
2. Bereinigtes R-Quadrat: Diese Metrik passt R² an die Anzahl der Prädiktoren im Modell an. Sie ist nützlich, um Modelle mit einer unterschiedlichen Anzahl von Prädiktoren zu vergleichen.
3. Root Mean Squared Error (RMSE): Der RMSE misst die durchschnittliche Größe der Fehler in den Vorhersagen des Modells in der gleichen Einheit wie die abhängige Variable. Ein niedriger RMSE bedeutet eine bessere Vorhersageleistung.
4. Mittlerer absoluter Fehler (MAE): MAE misst die durchschnittliche Größe der Fehler in den Vorhersagen des Modells, aber im Gegensatz zum RMSE werden große Fehler nicht so stark bestraft. Sie ist leichter zu interpretieren, da sie in denselben Einheiten wie die abhängige Variable vorliegt.

Diese Metriken können in Python mit statsmodels oder scikit-learn leicht berechnet werden:

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

# Make predictions using the model
y_pred = model.predict(X)

# R-squared
r_squared = r2_score(y, y_pred)
print("R-squared:", r_squared)

# Adjusted R-squared (calculated manually)
n = len(y)  # number of data points
p = X.shape[1] - 1  # number of predictors (excluding intercept)
adj_r_squared = 1 - (1 - r_squared) * (n - 1) / (n - p - 1)
print("Adjusted R-squared:", adj_r_squared)

# RMSE
rmse = np.sqrt(mean_squared_error(y, y_pred))
print("Root Mean Squared Error (RMSE):", rmse)

# MAE
mae = mean_absolute_error(y, y_pred)
print("Mean Absolute Error (MAE):", mae)

Durch die Auswertung dieser Metriken erhältst du Einblicke in die Genauigkeit des Modells, die Anpassungsgüte und die Generalisierbarkeit des Modells auf neue Daten.

Verbessere dein Regressionsmodell

Wenn du dein lineares Regressionsmodell ausgewertet hast, musst du im nächsten Schritt herausfinden, wie du seine Leistung verbessern kannst. Ein gängiger Ansatz sind Merkmalstransformationen, die nicht-lineare Beziehungen berücksichtigen und dem Modell helfen, die zugrunde liegenden Muster in den Daten besser zu erfassen.

Merkmalstransformationen

Denke daran, dass das Modell bei der linearen Regression eine lineare Beziehung zwischen den unabhängigen Variablen (Prädiktoren) und der abhängigen Variable annimmt. Viele reale Datensätze weisen jedoch nicht-lineare Beziehungen auf, die ein einfaches lineares Modell nicht gut erfassen kann. Durch die Anwendung von Merkmalstransformationen, wie z. B. Logarithmus- oder Quadratwurzeltransformationen, kannst du die Leistung des Modells manchmal verbessern.

Logarithmische Transformation

Dies wird oft verwendet, wenn ein Merkmal ein exponentielles Wachstum aufweist oder große positive Werte hat. Wenn du zum Beispiel stark verzerrte Einkommensdaten umwandelst (bei denen einige wenige Werte mit sehr hohem Einkommen dominieren), kann die Verteilung normaler werden.

import numpy as np
df['log_income'] = np.log(df['income'] + 1)  # +1 to avoid log(0)

Quadratwurzel-Transformation

Dies ist nützlich für Merkmale, die einer quadratischen Beziehung folgen. Zum Beispiel kann ein Merkmal, das Zählungen darstellt (wie die Anzahl der Besuche auf einer Website), von einer Quadratwurzeltransformation profitieren.

df['sqrt_visits'] = np.sqrt(df['visits'])

Indem du diese Merkmale umwandelst, hilfst du dem Modell, Zusammenhänge besser zu erfassen, die beim linearen Ansatz bisher übersehen wurden. Der Schlüssel dazu ist, verschiedene Transformationen zu testen und die Auswirkungen auf die Modellleistung zu beobachten. Es gibt keine Einheitslösung und sie erfordert empirische Tests.

Normalisierung und Standardisierung

Neben der Umwandlung von Merkmalen ist es auch wichtig, die Auswirkungen von Normalisierung und Standardisierung auf dein Regressionsmodell zu verstehen, vor allem wenn du mit Merkmalen zu tun hast, die unterschiedliche Einheiten oder Skalen haben. Die Normalisierung skaliert die Merkmalswerte auf einen Bereich, normalerweise [0, 1]. Durch die Standardisierung werden die Merkmale so skaliert, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 haben.

Wenn du mehrere Prädiktoren hast, hilft die Normalisierung oder Standardisierung der Daten dabei, die Koeffizienten sinnvoller zu interpretieren. Das heißt, t zeigt, wie viel jede Prädiktorvariable im Verhältnis zu den anderen Prädiktoren zur abhängigen Variable beiträgt. Dies ist besonders nützlich, wenn die Prädiktoren auf unterschiedlichen Skalen liegen.

Fazit

Die Entwicklung eines soliden Verständnisses der linearen Regression erfordert kontinuierliche Übung und Erkundung. Um dein Wissen zu vertiefen, solltest du mehr über den Umgang mit Multikollinearität, Heteroskedastizität und Regularisierungstechniken wie Ridge- und Lasso-Regression lernen. Ein besseres Verständnis der QR-Zerlegung und des Varianzinflationsfaktors kann auch die Modelldiagnose verbessern. Außerdem kann das Verständnis von Normalisierung und Standardisierung die Entscheidungen zur Skalierung von Merkmalen verbessern.