Python, avec son riche écosystème de bibliothèques comme NumPy, statsmodels, et scikit-learn, est devenu le langage de prédilection des data scientists. Sa facilité d'utilisation et sa polyvalence en font un outil idéal pour comprendre les fondements théoriques de la régression linéaire et la mettre en œuvre dans des scénarios réels.
Dans ce guide, je vais vous présenter tout ce que vous devez savoir sur la régression linéaire en Python. Nous commencerons par définir ce qu'est la régression linéaire et pourquoi elle est si importante. Ensuite, nous nous pencherons sur la mécanique, en explorant les équations et les hypothèses sous-jacentes. Vous apprendrez à effectuer des régressions linéaires à l'aide de diverses bibliothèques Python, des calculs manuels avec NumPy aux implémentations rationalisées avec scikit-learn. Nous aborderons la régression linéaire simple et multiple, et je vous montrerai comment évaluer vos modèles et améliorer leurs performances.
Qu'est-ce que la régression linéaire ?
La régression linéaire est une méthode statistique utilisée pour modéliser la relation entre une variable dépendante (cible) et une ou plusieurs variables indépendantes (prédicteurs). L'objectif est de trouver une équation linéaire décrivant au mieux cette relation.
La régression linéaire est largement utilisée pour la modélisation prédictive, les statistiques inférentielles et la compréhension des relations entre les données. Ses applications comprennent la prévision des ventes, l'évaluation des risques et l'analyse de l'impact de différentes variables sur un résultat cible.
Qu'est-ce que la régression linéaire simple ?
Dans le cas d'une régression linéaire simple, l'équation prend la forme d'une ligne dans un espace bidimensionnel ; dans le cas d'une régression linéaire multiple (avec deux variables indépendantes), la relation est représentée par un plan dans un espace tridimensionnel ; pour un nombre encore plus grand de variables indépendantes, l'équation décrit un hyperplan dans un espace à plus haute dimension.
Commençons par un modèle de régression linéaire simple qui, comme je l'ai mentionné, ne comporte qu'une seule variable prédictive. Elle est représentée par l'équation suivante :
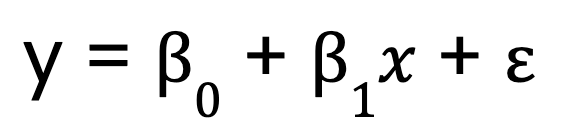
Où ?
- y est la variable dépendante,
- x est la variable indépendante,
- B0 est l'ordonnée à l'origine,
- B1 est le coefficient (pente) de la variable indépendante,
- représente le terme d'erreur.
Qu'est-ce que la régression linéaire multiple ?
En revanche, la régression linéaire multiple étend ce concept à plusieurs variables prédictives :
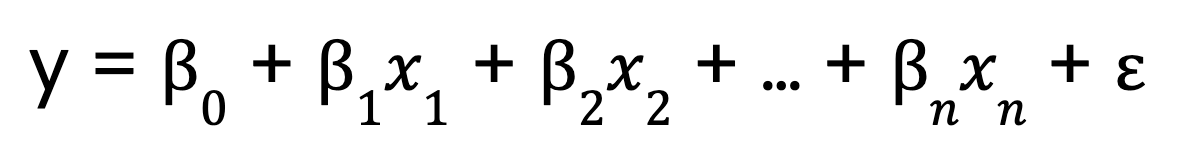
Où ?
- 0 est l'ordonnée à l'origine,
- x1, x2, ..., xn sont les variables prédictives
- 1,2, ..., n sont les coefficients correspondant à chaque variable prédictive,
- est le terme d'erreur.
Les mécanismes de la régression linéaire
Pour comprendre le fonctionnement de la régression linéaire, décomposons ses principaux éléments.
L'équation du modèle linéaire
Nous avons vu ci-dessus les équations de régression linéaire, à la fois avec un prédicteur unique et des prédicteurs multiples. Mais permettez-moi maintenant d'aborder un aspect important des équations.
Le terme "linéaire" dans la régression linéaire fait référence à la forme fonctionnelle du modèle, et pas nécessairement à la forme des données. Plus précisément, cela signifie que
- Le modèle est linéaire dans ses paramètres. Cela signifie que chaque prédicteur est multiplié par un coefficient et additionné.
- La relation entre la variable dépendante et les variables prédictives est additivece qui signifie que les variations de chaque prédicteur ont un effet constant sur la variable dépendante.
- Aucune exponentiation, multiplication entre variables ou transformation non linéaire n'est appliquée aux paramètres. n'est appliquée aux paramètres.
Méthode des moindres carrés ordinaires (MCO)
Pour déterminer la ligne la mieux ajustée, la régression linéaire utilise la méthode des moindres carrés ordinaires (MCO). méthode des moindres carrés ordinaires (MCO) méthode des moindres carrés ordinaires (MCO). Les MCO minimisent la somme des erreurs quadratiques:
Les MCO minimisent la somme des erreurs quadratiques :
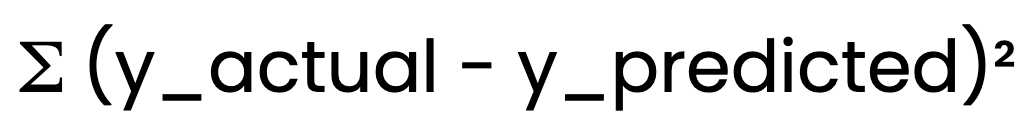
Cela permet de s'assurer que le modèle fournit les meilleures estimations possibles de B0 et de B1.
Hypothèses de la régression linéaire
Pour que la régression linéaire produise des résultats fiables, certaines hypothèses doivent être respectées :
- Linéarité: La relation entre la variable indépendante et la variable dépendante doit être linéaire.
- Indépendance des erreurs: Les résidus (erreurs) ne doivent pas être corrélés entre eux.
- Variance constante (homoscédasticité): La dispersion des résidus doit rester constante pour toutes les valeurs.
- Normalité des résidus: Les résidus doivent suivre une distribution normale.
La validation de ces hypothèses garantit la fiabilité et la validité de notre modèle. Par exemple, si la relation entre les variables n'est pas linéaire, les prévisions du modèle peuvent être inexactes. En cas d'hétéroscédasticité, les intervalles de confiance peuvent être erronés.
Méthodes de régression linéaire en Python
La régression linéaire peut être mise en œuvre dans Python en utilisant différentes approches. Je vous présenterai trois méthodes courantes : les calculs manuels avec NumPy, la modélisation statistique détaillée avec statsmodels et l'apprentissage automatique rationalisé avec scikit-learn.
Approche de calcul manuel (NumPy)
Pour une régression linéaire simple (une variable prédictive), vous pouvez calculer manuellement les paramètres de régression à l'aide de NumPy. Cela implique tout d'abord de calculer la moyenne des variables indépendantes et dépendantes. Nous calculons ensuite la pente (B0) :
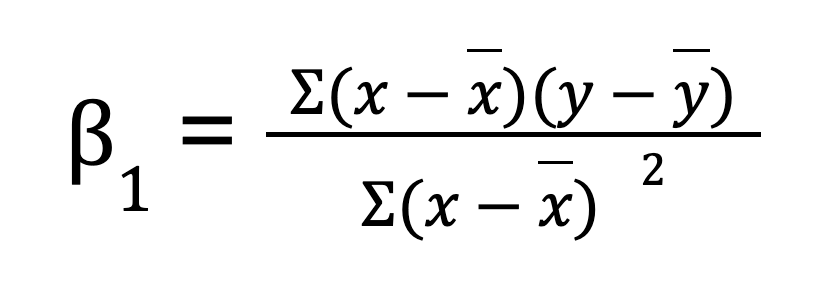
Une fois la pente obtenue, nous pouvons déterminer l'ordonnée à l'origine (B1) :
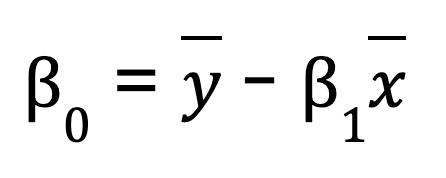
import numpy as np
# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
# Compute means
x_mean = np.mean(x)
y_mean = np.mean(y)
# Compute slope (B1)
B1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean) ** 2)
# Compute intercept (B0)
B0 = y_mean - B1 * x_mean
print(f"Slope (B1): {B1}")
print(f"Intercept (B0): {B0}")
# Predicting values
y_pred = B0 + B1 * x
print("Predicted values:", y_pred)Si vous souhaitez simplifier le processus, NumPy fournit également une fonction intégrée np.polyfit(), qui peut effectuer une régression linéaire pour vous en une seule ligne de code.
# Example of NumPy's polyfit
np.polyfit(x, y, 1) # 1 stands for the degree of the polynomial (linear)Bien que cette méthode soit utile pour comprendre les mathématiques qui sous-tendent la régression linéaire simple, elle n'est pas pratique pour les grands ensembles de données, a moins de précision numérique et ne fonctionne pas pour les problèmes de régression multiple.
Utilisation d'une bibliothèque statistique (statsmodels)
Une manière plus efficace d'effectuer une régression linéaire est d'utiliser statsmodelsune bibliothèque qui fournit des modèles statistiques et des outils d'analyse.
Étapes de l'ajustement d'un modèle des moindres carrés ordinaires (MCO) à l'aide de Statsmodels :
-
Préparez les données: Veillez à ce que la variable indépendante soit structurée correctement.
-
Ajoutez une constante: Cela tient compte du terme d'interception dans l'équation.
-
Adapté au modèle: Utilisez
OLS()à partir destatsmodelspour estimer les paramètres de régression. -
Analysez les résultats: La fonction
.summary()fournit des informations détaillées sur le modèle, notamment les coefficients, les valeurs p et les valeurs R-carré.
import numpy as np
import statsmodels.api as sm
# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
# Add constant for intercept term
X = sm.add_constant(x)
# Fit OLS model
model = sm.OLS(y, X).fit()
# Print summary
print(model.summary())Utilisation d'une bibliothèque d'apprentissage automatique (scikit-learn)
scikit-learn est largement utilisé en raison de sa simplicité, de son évolutivité et de son intégration avec d'autres outils d'apprentissage automatique. Il offre un moyen simple et efficace d'effectuer une régression linéaire à l'aide de la classe LinearRegression .
-
Importez la bibliothèque et chargez votre jeu de données.
-
Reformulez la variable prédictive si nécessaire (pour la régression à une seule variable).
-
Créez une instance de modèle en utilisant
LinearRegression(). -
Ajustez le modèle aux données d'apprentissage.
-
Récupérer les paramètres du modèle: L'attribut
.coeff_renvoie la pente, tandis que.intercept_fournit l'ordonnée à l'origine.
import numpy as np
from sklearn.linear_model import LinearRegression
# Sample data
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # Reshape for scikit-learn
y = np.array([2, 4, 5, 4, 5])
# Create model instance
model = LinearRegression()
# Fit the model
model.fit(x, y)
# Get model parameters
print(f"Slope (B1): {model.coef_[0]}")
print(f"Intercept (B0): {model.intercept_}")
# Predict values
y_pred = model.predict(x)
print("Predicted values:", y_pred)Autres méthodes importantes
Outre NumPy, statsmodels, et scikit-learn, plusieurs autres bibliothèques Python offrent des fonctionnalités de régression :
- Pandas: Utile pour l'analyse exploratoire des données et la modélisation rapide des tendances.
- SciPy: Inclut des fonctions statistiques qui peuvent être utilisées pour l'analyse de régression.
- TensorFlow & PyTorch: Bien qu'ils soient principalement destinés à l'apprentissage profond, ils peuvent traiter efficacement les tâches de régression linéaire.
Chaque approche a ses avantages. Cela dépend de la complexité de votre tâche de régression.
Régression linéaire en Python avec un ou plusieurs prédicteurs
La régression linéaire permet de traiter les relations simples et complexes. Dans cette section, nous allons étudier comment mettre en œuvre la régression linéaire avec un prédicteur (simple) et plusieurs prédicteurs (multiple) à l'aide de Python.
Régression linéaire simple en Python
Pour une régression linéaire simple en Python, nous suivons les étapes suivantes :
Étape 1 : Calculer la corrélation
Le coefficient de corrélation mesure la force de la relation entre x et y. Nous le trouvons en utilisant NumPy :
import numpy as np
# Sample data
x = np.array([1, 2, 3, 4, 5]) # Independent variable
y = np.array([2, 4, 5, 4, 5]) # Dependent variable
correlation = np.corrcoef(x, y)[0, 1]
print("Correlation:", correlation)Étape 2 : Calculez la pente et l'ordonnée à l'origine
La penteB1 est calculée comme suit :
beta_1 = correlation * (np.std(y) / np.std(x))Vous remarquerez peut-être que cette équation est légèrement différente de la précédente, dans laquelle j'ai trouvé la pente en additionnant les produits des écarts entre x et ypuis en divisant cette somme par la somme des carrés des écarts en x. Cette nouvelle méthode, qui utilise la corrélation et l'écart-type, peut sembler différente, mais elle est en fait identique. En réécrivant l'équation précédente, nous pouvons exprimer la pente comme suit r multipliée par le rapport des écarts types de y et de xce qui rend les deux formes algébriquement équivalentes.
Passons maintenant à l'interception :
beta_0 = np.mean(y) - beta_1 * np.mean(x)Étape 3 : Faire des prévisions en utilisant les paramètres calculés
Maintenant que nous avons les coefficients, nous pouvons trouver les valeurs prédites.
y_pred = beta_0 + beta_1 * xJe pense qu'il est utile de passer par ces étapes pour comprendre les calculs sous-jacents avant d'utiliser des bibliothèques telles que scikit-learn.
Régression linéaire multiple en Python
La régression linéaire multiple étend le concept de régression linéaire simple pour modéliser les relations entre une variable dépendante et plusieurs variables indépendantes. Cela nous permet d'analyser des ensembles de données plus complexes où un prédicteur seul n'explique pas suffisamment la variation de la variable dépendante.
Pour effectuer une régression linéaire multiple dans Python, nous utilisons généralement l'algèbre matricielle pour calculer les coefficients qui minimisent la somme des carrés résiduels. Une formule couramment utilisée pour calculer les coefficients dans la régression linéaire multiple est connue sous le nom d'équation normale:
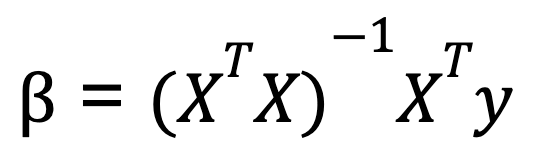
Où ?
- X est la matrice des variables indépendantes (avec une colonne de 1 pour l'ordonnée à l'origine),
- y est le vecteur des valeurs de la variable dépendante.
- XT est la transposée de la matrice de X.
- (XTX)-1 est l'inverse de XTX.
Cette équation donne les valeurs optimales des coefficients qui minimisent la somme des erreurs quadratiques.
Voici un exemple d'exécution d'une régression linéaire multiple avec Python, en utilisant NumPy pour les opérations matricielles :
import numpy as np
# Sample data: two predictors and one dependent variable
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) # Independent variables
y = np.array([6, 8, 9, 11]) # Dependent variable
# Add a column of ones to include the intercept in the model
X = np.column_stack((np.ones(X.shape[0]), X))
# Calculate beta coefficients using the normal equation
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print("Coefficients:", beta)Cette méthode fonctionne bien lorsque les prédicteurs sont indépendants, mais si les prédicteurs sont fortement corrélés, l'inversion de la matrice devient instable. C'est pourquoi des bibliothèques comme scikit-learn utilisent une méthode plus stable numériquement basée sur la décomposition QR pour calculer les coefficients de régression. Ainsi, même si nous pouvons calculer les coefficients à l'aide de l'équation normale, sachez que lorsque nous utilisons la fonction LinearRegression() de scikitlearn, la décomposition qr fonctionne sous le capot.
Traitement de la multicolinéarité
C'est le bon moment pour mentionner une chose qui apparaît comme une préoccupation dans la régression linéaire multiple dans Python. La multicolinéarité se produit lorsque deux variables indépendantes ou plus sont fortement corrélées, ce qui rend difficile l'isolement de leurs effets individuels. Cela peut conduire à des estimations de coefficients instables. Pour détecter et atténuer la multicolinéarité, vous pouvez calculer le facteur d'inflation de la variance (VIF). Vous pouvez également supprimer les variables fortement corrélées ou utiliser des techniques de régularisation telles que la régression ridge et la régression lasso.
Diagnostic et évaluation de modèles de régression linéaire en Python
Après avoir construit votre modèle de régression linéaire, l'étape suivante consiste à évaluer ses performances et à vérifier qu'il répond aux hypothèses sous-jacentes. Cela garantit la fiabilité de vos prévisions et vous aide à identifier les améliorations potentielles.
Analyse résiduelle
L'analyse des résidus est un élément essentiel des diagnostics de régression linéaire. Il permet de vérifier les hypothèses de la régression linéaire et d'identifier toute violation. Les résidus doivent être dispersés de manière aléatoire autour de zéro, sans motif discernable. C'est là que les outils visuels tels que les diagrammes résiduels et les diagrammes Q-Q entrent en jeu :
- Tracé résiduel : Un diagramme de dispersion des résidus par rapport aux valeurs prédites (ou variables indépendantes) permet de vérifier s'il existe une relation que le modèle n'a pas prise en compte. Dans l'idéal, le graphique devrait montrer une répartition aléatoire sans schéma clair, ce qui suggère que le modèle a bien capturé la relation linéaire.
- Graphique Q-Q (Graphique Quantile-Quantile) : Un graphique Q-Q permet d'évaluer si les résidus suivent une distribution normale. Pour que la régression linéaire soit valable, les résidus doivent être approximativement distribués normalement. Une ligne droite sur le graphique Q-Q indique la normalité.
En Python, nous pouvons créer ces tracés facilement avec des bibliothèques comme matplotlib, seaborn, et statsmodels.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
# Sample data and linear regression model
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) # Independent variables
y = np.array([6, 8, 9, 11]) # Dependent variable
# Add an intercept term
X = sm.add_constant(X)
# Fit the linear regression model
model = sm.OLS(y, X).fit()
# Get the residuals
residuals = model.resid
# 1. Residual Plot
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
# 2. Q-Q Plot
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line ='45', ax=plt.gca())
plt.title('Q-Q Plot')
plt.tight_layout()
plt.show()Mesures d'évaluation
Outre l'analyse visuelle, les mesures quantitatives sont essentielles pour évaluer l'adéquation du modèle de régression linéaire aux données. Voici quelques mesures d'évaluation clés :
- R-carré (R²) : Cette mesure vous indique dans quelle mesure la variance de la variable dépendante peut être expliquée par les variables indépendantes. Une valeur R² proche de 1 indique que le modèle explique une grande partie de la variance, tandis qu'une valeur proche de 0 signifie que le modèle ne s'ajuste pas bien aux données.
- R-carré ajusté: Cette métrique ajuste le R² en fonction du nombre de prédicteurs dans le modèle. Il est utile pour comparer des modèles avec différents nombres de prédicteurs.
- Erreur quadratique moyenne (RMSE) : Le RMSE mesure l'ampleur moyenne des erreurs dans les prédictions du modèle, avec les mêmes unités que la variable dépendante. Un RMSE plus faible indique une meilleure performance prédictive.
- Erreur absolue moyenne (EAM) : La MAE mesure l'ampleur moyenne des erreurs dans les prédictions du modèle, mais contrairement à la RMSE, elle ne pénalise pas aussi lourdement les erreurs importantes. Elle est plus facile à interpréter car elle est exprimée dans les mêmes unités que la variable dépendante.
Ces métriques peuvent être facilement calculées en Python à l'aide de statsmodels ou scikit-learn:
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np
# Make predictions using the model
y_pred = model.predict(X)
# R-squared
r_squared = r2_score(y, y_pred)
print("R-squared:", r_squared)
# Adjusted R-squared (calculated manually)
n = len(y) # number of data points
p = X.shape[1] - 1 # number of predictors (excluding intercept)
adj_r_squared = 1 - (1 - r_squared) * (n - 1) / (n - p - 1)
print("Adjusted R-squared:", adj_r_squared)
# RMSE
rmse = np.sqrt(mean_squared_error(y, y_pred))
print("Root Mean Squared Error (RMSE):", rmse)
# MAE
mae = mean_absolute_error(y, y_pred)
print("Mean Absolute Error (MAE):", mae)En évaluant ces paramètres, vous obtenez des informations sur la précision du modèle, la qualité de l'ajustement et la capacité du modèle à s'adapter à de nouvelles données.
Améliorer votre modèle de régression
Une fois que vous avez évalué votre modèle de régression linéaire, l'étape suivante consiste à explorer les moyens d'améliorer ses performances. Une approche courante consiste à utiliser lesite pourtransformer les caractéristiques, ce qui permet de traiter les relations non linéaires et d'aider le modèle à mieux saisir les modèles sous-jacents dans les données.
Transformations des caractéristiques
Rappelez-vous que, dans la régression linéaire, le modèle suppose une relation linéaire entre les variables indépendantes (prédicteurs) et la variable dépendante. Cependant, de nombreux ensembles de données du monde réel présentent des relations non linéaires qu'un simple modèle linéaire peut ne pas bien saisir. En appliquant des transformations de caractéristiques, telles que des transformations logarithmiques ou de racine carrée, vous pouvez parfois améliorer les performances du modèle.
Transformation logarithmique
Cette méthode est souvent utilisée lorsqu'une caractéristique présente une croissance exponentielle ou de grandes valeurs positives. Par exemple, la transformation de données sur les revenus très asymétriques (où quelques valeurs de revenus très élevés dominent) peut rendre la distribution plus normale.
import numpy as np
df['log_income'] = np.log(df['income'] + 1) # +1 to avoid log(0)Transformation de la racine carrée
Cette fonction est utile pour les caractéristiques qui suivent une relation quadratique. Par exemple, une caractéristique qui représente des chiffres (comme le nombre de visites sur un site web) peut bénéficier d'une transformation en racine carrée.
df['sqrt_visits'] = np.sqrt(df['visits'])En transformant ces caractéristiques, vous aidez le modèle à mieux saisir les relations que l'approche linéaire n'a pas permis de mettre en évidence. L'essentiel est de tester différentes transformations et d'observer l'effet sur la performance du modèle. Il ne s'agit pas d'une approche unique, qui nécessite des tests empiriques. des tests empiriques.
Normalisation et standardisation
Outre les transformations de caractéristiques, il est également important de comprendre l'impact de la normalisation et de la standardisation sur votre modèle de régression, en particulier lorsque vous avez affaire à des caractéristiques ayant des unités ou des échelles différentes. La normalisation remet à l'échelle les valeurs des caractéristiques dans une plage, généralement [0, 1]. La normalisation redimensionne les caractéristiques pour obtenir une moyenne de 0 et un écart-type de 1.
Lorsque vous avez plusieurs prédicteurs, la normalisation ou la standardisation des données permet d'interpréter les coefficients de manière plus significative. En d'autres termes, t permet de montrer dans quelle mesure chaque variable prédictive contribue à la variable dépendante par rapport aux autres variables prédictives. Ceci est particulièrement utile lorsque les prédicteurs se situent sur des échelles différentes.
Conclusion
Le développement d'une bonne compréhension de la régression linéaire nécessite une pratique et une exploration continues. Pour approfondir vos connaissances, envisagez d'en apprendre davantage sur la gestion de la multicollinéarité, de l'hétéroscédasticité et des techniques de régularisation telles que la régression Ridge et Lasso. Une meilleure compréhension de la décomposition QR et du facteur d'inflation de la variance peut également améliorer le diagnostic des modèles. En outre, la compréhension de la normalisation par rapport à la standardisation peut améliorer les décisions de mise à l'échelle des caractéristiques.
Devenez un scientifique ML
Professionnel expérimenté des données et écrivain passionné par l'autonomisation des experts en herbe dans le domaine des données.
