Regressão linear em Python: Seu guia para modelagem preditiva

O Python, com seu rico ecossistema de bibliotecas, como NumPy, statsmodels e scikit-learn, tornou-se a linguagem preferida dos cientistas de dados. Sua facilidade de uso e versatilidade o tornam perfeito tanto para compreender os fundamentos teóricos da regressão linear quanto para implementá-la em cenários do mundo real.

Neste guia, mostrarei tudo o que você precisa saber sobre regressão linear em Python. Começaremos definindo o que é regressão linear e por que ela é tão importante. Em seguida, analisaremos a mecânica, explorando as equações e suposições subjacentes. Você aprenderá a realizar a regressão linear usando várias bibliotecas Python, desde cálculos manuais com o NumPy até implementações simplificadas com o scikit-learn. Abordaremos a regressão linear simples e múltipla, e mostrarei a você como avaliar seus modelos e aprimorar seu desempenho.

O que é regressão linear?

A regressão linear é um método estatístico usado para modelar a relação entre uma variável dependente (alvo) e uma ou mais variáveis independentes (preditores). O objetivo é encontrar uma equação linear que melhor descreva essa relação.

A regressão linear é amplamente usada para modelagem preditiva, estatística inferencial e compreensão das relações nos dados. Suas aplicações incluem a previsão de vendas, a avaliação de riscos e a análise do impacto de diferentes variáveis em um resultado desejado.

O que é regressão linear simples?

Para a regressão linear simples, isso assumiria a forma de uma linha no espaço bidimensional; para a regressão linear múltipla (com duas variáveis independentes), a relação é representada por um plano no espaço tridimensional; para um número ainda maior de variáveis independentes, a equação descreve um hiperplano no espaço de dimensão superior.

Vamos começar com um modelo de regressão linear simples, que, como mencionei, tem apenas uma variável preditora. Ela é representada por esta equação:

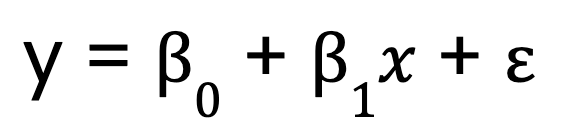
Onde:

• y é a variável dependente,
• x é a variável independente,
• _B0 é a interceptação,
• _B1 é o coeficiente (inclinação) da variável independente,
• representa o termo de erro.

O que é regressão linear múltipla?

Por outro lado, a regressão linear múltipla amplia esse conceito para incluir várias variáveis preditoras:

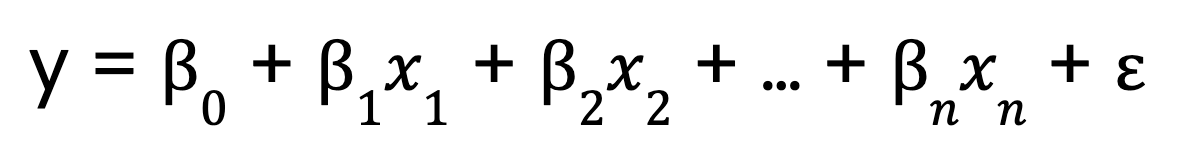
Onde:

• 0 é a interceptação,
• x₁, x₂, ..., x_n são as variáveis preditoras
• 1,2, ..., n são os coeficientes correspondentes a cada variável preditora,
• é o termo de erro.

A mecânica por trás da regressão linear

Para que você entenda como funciona a regressão linear, vamos detalhar seus principais componentes.

A equação do modelo linear

Vimos equações para regressão linear, acima, tanto com um único preditor quanto com vários preditores. Mas agora, deixe-me falar sobre um aspecto importante das equações. 

O termo linear na regressão linear refere-se à forma funcional do modelo, não necessariamente à forma dos dados. Especificamente, isso significa que:

1. O modelo é linear em seus parâmetros. Isso significa que cada preditor é multiplicado por um coeficiente e somado.
2. A relação entre a variável dependente e os preditores é aditivaou seja, as alterações em cada preditor têm um efeito consistente sobre a variável dependente.
3. Nenhuma exponenciação, multiplicação entre variáveis ou transformações não lineares são aplicadas aos parâmetros.

Método dos mínimos quadrados ordinários (OLS)

Para determinar a linha de melhor ajuste, a regressão linear usa o método mínimos quadrados ordinários (OLS) (OLS). O OLS minimiza a soma dos erros ao quadrado:

O OLS minimiza a soma dos erros ao quadrado:

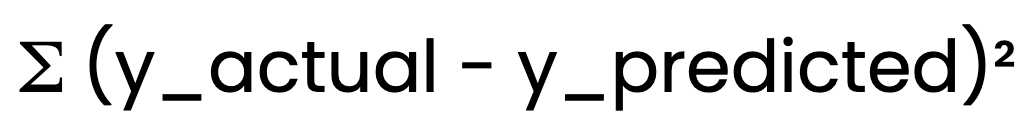
Isso garante que o modelo forneça as melhores estimativas possíveis de B₀ e B₁.

Pressupostos da regressão linear

Para que a regressão linear produza resultados confiáveis, é necessário atender a determinadas premissas:

1. Linearidade: A relação entre a variável independente e a dependente deve ser linear.
2. Independência dos erros: Os resíduos (erros) não devem estar correlacionados entre si.
3. Variância constante (homocedasticidade): A dispersão dos resíduos deve permanecer constante em todos os valores.
4. Normalidade dos resíduos: Os resíduos devem seguir uma distribuição normal.

A validação dessas suposições garante que nosso modelo seja confiável e válido. Por exemplo, se a relação entre as variáveis não for linear, as previsões do modelo podem ser imprecisas. Se houver heterocedasticidade, os intervalos de confiança podem estar errados.

Maneiras de fazer regressão linear em Python

A regressão linear pode ser implementada em Python usando diferentes abordagens. Vou mostrar a você três métodos comuns: cálculos manuais com NumPy, modelagem estatística detalhada com statsmodels e machine learning simplificado com scikit-learn.

Abordagem de cálculo manual (NumPy)

Para uma regressão linear simples (uma variável preditora), você pode calcular manualmente os parâmetros de regressão usando o NumPy. Isso envolve primeiro o cálculo da média das variáveis independentes e dependentes. Em seguida, calculamos a inclinação (_B0):

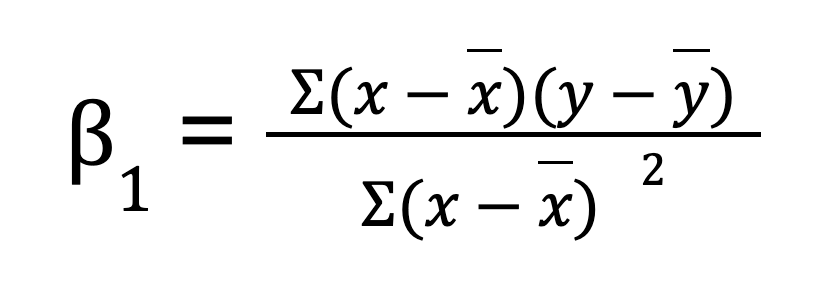
Quando tivermos a inclinação, poderemos determinar a interceptação (_B1):

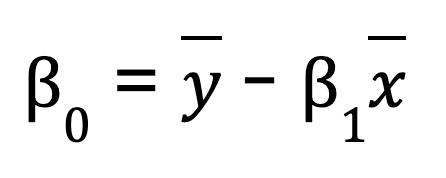
import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Compute means
x_mean = np.mean(x)
y_mean = np.mean(y)

# Compute slope (B1)
B1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean) ** 2)

# Compute intercept (B0)
B0 = y_mean - B1 * x_mean

print(f"Slope (B1): {B1}")
print(f"Intercept (B0): {B0}")

# Predicting values
y_pred = B0 + B1 * x
print("Predicted values:", y_pred)

Se você estiver interessado em simplificar o processo, o NumPy também oferece uma função integrada np.polyfit(), que pode executar a regressão linear para você com apenas uma linha de código.

# Example of NumPy's polyfit
np.polyfit(x, y, 1)  # 1 stands for the degree of the polynomial (linear)

Embora esse método seja útil para você entender a matemática por trás da regressão linear simples, ele não é prático para grandes conjuntos de dados, tem menos precisão numérica e não funciona para problemas de regressão múltipla.

Usando uma biblioteca estatística (statsmodels)

Uma maneira mais eficiente de realizar a regressão linear é usar o statsmodelsuma biblioteca que fornece modelos estatísticos e ferramentas de análise.

Etapas para ajustar um mínimos quadrados ordinários (OLS) usando o Statsmodels:

1. Prepare os dados: Certifique-se de que a variável independente esteja estruturada adequadamente.

2. Adicione uma constante: Isso leva em conta o termo de interceptação na equação.

3. Ajuste o modelo: Use OLS() de statsmodels para estimar os parâmetros de regressão.

4. Analise os resultados: A função .summary() fornece informações detalhadas sobre o modelo, incluindo coeficientes, valores de p e valores de R-quadrado.

import numpy as np
import statsmodels.api as sm

# Sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])

# Add constant for intercept term
X = sm.add_constant(x)

# Fit OLS model
model = sm.OLS(y, X).fit()

# Print summary
print(model.summary())

Usando uma biblioteca de machine learning (Scikit-Learn)

scikit-learn é amplamente utilizado devido à sua simplicidade, escalabilidade e integração com outras ferramentas de machine learning. Ele oferece uma maneira simples e eficiente de realizar a regressão linear usando a classe LinearRegression.

1. Importe a biblioteca e carregue seu conjunto de dados.

2. Remodele a variável preditora se necessário (para regressão de variável única).

3. Criar uma instância de modelo usando LinearRegression().

4. Ajuste o modelo aos dados de treinamento.

5. Recupere os parâmetros do modelo: O atributo .coeff_ retorna a inclinação, enquanto .intercept_ fornece a interceptação.

import numpy as np
from sklearn.linear_model import LinearRegression

# Sample data
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)  # Reshape for scikit-learn
y = np.array([2, 4, 5, 4, 5])

# Create model instance
model = LinearRegression()

# Fit the model
model.fit(x, y)

# Get model parameters
print(f"Slope (B1): {model.coef_[0]}")
print(f"Intercept (B0): {model.intercept_}")

# Predict values
y_pred = model.predict(x)
print("Predicted values:", y_pred)

Outros métodos importantes

Além de NumPy, statsmodels e scikit-learn, várias outras bibliotecas Python fornecem recursos de regressão:

• Pandas: Útil para análise exploratória de dados e modelagem rápida de tendências.
• SciPy: Inclui funções estatísticas que podem ser usadas para análise de regressão.
• TensorFlow & PyTorch: Embora sejam principalmente para aprendizagem profunda, eles podem lidar com tarefas de regressão linear de forma eficaz.

Cada abordagem tem suas vantagens, dependendo da complexidade da sua tarefa de regressão e do nível de análise necessário.

Regressão linear em Python com um ou mais preditores

A regressão linear pode lidar com relacionamentos simples e complexos. Nesta seção, exploraremos como implementar a regressão linear com um preditor (simples) e vários preditores (múltiplos) usando Python.

Regressão linear simples em Python

Para uma regressão linear simples em Python, você deve seguir estas etapas:

Etapa 1: Calcule a correlação

O coeficiente de correlação mede a força da relação entre x e y. Nós o encontramos usando o NumPy:

import numpy as np

# Sample data
x = np.array([1, 2, 3, 4, 5])  # Independent variable
y = np.array([2, 4, 5, 4, 5])  # Dependent variable

correlation = np.corrcoef(x, y)[0, 1]
print("Correlation:", correlation)

Etapa 2: Calcule a inclinação e a interceptação

A inclinação _B1 é calculada como:

beta_1 = correlation * (np.std(y) / np.std(x))

Você pode notar que essa equação parece um pouco diferente da anterior, em que encontrei a inclinação somando os produtos dos desvios entre $x$ e ye, em seguida, dividindo pela soma dos desvios ao quadrado em $x$. Esse novo método, que usa a correlação e o desvio padrão, pode parecer diferente, mas na verdade é o mesmo.

O coeficiente de correlação $r$ é calculado como a soma dos produtos das diferenças da média, dividida pela raiz quadrada do produto da soma das diferenças ao quadrado em $x$ e $y$. Ao reescrever a equação anterior, podemos expressar a inclinação como $r$ multiplicado pela razão dos desvios padrão de $y$ e $x$tornando as duas formas algebricamente equivalentes.

Agora, quanto à interceptação:

beta_0 = np.mean(y) - beta_1 * np.mean(x)

Etapa 3: Fazer previsões usando os parâmetros computados

Agora que temos os coeficientes, podemos encontrar os valores previstos.

y_pred = beta_0 + beta_1 * x

Acredito que passar por essas etapas seja útil para que você entenda os cálculos subjacentes antes de usar bibliotecas como scikit-learn.

Regressão linear múltipla em Python

A regressão linear múltipla amplia o conceito de regressão linear simples para modelar as relações entre uma variável dependente e várias variáveis independentes. Isso nos permite analisar conjuntos de dados mais complexos em que um preditor sozinho não explica suficientemente a variação na variável dependente.

Para realizar a regressão linear múltipla em Python, normalmente usamos a álgebra matricial para calcular os coeficientes que minimizam a soma residual dos quadrados. Uma fórmula comumente ensinada para calcular os coeficientes na regressão linear múltipla é conhecida como equação normal:

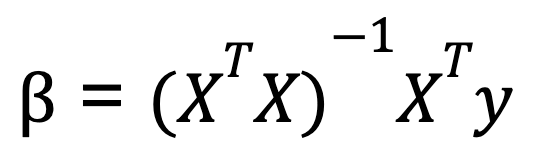
Onde:

• X é a matriz de variáveis independentes (com uma coluna de uns para a interceptação),
• y é o vetor de valores da variável dependente.
• X^T é a transposição da matriz de X.
• (X^TX)^-1 é o inverso de X^TX.

Essa equação fornece os valores ideais para os coeficientes que minimizam a soma dos erros quadrados.

Aqui está um exemplo de regressão linear múltipla com Python, usando NumPy para as operações de matriz:

import numpy as np

# Sample data: two predictors and one dependent variable
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add a column of ones to include the intercept in the model
X = np.column_stack((np.ones(X.shape[0]), X))

# Calculate beta coefficients using the normal equation
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print("Coefficients:", beta)

Esse método funciona bem quando os preditores são independentes, mas se os preditores forem altamente correlacionados, a inversão da matriz se tornará instável. Por esse motivo, bibliotecas como scikit-learn usam um método numericamente mais estável, baseado na decomposição QR. baseado na decomposição QR para calcular os coeficientes degressão. Portanto, mesmo que possamos calcular os coeficientes usando a equação normal, saiba que, quando usamos a função LinearRegression() de scikitlearn, a decomposição qr está funcionando nos bastidores.

Como lidar com a multicolinearidade

Agora é um bom momento para você mencionar uma coisa que aparece como uma preocupação na regressão linear múltipla em Python. A multicolinearidade ocorre quando duas ou mais variáveis independentes estão altamente correlacionadas, dificultando o isolamento de seus efeitos individuais. Isso pode levar a estimativas de coeficiente instáveis. Para detectar e atenuar a multicolinearidade, você pode calcular o fator de inflação de variância (VIF). Você também pode remover variáveis altamente correlacionadas ou usar técnicas de regularização, como regressão de cumeeira e regressão de laço.

Diagnóstico e avaliação de modelos de regressão linear em Python

Depois de criar seu modelo de regressão linear, a próxima etapa é avaliar seu desempenho e validar se ele atende às premissas subjacentes. Isso garante a confiabilidade das suas previsões e ajuda você a identificar possíveis melhorias.

Análise residual

A análise residual é uma parte essencial dos diagnósticos de regressão linear. Ele ajuda a verificar as suposições da regressão linear e a identificar quaisquer violações. Os resíduos devem ser dispersos aleatoriamente em torno de zero, sem nenhum padrão discernível. É aqui que as ferramentas visuais, como gráficos residuais e gráficos Q-Q, entram em ação:

1. Gráfico residual: Um gráfico de dispersão dos resíduos em relação aos valores previstos (ou variáveis independentes) ajuda a verificar se há alguma relação que o modelo não tenha levado em conta. O ideal é que o gráfico mostre uma dispersão aleatória sem um padrão claro, o que sugere que o modelo captou bem a relação linear.
2. Gráfico Q-Q (Gráfico de Quantil-Quantil): Um gráfico Q-Q ajuda a avaliar se os resíduos seguem uma distribuição normal. Para que a regressão linear seja válida, os resíduos devem ser aproximadamente distribuídos normalmente. Uma linha reta no gráfico Q-Q indica normalidade.

Em Python, podemos criar esses gráficos facilmente com bibliotecas como matplotlib, seaborn e statsmodels.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# Sample data and linear regression model
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])  # Independent variables
y = np.array([6, 8, 9, 11])  # Dependent variable

# Add an intercept term
X = sm.add_constant(X)

# Fit the linear regression model
model = sm.OLS(y, X).fit()

# Get the residuals
residuals = model.resid

# 1. Residual Plot
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')

# 2. Q-Q Plot
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line ='45', ax=plt.gca())
plt.title('Q-Q Plot')

plt.tight_layout()
plt.show()

Métricas de avaliação

Além da análise visual, as métricas quantitativas são essenciais para avaliar a adequação do modelo de regressão linear aos dados. Algumas das principais métricas de avaliação incluem:

1. R-quadrado (R²): Essa métrica informa a você quanto da variação na variável dependente pode ser explicada pelas variáveis independentes. Um valor de R² próximo de 1 indica que o modelo explica uma grande proporção da variação, enquanto um valor próximo de 0 significa que o modelo não se ajusta bem aos dados.
2. R-quadrado ajustado: Essa métrica ajusta o R² para o número de preditores no modelo. É útil para comparar modelos com diferentes números de preditores.
3. Raiz do erro quadrático médio (RMSE): O RMSE mede a magnitude média dos erros nas previsões do modelo, com as mesmas unidades da variável dependente. Um RMSE menor indica melhor desempenho preditivo.
4. Erro absoluto médio (MAE): O MAE mede a magnitude média dos erros nas previsões do modelo, mas, diferentemente do RMSE, não penaliza tanto os erros grandes. É mais fácil de interpretar, pois está nas mesmas unidades que a variável dependente.

Essas métricas podem ser facilmente calculadas em Python usando statsmodels ou scikit-learn:

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

# Make predictions using the model
y_pred = model.predict(X)

# R-squared
r_squared = r2_score(y, y_pred)
print("R-squared:", r_squared)

# Adjusted R-squared (calculated manually)
n = len(y)  # number of data points
p = X.shape[1] - 1  # number of predictors (excluding intercept)
adj_r_squared = 1 - (1 - r_squared) * (n - 1) / (n - p - 1)
print("Adjusted R-squared:", adj_r_squared)

# RMSE
rmse = np.sqrt(mean_squared_error(y, y_pred))
print("Root Mean Squared Error (RMSE):", rmse)

# MAE
mae = mean_absolute_error(y, y_pred)
print("Mean Absolute Error (MAE):", mae)

Ao avaliar essas métricas, você obtém insights sobre a precisão do modelo, a qualidade do ajuste e a capacidade de generalização do modelo para novos dados.

Aprimorando seu modelo de regressão

Depois que você avaliar seu modelo de regressão linear, a próxima etapa é explorar maneiras de melhorar seu desempenho. Uma abordagem comum é por meio de transformações de recursos, que podem tratar de relações não lineares e ajudar o modelo a capturar melhor os padrões subjacentes nos dados.

Transformações de recursos

Lembre-se de que, na regressão linear, o modelo pressupõe uma relação linear entre as variáveis independentes (preditoras) e a variável dependente. No entanto, muitos conjuntos de dados do mundo real têm relações não lineares que um modelo linear simples pode não capturar bem. Ao aplicar transformações de recursos, como transformações logarítmicas ou de raiz quadrada, você pode, às vezes, melhorar o desempenho do modelo.

Transformação logarítmica

Isso geralmente é usado quando um recurso apresenta crescimento exponencial ou tem grandes valores positivos. Por exemplo, a transformação de dados de renda altamente distorcidos (em que predominam alguns valores de renda muito alta) pode tornar a distribuição mais normal.

import numpy as np
df['log_income'] = np.log(df['income'] + 1)  # +1 to avoid log(0)

Transformação da raiz quadrada

Isso é útil para recursos que seguem uma relação quadrática. Por exemplo, um recurso que representa contagens (como o número de visitas a um site) pode se beneficiar de uma transformação de raiz quadrada.

df['sqrt_visits'] = np.sqrt(df['visits'])

Ao transformar esses recursos, você está ajudando o modelo a capturar melhor as relações que antes não eram percebidas pela abordagem linear. A chave é testar diferentes transformações e observar o efeito no desempenho do modelo. Não se trata de uma abordagem única para todos os casos e requer testes empíricos.

Normalização e padronização

Além das transformações de recursos, também é importante entender o impacto da normalização e da padronização no seu modelo de regressão, especialmente quando você está lidando com recursos que têm unidades ou escalas diferentes. A normalização redimensiona os valores dos recursos para um intervalo, normalmente [0, 1]. A padronização redimensiona os recursos para que tenham uma média de 0 e um desvio padrão de 1.

Quando você tem vários preditores, normalizar ou padronizar os dados ajuda a interpretar os coeficientes de forma mais significativa. Ou seja, ajuda a mostrar o quanto cada variável preditora contribui para a variável dependente em relação a outros preditores. Isso é especialmente útil quando os preditores estão em escalas diferentes.

Conclusão

O desenvolvimento de uma sólida compreensão da regressão linear requer prática e exploração contínuas. Para aprofundar seu conhecimento, considere a possibilidade de aprender mais sobre como lidar com a multicolinearidade, a heterocedasticidade e as técnicas de regularização, como a regressão Ridge e Lasso. Se você entender melhor a decomposição QR e o fator de inflação da variância, também poderá aprimorar o diagnóstico do modelo. Além disso, entender a normalização versus a padronização pode melhorar as decisões de dimensionamento de recursos.