Triangle Inequality: From Geometry to Machine Learning

The triangle inequality theorem tells us that in any triangle, the total length of any two sides must always be greater than or equal to the length of the side that’s left. This basic geometric principle extends far beyond triangles, becoming an essential concept in mathematics, computer science, and data analysis.

In this article, we'll explore the triangle inequality from its basic definition to its advanced applications, showing how this straightforward concept continues to shape our approach to solving complex problems across diverse fields.

What Is the Triangle Inequality?

The triangle inequality states that for any triangle with sides of length a, b, and c, the following three inequalities must always hold:

• a + b ≥ c
• a + c ≥ b
• b + c ≥ a

This means that the sum of the lengths of any two sides of a triangle must always be greater than or equal to the length of the third side. If you think about it intuitively, this makes sense: you cannot form a triangle if one side is longer than the sum of the other two sides.

When equality occurs in any of these conditions (for example, if a + b = c), the triangle "degenerates" into a straight line. In this case, the three points that would form the vertices of the triangle all lie on the same line, with one point between the other two.

The triangle inequality isn't just a rule for triangles in Euclidean geometry. It represents a broader mathematical concept that extends to many other mathematical structures:

• In vector spaces, it takes the form ||u + v|| ≤ ||u|| + ||v||, where ||u|| represents the norm (or length) of vector u.
• For real numbers, it simplifies to the absolute value inequality |a + b| ≤ |a| + |b|.
• In metric spaces, it defines one of the core properties of distance functions.

These generalizations make the triangle inequality one of the most versatile and important concepts in mathematics, with applications ranging from basic geometry to advanced machine learning algorithms.

Note on degenerate triangles

In this article, we use the “greater than or equal to” (≥) form of the triangle inequality to include what are known as degenerate triangles. Degenerate triangles are cases where the sum of two side lengths exactly equals the third. 

These don’t look like triangles in the everyday sense because they are flat and have zero area and collinear points. To someone who is especially interested in math, however, these degenerate triangles are still valid as triangles and are important in limits and proofs. So I’ve left the ≥ to account for the limiting cases. This is referred to as "the triangle inequality in its non-strict form."

Geometric Proof of the Triangle Inequality

The triangle inequality has several elegant proofs, with one of the most famous dating back to Euclid's Elements (Book 1, Proposition 20). Here's how we can understand the proof geometrically:

Consider a triangle with sides of lengths x, y, and z. To prove that z ≤ x + y, we can use the concept that the shortest distance between two points is a straight line.

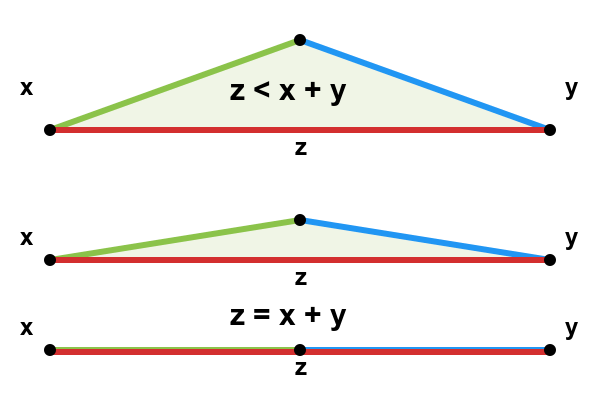
From proper triangle to collinear points. Image by Author

As illustrated above, we can see how the relationship between sides changes as the triangle's shape changes. In a proper triangle (top), the length of one side (z) is strictly less than the sum of the other two sides (x + y). As the middle vertex moves toward the line connecting the other two vertices (middle image), the sum x + y gets closer to equaling z. In the limiting case (bottom image), when all three points become collinear, we reach the equality case where z = x + y.

This intuitive understanding aligns with the fundamental principle that the shortest distance between two points is a straight line. If we label the three vertices of our triangle as points, the direct path from one vertex to another along side z must be shorter than taking the detour along sides x and y combined.

A more formal proof using the Law of Cosines provides additional insight:

• The Law of Cosines states that z^² = x^² + y^² - 2xy·cos(θ), where θ is the angle between sides x and y
• Since cos(θ) is at most 1 (when angle C is 0°), we have:
• z^² ≤ x^² + y^² - 2xy = (x - y)^²
• Taking the square root: z ≤ |x - y|
• This means z ≤ x + y (the triangle inequality)

For right triangles, the Pythagorean theorem gives us another angle:

• In a right triangle, z^² = x^² + y^²
• This means z = √(x^² + y^²)
• Since √(x^² + y^²) < x + y for positive x and y, we again have z < x + y

The intuitive explanation is particularly illuminating: to travel from one point to another, taking a direct route (along side z) is always shorter than taking a detour through a third point (traveling along sides x and y). This observation lies at the heart of the triangle inequality and explains why it's such a fundamental concept in distance calculations.

Triangle Inequality in Vector Spaces

The triangle inequality extends naturally beyond Euclidean geometry into the realm of vector spaces, where it becomes a fundamental property of vector norms. In this context, the inequality states that for any vectors u and v in a vector space:

||u + v|| ≤ ||u|| + ||v||

This means that the norm (or length) of the sum of two vectors is at most equal to the sum of their individual norms. This property is essential for any function to qualify as a norm in vector spaces.

The most familiar special case occurs with real numbers, which can be viewed as vectors in a one-dimensional space. Here, the triangle inequality simplifies to the absolute value inequality:

|a + b| ≤ |a| + |b|

This fundamental property applies across different types of norms in vector spaces:

• Euclidean norm (L²-norm): This is the standard distance measure in Euclidean space, calculated as the square root of the sum of squared components. For vectors in ℝⁿ, the triangle inequality confirms that the straight-line distance between points is shorter than the sum of other path segments.
• Taxicab norm (L¹-norm): Also known as the Manhattan distance, this norm sums the absolute differences of the vectors' components. Even though paths may look different in this geometry (moving along grid lines rather than diagonally), the triangle inequality still holds.
• p-norms: More generally, the triangle inequality holds for all p-norms, where p ≥ 1. These are defined as ||x||ₚ = (∑|xᵢ|ᵖ)^(1/p).

The proof of the triangle inequality for vector norms often uses the Cauchy-Schwarz inequality or Minkowski's inequality, depending on the specific norm being considered.

This vector space formulation of the triangle inequality is particularly important in machine learning and data science, where norms are used to measure distances between data points, calculate errors, and define similarity metrics. Understanding how the triangle inequality constrains these distances provides the mathematical foundation for many clustering algorithms, dimensionality reduction techniques, and optimization methods.

Triangle Inequality in Metric Spaces

The triangle inequality takes on a foundational role in metric spaces, where it serves as one of the defining axioms for the concept of distance. A metric space consists of a set of points together with a distance function (or metric) that quantifies how far apart any two points are from each other.

For a function d to qualify as a metric on a set X, it must satisfy three key properties for all points x, y, and z in X:

1. Non-negativity and identity: d(x, y) ≥ 0, with d(x, y) = 0 if and only if x = y
2. Symmetry: d(x, y) = d(y, x)
3. Triangle inequality: d(x, z) ≤ d(x, y) + d(y, z)

The triangle inequality in this context states that the distance from point x to point z is never greater than the sum of the distance from x to some intermediate point y and the distance from y to z. This property ensures that the "direct path" between two points is always the shortest.

This property has profound implications in the study of metric spaces:

• Convergence of sequences: The triangle inequality is essential for proving that limits of sequences in metric spaces are unique. If a sequence converges to two different points, the triangle inequality would be violated.
• Continuity of functions: When proving that a function between metric spaces is continuous, the triangle inequality is used to establish the relationship between the distances in the domain and codomain.
• Reverse triangle inequality: A useful corollary states that |d(x, z) - d(y, z)| ≤ d(x, y). This inequality helps bound the difference between distances from two points to a third point.

The reverse triangle inequality is particularly valuable in computational geometry and machine learning, as it allows for efficient pruning of search spaces. For example, in k-nearest neighbor algorithms, it helps eliminate candidates without having to compute all pairwise distances.

Metric spaces provide a generalized framework for studying many mathematical structures. Euclidean spaces, function spaces, and discrete spaces can all be viewed as metric spaces, each with their own distance function satisfying the triangle inequality. This unifying perspective demonstrates why the triangle inequality appears so frequently across different branches of mathematics and its applications.

Generalizations and Extensions

The triangle inequality extends beyond its basic formulation for triangles, finding applications in more complex geometric structures and specialized mathematical frameworks.

Polygon inequality

A natural generalization of the triangle inequality applies to polygons with more than three sides. For any n-sided polygon:

• The sum of the lengths of any n-1 sides must be greater than the length of the remaining side.

This can be understood intuitively: to form a closed polygon, you cannot have one side that is longer than all the others combined. This generalization has applications in computational geometry, particularly in polygon construction algorithms and mesh generation for computer graphics and scientific simulations.

Higher-dimensional simplices

The triangle inequality concept extends to higher-dimensional simplices—generalizations of triangles in higher dimensions:

• A 3D simplex is a tetrahedron
• A 4D simplex is a 5-cell (or pentachoron)
• And so on for higher dimensions

In each case, similar inequality constraints apply to the edges of these structures. These constraints are important in high-dimensional data analysis, where they help define the boundaries of valid configurations in feature spaces.

Special cases in non-Euclidean geometries

Interestingly, in some non-Euclidean geometries, the nature of the triangle inequality changes:

• In Minkowski space, used in the mathematics of special relativity, certain distance measures (spacetime intervals) can lead to a reversed triangle inequality for timelike separations. This means that in some cases, the sum of two sides can be less than the third side.
• In hyperbolic geometry, triangles have angle sums less than 180 degrees, and the triangle inequality becomes stricter than in Euclidean space.
• In spherical geometry (like on the surface of the Earth), the shortest path between two points is a great circle. The triangle inequality still holds, but with interesting consequences for navigation and distance calculation.

These specialized versions of the triangle inequality are crucial in theoretical physics, particularly in general relativity, where the geometry of spacetime determines the paths of objects and light.

Implications for information theory

The triangle inequality also appears in information theory and statistics:

• Some divergence measures, which quantify the difference between probability distributions, satisfy triangle inequality-like properties
• These properties enable the development of efficient algorithms for comparing and clustering distributions

Understanding these generalizations and extensions provides deeper insight into the fundamental nature of distance and separation in various mathematical structures. For data practitioners, these concepts offer powerful tools for analyzing high-dimensional data, understanding the constraints of various distance metrics, and developing algorithms that efficiently navigate complex geometric spaces.

Examples and Problem-Solving

Understanding the triangle inequality becomes clearer through practical examples and problem-solving. Let's explore several scenarios that demonstrate how to apply this principle effectively.

Verifying triangle formation

Example 1: Determine whether sides of lengths 7, 10, and 16 can form a triangle.

Solution: We need to check all three triangle inequality conditions:

• 7 + 10 = 17 > 16 ✓
• 7 + 16 = 23 > 10 ✓
• 10 + 16 = 26 > 7 ✓

Since all three inequalities are satisfied, these measurements can form a triangle.

Example 2: Can sides of lengths 3, 4, and 8 form a triangle?

Solution: Let's check:

• 3 + 4 = 7 < 8 ✗
• 3 + 8 = 11 > 4 ✓
• 4 + 8 = 12 > 3 ✓

Since one of the conditions fails (the sum of the two shorter sides is less than the longest side), these measurements cannot form a triangle.

Using the triangle inequality in proofs

Example 3: Prove that ||x| - |y|| ≤ |x - y| for any real numbers x and y.

Solution: This is an application of the reverse triangle inequality. We start with the triangle inequality: |x| = |x - y + y| ≤ |x - y| + |y|

Rearranging: |x| - |y| ≤ |x - y|

Similarly, we can show that |y| - |x| ≤ |y - x| = |x - y|

Combined, these give us: -|x - y| ≤ |x| - |y| ≤ |x - y|

Therefore, ||x| - |y|| ≤ |x - y|, which is the reverse triangle inequality.

Applications in data science

Example 4: A clustering algorithm needs to determine if a point P is possibly within distance d of any point in a cluster C, without calculating the exact distance to every point in C. If we know the centroid of C and its radius r, how can the triangle inequality help?

Solution: Let's say the centroid of cluster C is point O with radius r (maximum distance from O to any point in C). For any point P outside the cluster:

• Let dist(P,O) be the distance from P to the centroid
• By the reverse triangle inequality, for any point Q in cluster C: dist(P,Q) ≥ dist(P,O) - dist(O,Q) dist(P,Q) ≥ dist(P,O) - r

If dist(P,O) - r > d, then dist(P,Q) > d for all points Q in cluster C, meaning P cannot be within distance d of any point in the cluster. This allows us to quickly eliminate entire clusters without computing individual distances.

Competitive mathematics

Example 5: In a mathematical olympiad problem: Given that |x - 3| + |x + 1| = 10, find the possible values of x.

Solution: This involves the triangle inequality in disguise. We can interpret it geometrically:

• |x - 3| represents the distance from x to 3 on the number line
• |x + 1| represents the distance from x to -1 on the number line
• Their sum equals 10

This means the point x on the number line is such that the sum of its distances to points 3 and -1 equals 10. The distance between points 3 and -1 is |3-(-1)| = 4.

When x is between -1 and 3, the sum of distances is simply (3-x) + (x+1) = 4, which doesn't equal 10.

When x ≤ -1, the sum is |x-3| + |x+1| = (3-x) + (-x-1) = 2-2x = 10, so x = -4.

When x ≥ 3, the sum is |x-3| + |x+1| = (x-3) + (x+1) = 2x-2 = 10, so x = 6.

Therefore, x = -4 or x = 6.

These examples demonstrate the triangle inequality's versatility across geometry, analysis, computational algorithms, and competitive mathematics. By mastering these applications, data practitioners can develop more efficient algorithms and gain deeper insights into the mathematical foundations of distance-based methods.

Conclusion

The triangle inequality is a mathematical principle with broad applications across many fields. What began as a simple observation about triangles has evolved into an important tool for distance calculations, optimization algorithms, and data analysis techniques.

To deepen your understanding of these concepts in data science, explore resources like the Machine Learning Scientist in Python career track. This program expands on mathematical concepts like the triangle inequality and helps develop the analytical skills needed for effective machine learning implementation.

The enduring relevance of the triangle inequality shows how elegant mathematical ideas continue to influence modern computational methods and algorithmic design across multiple disciplines.