Understanding Chebyshev Distance: A Comprehensive Guide

Data science and spatial analysis rely heavily on various distance metrics to solve complex problems. While Manhattan and Euclidean distances are widely recognized, another very interesting metric deserves attention: Chebyshev distance. This distance measure offers a distinct perspective on spatial relationships, particularly in grid-based environments and multidimensional data spaces.

In this guide, we'll explore the fundamentals of Chebyshev distance, examine its mathematical properties, and investigate its real-world applications. We'll also provide practical coding examples in Python and R, enabling you to implement Chebyshev distance calculations in your own projects. Also, if you are looking to deepen your understanding of how such metrics fit into broader data science workflows, our course on Designing Machine Learning Workflows in Python offers valuable insights into integrating various analytical techniques, including distance-based learning.

"Chessboard distance." Image by Dall-E.

What is Chebyshev Distance?

Chebyshev distance, named after the Russian mathematician Pafnuty Chebyshev, is defined as the maximum difference between the coordinates of two points along any single axis. Mathematically, for two points P = (x1, y1, ..., z1) and Q = (x2, y2, ..., z2) in n-dimensional space, the Chebyshev distance is expressed as:

This definition sets Chebyshev distance apart from other common metrics like Manhattan distance (which sums the absolute differences) and Euclidean distance (which calculates the straight-line distance). 

How Chebyshev Distance Works

Let’s look at how Chebyshev distance works in order to build our intuition. 

Geometric interpretation 

Chebyshev distance emphasizes the maximum shift in any coordinate direction, which is pivotal in scenarios where movement is not restricted to horizontal or vertical paths but includes any direct line.

Consider two points in a 2-dimensional space: Point A at coordinates (1, 1) and Point B at coordinates (4, 5). To find the Chebyshev distance between these two points, we focus on the maximum difference along any one coordinate axis.

• The difference along the x-axis: |4 - 1| = 3
• The difference along the y-axis: |5 - 1| = 4

Here, the Chebyshev distance is 4 because Chebyshev distance = max(3, 4) = 4.

The accompanying visual illustrates these points on a grid, highlighting the area that falls within a Chebyshev distance of 4 from Point A. The yellow shaded area shows all the positions that are reachable within this distance metric. 

Chebyshev Distance Demonstrated in a 2D Coordinate System. Image by Author. 

Grid interpretation

Chebyshev distance is also commonly called chessboard distance because it can be easily understood in the context of chess: The Chebyshev distance between two squares is equivalent to the number of king moves required to go from one square to the other. This interpretation can be visualized on our grid, where each number represents the Chebyshev distance from the central square (where the king is located) to every other square on the board.

Chebyshev Distance Visualized on a Chessboard Layout. Image by Author. 

In our visual model, the king is positioned on c5. The numbers on the chessboard represent the Chebyshev distance from c5 to all other squares. For example, the distance from c5 to e7 is 2 because the king can reach e7 in two moves: one diagonal move to d6, followed by another diagonal move to e7. Similarly, the distance to the nearest edge squares (like c8 or h5) is simply counted by the number of direct horizontal or vertical moves.

This grid-based approach to explaining Chebyshev distance highlights its practical application in games like chess and is also relevant in pathfinding algorithms used in robotics and artificial intelligence, where the goal is to find the most efficient path between points in a grid.

Applications of Chebyshev Distance

The properties of Chebyshev distance make it valuable in various fields, particularly where grid-like structures or simultaneous movement along different axes are involved. Let's explore some applications:

Robotics and warehouse logistics

In environments where robots or automated systems move along grid patterns, Chebyshev distance can optimize path planning. Imagine, for example, agricultural robots navigating crop fields or autonomous vehicles in structured environments. 

In automated warehouses, robots often move along grid-like paths. Chebyshev distance helps optimize their movements, especially when they can move diagonally. This optimization can significantly improve efficiency in item retrieval and storage processes.

Image processing

In digital image analysis, Chebyshev distance is used in pixel-based operations. It helps define neighborhoods around a pixel for various transformations and filters. This is often used in tasks like edge detection or pattern recognition.

The ability to consider diagonal pixels as easily as horizontal or vertical ones makes Chebyshev distance particularly useful in these applications.

Geographic information systems (GIS)

Urban planners and emergency services can use Chebyshev distance to calculate the minimum number of moves required between two points on a grid map. This is valuable for optimizing emergency route planning in cities with grid-like street layouts or planning efficient public transportation routes.

In these scenarios, Chebyshev distance can provide a quick estimate of travel time or distance in environments where diagonal movement is possible.

Machine learning and data science

In the field of machine learning and data science, Chebyshev distance finds applications in certain clustering algorithms or anomaly detection systems.

It's particularly useful in scenarios where the maximum difference along any dimension is more important than the overall difference. For example, in anomaly detection, a data point that significantly deviates in just one feature might be considered an anomaly, regardless of its values in other dimensions.

Game development

Beyond chess, Chebyshev distance has broader applications in game development, especially for grid-based games. It can model movement costs for entities that can move diagonally as easily as horizontally or vertically. This is particularly useful in strategy games, roguelikes, or any game with grid-based movement. 

Also, by incorporating Chebyshev distance, game developers can create more detailed and realistic movement mechanics, enhancing gameplay and strategic depth.

Mathematical Properties of Chebyshev Distance

Chebyshev distance satisfies all the properties of a metric space, which is crucial for its application in various fields. Let's verify these properties:

1. Non-negativity: For any two points x and y, d(x, y) ≥ 0
   The Chebyshev distance is always non-negative because it's defined as the maximum of absolute differences, which are always non-negative.

2. Identity of indiscernibles: d(x, y) = 0 if and only if x = y
   The Chebyshev distance between a point and itself is always 0. If the Chebyshev distance is 0, it means the maximum difference along any dimension is 0, implying the points are identical.

3. Symmetry: d(x, y) = d(y, x)
   The order of points doesn't matter in Chebyshev distance calculation. The maximum absolute difference remains the same regardless of which point is considered first.

4. Triangle inequality: d(x, z) ≤ d(x, y) + d(y, z)
   This property holds for Chebyshev distance. Intuitively, the maximum difference between x and z along any dimension cannot be greater than the sum of the maximum differences from x to y and from y to z.

These properties ensure that Chebyshev distance behaves consistently and intuitively in various mathematical and practical applications.

Comparing Chebyshev with Other Distance Metrics

In the visual below, we explore the differences between Manhattan, Euclidean, and Chebyshev distances: 

Comparison of Chebyshev, Manhattan, and Euclidean Distances. Image by Author. 

• Manhattan Distance (D=7): Illustrated by the magenta dashed line, this metric sums the absolute differences of their Cartesian coordinates. It is often visualized as a path traveling along grid lines in a rectilinear pattern, reflecting its real-world analogy to city block distances where one can only travel along orthogonal streets. For a deeper understanding of this metric you can refer to our comprehensive tutorial, What is Manhattan Distance? 
• Euclidean Distance (D=5): Shown by the green solid line, this is the "straight-line" distance between two points in Euclidean space. It is the most intuitive form of distance: the direct path connecting two points.
• Chebyshev Distance (D=4): Represented by the yellow shaded area, this distance metric is defined as the maximum of the absolute differences between the coordinates of a pair of objects. It is particularly useful in scenarios where you can move in any direction from a grid point with diagonal moves allowed.

Relation to Minkowski distance

Chebyshev distance is closely related to a broader family of distance metrics known as Minkowski distances. In fact, Chebyshev distance is a special case of the Minkowski distance.

The Minkowski distance of order p between two points x = (x₁, ..., xn) and y = (y₁, ..., yn) is defined as:

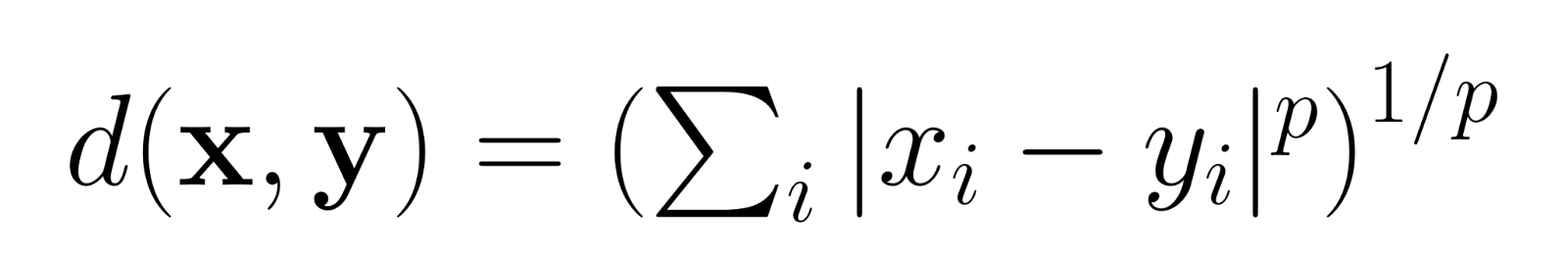
Where:

• p ≥ 1 is a real number
• n is the number of dimensions

The Chebyshev distance emerges as a special case when p approaches infinity. Mathematically, we can express this as:

This relationship places Chebyshev distance in context with other well-known distance metrics:

• When p = 1, we get Manhattan distance.
• When p = 2, we get Euclidean distance.
• When p → ∞, we get Chebyshev distance.

Understanding this relationship helps in choosing the appropriate distance metric for specific applications, as each metric emphasizes different aspects of the distance between points.

Chebyshev Distance in Python and R

To help you implement Chebyshev distance calculations in your projects, let's look at how to do this in two popular programming languages: Python and R. These examples will demonstrate how to calculate the Chebyshev distance between two points in 2D space.

Python example

Python offers a straightforward way to calculate Chebyshev distance using the SciPy library. Here's how you can do it:

from scipy.spatial import distance

# Define points
point_A = (1, 1)
point_B = (4, 5)

# Calculate Chebyshev distance
chebyshev_dist = distance.chebyshev(point_A, point_B)

print(f"The Chebyshev distance between {point_A} and {point_B} is {chebyshev_dist}.")

The Chebyshev distance between (1, 1) and (4, 5) is 4.

In this Python example, we use the distance.chebyshev() function from SciPy's spatial module. This function takes two points as arguments and returns their Chebyshev distance. The points are represented as tuples, making it easy to work with coordinates in any dimension.

R example

For R users, we can calculate Chebyshev distance using the philentropy package. Here's how to do it:

# Install and Load the philentropy package
# install.packages("philentropy")
library(philentropy)

# Define points
point_A <- c(1, 1)
point_B <- c(4, 5)

# Bind points into a matrix
points_matrix <- rbind(point_A, point_B)

# Calculate Chebyshev distance
chebyshev_dist <- distance(points_matrix, method = "chebyshev")

# Print the result
print(paste("The Chebyshev distance between points is:", chebyshev_dist))

The Chebyshev distance between points is: 4

In this R example, we first load the philentropy package. We define our points as vectors and then stack them to make a matrix. The distance() function from philentropy is then used to calculate the Chebyshev distance; we just have to specify chebyshev in the method argument.

These code snippets provide a practical starting point for implementing Chebyshev distance calculations in your data science or machine learning projects.

Conclusion

Throughout this article, we've explored Chebyshev distance and its valuable perspective on measuring spatial relationships. Its ability to capture the maximum difference along any dimension makes it particularly suited for scenarios where movement in any direction is equally easy or costly, such as in robotics, warehouse logistics, and chess algorithms.

As you continue to explore spatial metrics and data analysis, remember that Chebyshev distance offers a distinct lens through which to view and solve complex spatial problems. Consider exploring our Machine Learning in Production skill track to help you bridge the gap between theoretical understanding and practical implementation of machine learning models, including the application of distance metrics in production environments. For those looking to validate their expertise in these areas, the Data Scientist Certification provides a recognized credential that demonstrates proficiency in essential data science skills, including the use of different distance metrics and their applications.