Track
Disclaimer: This tutorial is not political in nature—it only uses the upcoming U.S. presidential election as a way to write educational content on machine learning. Opinions are mine and don't represent DataCamp's views.
After successfully predicting the results of EURO 2024 using machine learning, I’ve shifted my focus to an even more high-stakes event: the 2024 U.S. presidential election.
With the race expected to be a tight contest between Vice President Kamala Harris and Former President Donald Trump, let’s use machine learning to predict who will win!
I wrote this blog for a technical audience familiar with Python and machine learning. If you’re only looking for the prediction result, jump to the final section titled “US Election 2024 Prediction.”
If you’d like to try out the code I used, I’ve made it all available in this DataLab notebook.
Become an ML Scientist
Data Sources: FiveThirtyEight and Federal Election Commission
The data used for our prediction is from FiveThirtyEight, which gathers poll data from all kinds of different pollsters. The data is available via their GitHub for all election cycles since 1968.
We will use their poll model, which assigns the average poll percentage for each candidate in each state for (almost) each given date in the eight months leading up to the election.
We start with importing 2024, 2020, and historical polling data from CSV files. The 2024 data is filtered on polls from the current cycle only, and the historical data until 2016 is concatenated with the 2020 data. In the resulting two DataFrames, polls_24 and polls_until_20, the date columns are converted into a datetime format to ensure consistency, and relevant columns like cycle, state, candidate name, and polling estimates are kept.
import pandas as pd
# Reading CSV files
polls_24 = pd.read_csv('presidential_general_averages.csv')
polls_20 = pd.read_csv('presidential_poll_averages_2020.csv')
polls_until_16 = pd.read_csv('pres_pollaverages_1968-2016.csv')
# Filtering and concatenating DataFrames
polls_24 = polls_24[polls_24['cycle'] == 2024]
polls_until_20 = pd.concat([polls_20, polls_until_16], ignore_index=True)
# Making sure dates are in datetime format
polls_24['date'] = pd.to_datetime(polls_24['date'], format='%Y-%m-%d')
polls_until_20['modeldate'] = pd.to_datetime(polls_until_20['modeldate'])
# Keeping only the columns of interest
polls_until_20 = polls_until_20[['cycle', 'state', 'modeldate', 'candidate_name', 'pct_estimate', 'pct_trend_adjusted']]For the actual voting results by state, I took the data straight from the Federal Election Commission of the USA. For simplicity’s sake, I summarized them into one CSV file beforehand.
One observation represents the combination of election cycle, state and party, each completed with the name of the respective candidate and, of course, the vote share percentage this candidate achieved.
# Importing result data
results_until_20 = pd.read_csv('results.csv', sep=';')
results_until_20 = results_until_20[['cycle', 'state', 'party', 'candidate', 'vote_share']]To ensure we're working with relevant and high-quality data, I’ve applied two key restrictions:
- I’ll focus on the last six election cycles (2000 and onward) as data availability and accuracy improved significantly during this period.
- I’ll narrow down the analysis to swing states—those with the closest races—based on states where the leading candidate had less than a five percent advantage, according to FiveThirtyEight’s election forecast. The selected swing states are Pennsylvania, Wisconsin, Michigan, Georgia, North Carolina, Arizona, and Nevada. We assume the other states will vote as expected, define the lists
swing_states,blue_statesandred_statesaccordingly, and create subsets of the data for the swing states.
# Implementing cycle restriction
start_cycle = 2000
polls_until_20 = polls_until_20[polls_until_20['cycle'] >= start_cycle]
# Defining state lists
swing_states = [
'Pennsylvania', 'Wisconsin', 'Michigan', 'Georgia',
'North Carolina', 'Arizona', 'Nevada'
]
blue_states = [
'District of Columbia', 'Vermont', 'Massachusetts', 'Maryland',
'Hawaii', 'California', 'ME-1', 'Connecticut', 'Washington',
'Delaware', 'Rhode Island', 'New York', 'Illinois', 'New Jersey',
'Oregon', 'Colorado', 'Maine', 'New Mexico', 'Virginia',
'New Hampshire', 'NE-2', 'Minnesota'
]
red_states = [
'Wyoming', 'West Virginia', 'Oklahoma', 'North Dakota',
'Idaho', 'South Dakota', 'Arkansas', 'Kentucky', 'NE-3',
'Alabama', 'Tennessee', 'Utah', 'Louisiana', 'Nebraska',
'Mississippi', 'Montana', 'NE-1', 'Indiana', 'Kansas',
'Missouri', 'South Carolina', 'Alaska', 'Ohio', 'Iowa',
'Texas', 'ME-2', 'Florida'
]
# Defining swing state subset of the poll data
swing_until_20 = polls_until_20[polls_until_20['state'].isin(swing_states)]
swing_24 = polls_24[polls_24['state'].isin(swing_states)]Exploratory Data Analysis and Data Cleaning
To get an overview of our data, we perform some exploratory data analysis (EDA). First, we use a combination of the .isnull() and .sum() methods to see which columns each DataFrame includes and where data might be missing.
# Checking for missing values in swing_24 and swing_until_20
print(swing_24.isnull().sum())
print(swing_until_20.isnull().sum())candidate 0
date 0
pct_trend_adjusted 4394
state 0
cycle 0
party 0
pct_estimate 0
hi 0
lo 0
dtype: int64
cycle 0
state 0
modeldate 0
candidate_name 0
pct_estimate 0
pct_trend_adjusted 0
dtype: int64As we can see, the column names differ between the two DataFrames, and the party column seems to be missing in swing_until_20. Moreover, there seem to be two different kinds of percentages measured: an estimated percentage and one that was additionally trend-adjusted. However, the trend-adjusted percentage seems not to be available for the 2024 data. We will investigate this later.
Let’s check for the distinct values of each of our categorical variables next:
print('2024 data:')
print(swing_24['date'].min()) # earliest polling date
print(swing_24['date'].max()) # latest polling date
print(swing_24['state'].unique().tolist()) # distinct states
print(swing_24['party'].unique().tolist()) # distinct parties
print(swing_24['candidate'].unique().tolist()) # distinct candidates
print('Historical data:')
print(swing_until_20['modeldate'].min())
print(swing_until_20['modeldate'].max())
print(swing_until_20['state'].unique().tolist())
print(swing_until_20['candidate_name'].unique().tolist())2024 data:
2024-03-01 00:00:00
2024-10-29 00:00:00
['Arizona', 'Georgia', 'Michigan', 'Nevada', 'North Carolina', 'Pennsylvania', 'Wisconsin']
['REP', 'DEM', 'IND']
['Trump', 'Harris', 'Kennedy', 'Biden']
Historical data:
2000-03-02 00:00:00
2020-11-03 00:00:00
['Wisconsin', 'Pennsylvania', 'North Carolina', 'Nevada', 'Michigan', 'Georgia', 'Arizona']
['Joseph R. Biden Jr.', 'Donald Trump', 'Convention Bounce for Joseph R. Biden Jr.', 'Convention Bounce for Donald Trump', 'Hillary Rodham Clinton', 'Gary Johnson', 'Barack Obama', 'Mitt Romney', 'John McCain', 'George W. Bush', 'John Kerry', 'Al Gore', 'Ralph Nader']While the data looks good for states and dates, there are some things to notice about the candidate-related columns. The historical data (that of the cycle 2020 more specifically) includes not only percentages of the two candidates but also convention bounces, i.e. increases in support after holding their national convention. Furthermore, the first names seem to be missing in swing_24.
For our investigation of the different kinds of percentages, it is crucial to remove the convention bounce observations immediately:
# Only keep rows where candidate_name does not start with 'Convention Bounce'
swing_until_20 = swing_until_20[~swing_until_20['candidate_name'].str.startswith('Convention Bounce')]Estimated vs. trend-adjusted percentage
To ensure consistency, the kind of percentage has to be the same for all training and testing data. As we have discovered, only the data up to the 2020 election cycle contains both estimated and trend-adjusted percentages, while there are only the estimated ones for 2024. That leaves us with two options, which are:
- Using the estimated percentage for all cycles
- Calculating our own trend-adjusted percentage for 2024
The way in which the trend-adjusted percentage was calculated for the historical data is unclear. That’s why we have to investigate the relationship between the estimated and trend-adjusted percentages before moving on to data cleaning, as the choice of the data basis is crucial for our predictions. First, we investigate the correlation and average difference in the historical data.
# Checking the correlation between the percentages
adj_corr_swing = swing_until_20['pct_estimate'].corr(swing_until_20['pct_trend_adjusted'])
print('Correlation between estimated and trend-adjusted percentage in swing states: ' + str(adj_corr_swing))
# Calculate the mean difference between pct_estimate and pct_trend_adjusted, grouping by date, state, and party
mean_diff = (swing_until_20['pct_estimate'] - swing_until_20['pct_trend_adjusted']).mean()
print('Mean difference between estimated and trend-adjusted percentage in swing states: ' + str(mean_diff))Correlation between estimated and trend-adjusted percentage in swing states: 0.9953626583357665
Mean difference between estimated and trend-adjusted percentage in swing states: 0.24980898513865013We can see that the correlation between both is extremely high (99,5%), as one could expect. The average difference of about 0.25 percent points looks small at first, but it might make a difference in very close races, like those expected in Nevada or Michigan.
Since all electoral votes in each state go to the winner, the order between the candidates is more important than any precise percentage. What we want to avoid is a discrepancy close to the election date. Therefore, we can look at the number of observations in which the leading candidate between the two percentages differed in the last election cycle of 2020 and the last date of such an occurrence.
# Finding out how often pct_estimate and pct_trend_adjusted saw different candidates in the lead in the 2020 race
swing_20 = swing_until_20[swing_until_20['cycle'] == 2020]
# Create a new column to indicate if the ranking is different between pct_estimate and pct_trend_adjusted
swing_20['rank_estimate'] = swing_20.groupby(['state', 'modeldate'])['pct_estimate'].rank(ascending=False)
swing_20['rank_trend_adjusted'] = swing_20.groupby(['state', 'modeldate'])['pct_trend_adjusted'].rank(ascending=False)
# Rows where the rankings are different in swing states
different_rankings_swing = swing_20[swing_20['rank_estimate'] != swing_20['rank_trend_adjusted']]
print('Number of observations with differing leader: ' + str(different_rankings_swing.shape[0] / 2))
print('Last occurrence: ' + str(different_rankings_swing['modeldate'].max()))Number of observations with differing leader: 34.0
Last occurrence: 2020-06-24 00:00:00Apparently, the lead differed only in 34 cases, so about 5 days per swing state on average. As the last occurrence is at the end of June, all instances appear to be in the early phase of the election campaign.
Considering all that, the rare instances of leadership change are unlikely to sway the model's overall accuracy, especially with us having a sizable dataset spanning multiple cycles. Therefore, I chose the first option and only used the estimated percentage throughout all election cycles. This ensures data consistency, which is key in machine learning to prevent the model from learning biases introduced by differing data processing methods.
Adding party column and historical result data
To add a column for the political party, we first get a list of all candidates in the historical dataset. Then, we create a dictionary with candidates as keys and the respective party as corresponding value—ChatGPT is great for this to save research time! Finally, we combine both in a DataFrame, and merge it to swing_until_20.
# Get unique candidate names
candidate_names = swing_until_20['candidate_name'].unique().tolist()
# Create a dictionary of candidates and their political party
party_map = {
'Joseph R. Biden Jr.': 'DEM',
'Donald Trump': 'REP',
'Hillary Rodham Clinton': 'DEM',
'Gary Johnson': 'LIB',
'Barack Obama': 'DEM',
'Mitt Romney': 'REP',
'John McCain': 'REP',
'Ralph Nader': 'IND',
'George W. Bush': 'REP',
'John Kerry': 'DEM',
'Al Gore': 'DEM'
}
# Create a DataFrame with candidates and their respective parties
candidate_df = pd.DataFrame(candidate_names, columns=['candidate_name'])
candidate_df['party'] = candidate_df['candidate_name'].map(party_map)
# Merge the candidate_df with swing_until_20 on 'candidate' column
swing_until_20 = swing_until_20.merge(candidate_df[['candidate_name', 'party']], on='candidate_name', how='left')Now that we have added the party column to our swing_until_20 DataFrame, we can merge the historical election results to it in a new column called vote_share. Since the CSV file of the vote_share was in a different format, we need to adjust it to the same one used in the pct_estimate column.
# Merging results_until_20 to swing_until_20
swing_until_20 = pd.merge(swing_until_20, results_until_20, how='left', left_on=['cycle', 'state', 'party', 'candidate_name'], right_on=['cycle', 'state', 'party', 'candidate'])
swing_until_20['vote_share'] = swing_until_20['vote_share'].str.replace(',', '.')
swing_until_20['vote_share'] = pd.to_numeric(swing_until_20['vote_share'])Aligning columns and column names
Finally, we rename the modeldate column to date, remove all unnecessary columns, and adjust the candidate format in the 2024 data to also include first names.
# Renaming columns in swing_until_20
swing_until_20.rename(columns={'modeldate': 'date'}, inplace=True)
# Keeping only relevant columns
swing_24 = swing_24[['cycle', 'date', 'state', 'party', 'candidate', 'pct_estimate']]
swing_until_20 = swing_until_20[['cycle', 'date', 'state', 'party', 'candidate', 'pct_estimate', 'vote_share']]
# Update candidate names in swing_24 dataframe
swing_24['candidate'] = swing_24['candidate'].replace({
'Trump': 'Donald Trump',
'Biden': 'Joseph R. Biden Jr.',
'Harris': 'Kamala Harris',
'Kennedy': 'Robert F. Kennedy'})Overview of the 2024 campaign
Let’s get some overview over the course of the 2024 election campaign so far. We use seaborn and matplotlib to create a line chart showing the average polling progression across all selected swing states. The red, blue, and black lines show the polling percentages of Republicans, Democrats, and independent candidates. Vertical lines mark significant events during the campaign.
import matplotlib.pyplot as plt
import seaborn as sns
# Ensure the date column is in datetime format
swing_24['date'] = pd.to_datetime(swing_24['date'])
# Group by date and party, then average the pct_estimate
swing_24_grouped = swing_24.groupby(['date', 'party'])['pct_estimate'].mean().reset_index()
# Create the line chart
plt.figure(figsize=(14, 8))
sns.lineplot(data=swing_24_grouped, x='date', y='pct_estimate', hue='party', marker='o',
palette={'REP': 'red', 'DEM': 'blue', 'IND': 'black'})
# Add vertical lines for significant events
plt.axvline(pd.to_datetime('2024-07-13'), color='red', linestyle='--', alpha=0.25)
plt.axvline(pd.to_datetime('2024-08-05'), color='blue', linestyle='--', alpha=0.25)
plt.axvline(pd.to_datetime('2024-07-23'), color='blue', linestyle='--', alpha=0.25)
plt.axvline(pd.to_datetime('2024-09-05'), color='black', linestyle='--', alpha=0.25)
plt.axvline(pd.to_datetime('2024-10-01'), color='black', linestyle='--', alpha=0.25)
# Add text annotations for significant events
plt.text(pd.to_datetime('2024-07-13'), plt.ylim()[1] * 0.6, 'Trump Assassination Attempt', color='red', ha='right')
plt.text(pd.to_datetime('2024-07-23'), plt.ylim()[1] * 0.5, 'First Harris Rally', color='blue', ha='right')
plt.text(pd.to_datetime('2024-08-05'), plt.ylim()[1] * 0.4, 'Official Nomination of Harris', color='blue', ha='right')
plt.text(pd.to_datetime('2024-09-05'), plt.ylim()[1] * 0.3, 'Presidential Debate', color='black', ha='right')
plt.text(pd.to_datetime('2024-10-01'), plt.ylim()[1] * 0.2, 'Vice Presidential Debate', color='black', ha='right')
# Add horizontal gridlines at values divisible by 5
plt.yticks(range(0, 51, 5))
plt.grid(axis='y', linestyle='--', alpha=0.7)
# Limit the y-axis range to 50
plt.ylim(0, 50)
# Adjust the legend
plt.legend(title='Party')
# Set titles and labels
plt.title('Average Polling Percentage per Party Over Time in Swing States')
plt.xlabel('Date')
plt.ylabel('Average Polling Percentage')
plt.show()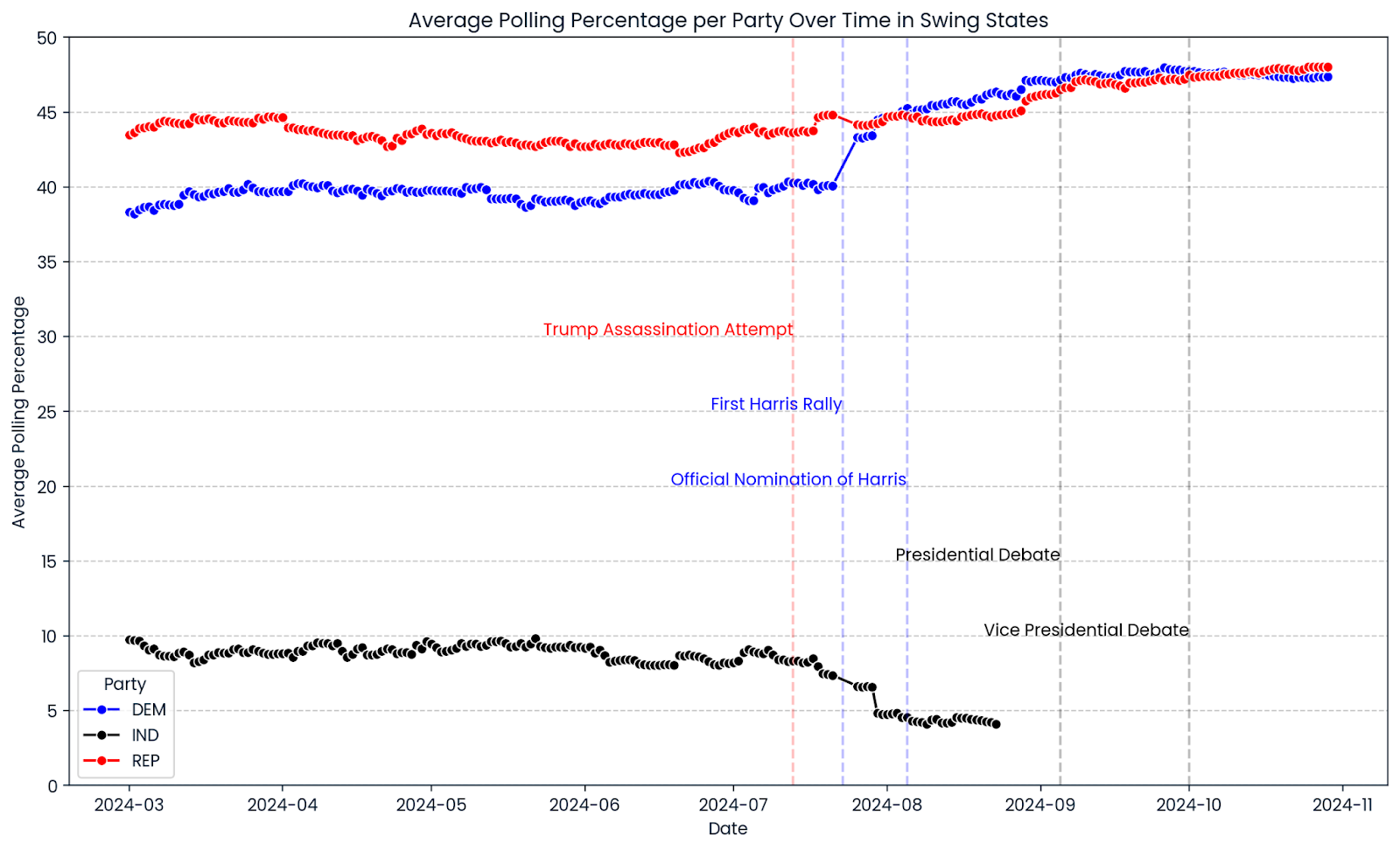
A first glimpse into the progression of 2024 polling shows a very narrow across the swing states. The approval rate of Donald Trump was relatively constant throughout the campaign with a recent slight uptick. The Democratic Party’s percentage kept up after Kamala Harris was officially nominated as their presidential candidate on August 5th, 2024, significantly exceeding the polls of former candidate and President of the United States, Joe Biden. Either way, the graphs show a picture of many races way too close to call.
Become a Data Engineer
Feature Engineering for Predicting the 2024 US Elections
We will explore four categories of features: opponent-related, time-related, candidate-related, and party-related.
Opponent-related features
One interesting feature of this year’s election campaign is the role of Robert F. Kennedy, whose polling percentages suggest a support that is unusually high for an independent candidate. He suspended his campaign on August 23rd, 2024, leading to an increase in the approval of both Kamala Harris and Donald Trump.
Because we want to prevent our models from learning the wrong things and predict vote shares that add up to more than 100%, we include the third-party percentage as a feature.
# Adding the percentage of 3rd party candidates
swing_24['pct_3rd_party'] = swing_24.groupby(['cycle', 'date', 'state'])['pct_estimate'].transform(
lambda x: x[~swing_24['party'].isin(['DEM', 'REP'])].sum()
)
swing_until_20['pct_3rd_party'] = swing_until_20.groupby(['cycle', 'date', 'state'])['pct_estimate'].transform(
lambda x: x[~swing_until_20['party'].isin(['DEM', 'REP'])].sum()
)Now that we have included third-party support in our features, we can pay tribute to the fact that, realistically speaking, there are only two parties whose candidates have a winning chance. Accordingly, we remove all candidates from parties other than the Democratic and Republican Party in both DataFrames.
# Removing observations of candidates who are not Democrats and Republicans
swing_24 = swing_24[swing_24['party'].isin(['DEM', 'REP'])]
swing_until_20 = swing_until_20[swing_until_20['party'].isin(['DEM', 'REP'])]Two more pieces of information that interest us are the percentage of the opponent on any given date in a given state, as well as the lead (or lag) of approval compared to the opponent. We add both features using lambda functions.
# Adding the percentage of the opponent
swing_24['pct_opponent'] = swing_24.apply(
lambda row: swing_24[
(swing_24['date'] == row['date']) &
(swing_24['state'] == row['state']) &
(swing_24['party'] != row['party'])
]['pct_estimate'].sum(),
axis=1
)
swing_until_20['pct_opponent'] = swing_until_20.apply(
lambda row: swing_until_20[
(swing_until_20['date'] == row['date']) &
(swing_until_20['state'] == row['state']) &
(swing_until_20['party'] != row['party'])
]['pct_estimate'].sum(),
axis=1
)
# Adding the lead against the opponent
swing_24['lead'] = swing_24['pct_estimate'] - swing_24['pct_opponent']
swing_until_20['lead'] = swing_until_20['pct_estimate'] - swing_until_20['pct_opponent']Time-related features
In the feature engineering process, I chose to incorporate the days until the election, a rolling average of poll percentages grouped by party, and momentum indicators grouped by candidate. This approach allows us to capture both the stable trends in party support and the rapid shifts in individual candidate popularity.
# Days until election
election_dates = {
2000: pd.to_datetime('2000-11-07'),
2004: pd.to_datetime('2004-11-02'),
2008: pd.to_datetime('2008-11-04'),
2012: pd.to_datetime('2012-11-06'),
2016: pd.to_datetime('2016-11-08'),
2020: pd.to_datetime('2020-11-03')
}
swing_until_20['election_date'] = swing_until_20['cycle'].map(election_dates)
swing_24['election_date'] = pd.to_datetime('2024-11-05')
swing_24['days_until_election'] = (swing_24['election_date'] - swing_24['date']).dt.days
swing_until_20['days_until_election'] = (swing_until_20['election_date'] - swing_until_20['date']).dt.days
# Party 7 days rolling average
swing_24 = swing_24.sort_values(by='date')
swing_24['rolling_avg_7d'] = swing_24.groupby(['state', 'party'])['pct_estimate'].transform(
lambda x: x.rolling(window=7, min_periods=1).mean()
)
swing_until_20 = swing_until_20.sort_values(by='date')
swing_until_20['rolling_avg_7d'] = swing_until_20.groupby(['cycle', 'state', 'party'])['pct_estimate'].transform(
lambda x: x.rolling(window=7, min_periods=1).mean()
)Using the days until the election as a feature enables us to directly model the effect of time on voter preferences, acknowledging that polls conducted closer to Election Day often hold greater predictive value due to heightened voter engagement and more settled opinions. By grouping the rolling average by party, we smooth out short-term fluctuations and emphasize the underlying trends in party affiliation, providing a stable and reliable metric of overall party support.
Meanwhile, grouping the momentum indicator by candidate captures the rapid changes in candidate approval, reflecting how individual candidates can gain or lose support swiftly due to factors like campaign events or news coverage. This distinction is particularly pertinent given the mid-campaign nominee change in the Democratic Party, which substantially impacts polling dynamics. We are especially interested in the difference between both candidates’ momentum.
# Calculate the daily change (momentum) for each candidate
swing_24['momentum_candidate'] = swing_24.groupby(['state', 'party'])['pct_estimate'].diff()
swing_until_20['momentum_candidate'] = swing_until_20.groupby(['state', 'party'])['pct_estimate'].diff()
# Calculate the daily change (momentum) for each opponent
swing_24['momentum_opponent'] = swing_24.groupby(['state', 'party'])['pct_opponent'].diff()
swing_until_20['momentum_opponent'] = swing_until_20.groupby(['state', 'party'])['pct_opponent'].diff()
# Calculate the difference between the candidate's momentum and the opponent's momentum
swing_24['momentum'] = swing_24['momentum_candidate'] - swing_24['momentum_opponent']
swing_until_20['momentum'] = swing_until_20['momentum_candidate'] - swing_until_20['momentum_opponent']Candidate-related features
Candidate-wise, we first create two binary features about whether or not a candidate is the incumbent President or incumbent Vice President. This way, we enable our models to account for the effects of the candidate's presidential track record.
We do this by applying a lambda function to both DataFrames, which compares the candidate name and election cycle to the dictionaries incumbent_presidents and incumbent_vice_presidents that we create for this purpose.
incumbent_presidents = {
2000: 'Bill Clinton',
2004: 'George W. Bush',
2008: 'George W. Bush',
2012: 'Barack Obama',
2016: 'Barack Obama',
2020: 'Donald Trump',
2024: 'Joseph R. Biden Jr.'
}
incumbent_vice_presidents = {
2000: 'Al Gore',
2004: 'Richard Cheney',
2008: 'Richard Cheney',
2012: 'Joseph R. Biden Jr.',
2016: 'Joseph R. Biden Jr.',
2020: 'Mike Pence',
2024: 'Kamala Harris'
}
# Adding is_incumbent_president column
swing_until_20['is_incumbent_president'] = swing_until_20.apply(
lambda row: row['candidate'] == incumbent_presidents.get(row['cycle'], ''), axis=1
)
swing_24['is_incumbent_president'] = swing_24.apply(
lambda row: row['candidate'] == incumbent_presidents.get(row['cycle'], ''), axis=1
)
# Adding is_incumbent_vice_president column
swing_until_20['is_incumbent_vice_president'] = swing_until_20.apply(
lambda row: row['candidate'] == incumbent_vice_presidents.get(row['cycle'], ''), axis=1
)
swing_24['is_incumbent_vice_president'] = swing_24.apply(
lambda row: row['candidate'] == incumbent_vice_presidents.get(row['cycle'], ''), axis=1
)Methodologically, it does not make sense to use a dummy feature for any candidate who is or was not running in 2024 or who is a first-time nominee time in 2024. We will, therefore, only create such features for Donald Trump and Biden since there is data for both of them from the 2016 and 2020 elections, respectively.
# Create a feature for candidates from 2024 who were candidates in earlier cycles
swing_24['candidate_Donald Trump'] = swing_24['candidate'] == 'Donald Trump'
swing_until_20['candidate_Donald Trump'] = swing_until_20['candidate'] == 'Donald Trump'
swing_24['candidate_Joseph R. Biden Jr.'] = swing_24['candidate'] == 'Joseph R. Biden Jr.'
swing_until_20['candidate_Joseph R. Biden Jr.'] = swing_until_20['candidate'] == 'Joseph R. Biden Jr.'Party-related features
Similar to the candidate incumbency, we include a feature for party incumbency. It might enhance our models’ ability to accurately predict vote shares by recognizing the historical trends and voter sentiments linked to the party currently holding office.
# Define incumbent party for each election
incumbent_party = {
2000: 'DEM',
2004: 'REP',
2008: 'REP',
2012: 'DEM',
2016: 'DEM',
2020: 'REP',
2024: 'DEM'
}
# Define is_incumbent_party
swing_until_20['is_incumbent_party'] = swing_until_20.apply(
lambda row: row['party'] == incumbent_party.get(row['cycle'], ''), axis=1
)
swing_24['is_incumbent_party'] = swing_24.apply(
lambda row: row['party'] == incumbent_party.get(row['cycle'], ''), axis=1
)Regarding the party itself, there are two options on how to consider them: we could either create one model per state and party, or one model per state and one-hot encode the party into two features party_DEM and party_REP.
The latter option offers several advantages over building separate models for each state and party. It uses more data for training, improves model robustness, simplifies the development process, and provides flexibility to capture both shared and party-specific patterns in the data.
# Create duplicate party column for one-hot encoding
swing_24['party_dummy'] = swing_24['party']
swing_until_20['party_dummy'] = swing_until_20['party']
# One-hot encode the duplicate party column in swing_24 and swing_until_20
swing_24 = pd.get_dummies(swing_24, columns=['party_dummy'], prefix='party')
swing_until_20 = pd.get_dummies(swing_until_20, columns=['party_dummy'], prefix='party')One thing we have to keep in mind is that we need the party column in the original format to group the prediction results. That is why we duplicated it and performed one-hot encoding on the duplicate column.
Of course, there would be quite many other possible features to include. For instance, we could use demographic or economic indicators for each of the states, but expanding the feature set further with different datasets would go beyond the scope of this article.
AI Upskilling for Beginners
Final Preparations for our Machine Learning Models
In this section, we'll ensure our data is clean and ready for our machine learning models, focusing on handling missing values and understanding the distributions of our key variables.
Checking for missing values
There are a few things left to verify that the data is in the right structure for the models to be trained on. First, we investigate whether any columns in both datasets have missing values.
# Calculate the number of missing values in each column of swing_until_20
missing_values_until_20 = swing_until_20.isnull().sum()
missing_values_24 = swing_24.isnull().sum()
# Filter out columns that have no missing values
missing_values_until_20 = missing_values_until_20[missing_values_until_20 > 0]
missing_values_24 = missing_values_24[missing_values_24 > 0]
# Display the columns with at least 1 missing value and their respective counts for both dataframes
print(missing_values_until_20, missing_values_24)momentum 84 dtype: int64
momentum 21 dtype: int64The candidate momentum is the only column with missing values. This makes sense since it is calculated as the daily difference between poll values for each candidate, so we’d expect their first observation to be without the momentum column. We can simply remove the missing values.
# Dropping missing values
swing_24 = swing_24.dropna()
swing_until_20 = swing_until_20.dropna()Analyzing distributions
Taking a look at the distributions of the numeric columns will give us a picture of whether we have some hidden outliers or whether the data is plausible overall.
Moreover, we can compare the 2024 election cycle polling to the average of the former cycles. We can leave out some of the features like pct_opponent and rolling_avg_7d since they basically result from the pct_estimate column and will resemble basically the same distribution.
# Getting description of distributions in both DataFrames
swing_until_20[['pct_estimate', 'lead', 'pct_3rd_party', 'momentum', 'vote_share']].describe()
print(swing_24[['pct_estimate', 'lead', 'pct_3rd_party','momentum']].describe())|
pct_estimate |
lead |
pct_3rd_party |
momentum |
vote_share |
|
|
count |
20504 |
20504 |
20504 |
20504 |
20504 |
|
mean |
44.73 |
0.00 |
1.25 |
0.00 |
48.85 |
|
min |
32.65 |
-18.01 |
0.00 |
-8.45 |
40.96 |
|
25% |
42.07 |
-4.94 |
0.00 |
-0.01 |
46.17 |
|
50% |
44.99 |
0.00 |
0.00 |
0.00 |
48.67 |
|
75% |
47.43 |
4.94 |
0.00 |
0.01 |
50.77 |
|
max |
56.47 |
18.01 |
12.67 |
8.45 |
57.97 |
|
std |
3.89 |
6.58 |
2.66 |
0.47 |
3.59 |
|
pct_estimate |
lead |
pct_3rd_party |
momentum |
|
|
count |
3228 |
3228 |
3228 |
3228 |
|
mean |
43.53 |
0.00 |
5.87 |
0.00 |
|
min |
35.39 |
-8.77 |
0.00 |
-6.28 |
|
25% |
41.06 |
-2.07 |
0.00 |
-0.12 |
|
50% |
43.76 |
0.00 |
8.01 |
0.00 |
|
75% |
46.56 |
2.07 |
8.91 |
0.12 |
|
max |
48.89 |
8.77 |
12.17 |
6.28 |
|
std |
3.22 |
3.63 |
4.05 |
0.45 |
The distributions of the features in both swing_until_20 and swing_24 datasets appear plausible and align with expectations for polling data in swing states.
The pct_estimate values range between approximately 33% and 56% historically and 35% to 49% in 2024, which is reasonable for competitive elections where neither candidate dominates overwhelmingly. The vote_share in the historical dataset has a mean of 48.85%, which is plausible given that swing states often have close to 50-50 splits.
As we’d expect, the lead and momentum variables center around a mean of 0 in both datasets, indicating that leads, lags, gains, and losses between candidates balance out over time. The lead variable seems to be almost perfectly normally distributed, while the momentum is at least symmetrical but has most values closer to the mean.
The historical pct_estimate follows a quite normal distribution with a slight skew to the left, as the mean is at least very close to the median, and the spread captures typical amounts of values within a reasonable range.
In the 2024 data, the poll percentages are centered more closely to the mean. The lead variable has a lower standard deviation in 2024 (3.63) compared to the historical data (6.58), and the range of its values is even less than half of the historical one. These are all indicators of the margins between candidates being closer in 2024, suggesting even tighter races.
In most cycles, there was no third-party candidate gathering any meaningful support, as we can see from the fact that over 75% of the observations have a pct_3rd_party value of 0, with the average being 1.25%. The high numbers in 2024 (median of 8,01%) reflect the strong support independent candidate Robert F. Kennedy had until the end of his campaign in August 2024.
Prediction Strategy for 2024 US Elections
Our prediction strategy will account for the fact that polls are not definitive election results but merely indicators of public sentiment at specific moments. Therefore, we will avoid relying on simple time-series predictions that treat polling data as direct forecasts of outcomes. Instead, we will use a regression-based approach that predicts the election outcome for each polling observation individually, rather than forecasting a timeline of poll data.
Recognizing that each state has its own political landscape, we will build a separate model for each swing state. To prevent data leakage and respect the passage of time, we will ensure that our models are only tested on unseen data—specifically, election cycles that occur after those on which the models were trained. This approach will help us evaluate the models' ability to generalize to future elections accurately.
I chose two evaluation criteria when evaluating the predictive models for election vote shares. Since the winner “takes it all” in each state, the number of correctly predicted winners across the testing cycles is the most important measure to consider.
The Mean Absolute Error (MAE) is the secondary evaluation criterion. It measures the average magnitude of errors between predicted and actual values in the same units as the target variable—in this case, percentage points of vote share. This makes it highly interpretable and directly relevant to our context, as it tells us, on average, how many percentage points our predictions deviate from the actual results.
Finally, we will train each state’s best model on all election cycles up to 2020 and apply it to predict the 2024 election outcomes. We will use time-based weighting with an exponential decay function to transform individual predictions into a single predictive value per state, giving more importance to recent polls.
Choosing the Machine Learning Models
First of all, we import the packages we will need later. This includes all the models we will evaluate, NumPy, as well as the mean_absolute_error.
# Importing models
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression, Ridge, ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.svm import SVR
import catboost
import xgboost as xgb
# Importing other necessary libraries
from sklearn.metrics import mean_absolute_error
import numpy as npTraining the models
Let’s create a workflow to train and evaluate the base models! We will go through the process step by step and then apply it to each state for each test cycle, starting with 2004.
To tailor our models to each state's unique characteristics, we begin by filtering the dataset to include only the data relevant to the state under analysis. This ensures that the model captures state-specific voting patterns and polling data.
# Filter data for the state you're analyzing
data_state = swing_until_20[swing_until_20['state'] == state].copy()We then define a weight function to assign more importance to polls conducted closer to the election date. This exponential decay function decreases the weight of polls as they are further from the election, emphasizing the relevance of recent polling data.
# Define the weight function (using a typical starting k value)
def compute_weight(days_until_election, k):
return np.exp(-k * days_until_election)
# Add weights to the data
data_state['weight'] = compute_weight(data_state['days_until_election'], k=0.1)Next, we split the data into training and testing sets based on election cycles, ensuring that we train on past elections and test on future ones to prevent data leakage. We’ll get to the definition of train_cycles and test_cycle later when we wrap around the loop through the election cycles. We also define the features that will be used for prediction and extract the target variable, which is the actual vote share.
# Split data into training and testing sets based on election cycles
train_data = data_state[data_state['cycle'].isin(train_cycles)]
test_data = data_state[data_state['cycle'] == test_cycle]
# Define features and target variable
features = ['pct_estimate', 'pct_opponent', 'pct_3rd_party', 'lead', 'rolling_avg_7d',
'days_until_election', 'momentum_candidate', 'momentum_opponent', 'momentum',
'is_incumbent_president', 'is_incumbent_vice_president', 'is_incumbent_party',
'candidate_Donald Trump',
'party_DEM', 'party_REP']
X_train = train_data[features]
y_train = train_data['vote_share']
X_test = test_data[features]
y_test = test_data['vote_share']We define a variety of machine learning models to evaluate, including linear regression, ensemble methods, support vector machines, and neural networks. This diverse set allows us to compare different algorithms and select the best-performing model for each state.
# Models to evaluate
models = {
'LinearRegression': LinearRegression(),
'XGBoost': xgb.XGBRegressor(objective='reg:absoluteerror', n_estimators=100, random_state=42),
'CatBoost': catboost.CatBoostRegressor(loss_function='MAE', iterations=100, random_seed=42, verbose=0),
'RandomForest': RandomForestRegressor(n_estimators=100, random_state=42),
'SVR': SVR(kernel='rbf', C=1.0, epsilon=0.1),
'KNeighbors': KNeighborsRegressor(n_neighbors=5),
'MLPRegressor': MLPRegressor(hidden_layer_sizes=(100,), max_iter=500, random_state=42),
'ElasticNet': ElasticNet(alpha=1.0, l1_ratio=0.5, random_state=42),
}Following up, we will loop through the models dictionary. For each model, we train it using the training dataset specific to the current state and then make predictions on the test dataset. This process is repeated for every model to assess their performance comparatively.
for model_name, model in models.items():
# Train the model
model.fit(X_train, y_train)
# Predict on test data
test_data[f'predicted_{model_name}'] = model.predict(X_test)Within the model loop, we aggregate the individual predictions for each party using a lambda function applying the previously computed weights. This results in a single predicted vote share per party, which we then compare to the actual vote share to assess the model's accuracy.
# Aggregate predictions using weights
aggregated_predictions = test_data.groupby('party').apply(
lambda df: np.average(df[f'predicted_{model_name}'], weights=df['weight'])
).reset_index(name='aggregated_prediction')
# Get actual vote shares for comparison
actual_vote_shares = test_data.groupby('party')['vote_share'].mean().reset_index()
comparison = pd.merge(aggregated_predictions, actual_vote_shares, on='party')
comparison.rename(columns={'vote_share': 'actual_vote_share'}, inplace=True)To end the model loop, we calculate the Mean Absolute Error (MAE) between the aggregated predictions and the actual vote shares to quantify the model's performance. We also determine whether the model correctly predicted the winning party in the state and store these results for later analysis.
# Calculate Mean Absolute Error
mae = mean_absolute_error(comparison['actual_vote_share'], comparison['aggregated_prediction'])
# Check if the predicted winner matches the actual winner
predicted_winner = comparison.loc[comparison['aggregated_prediction'].idxmax(), 'party']
actual_winner = comparison.loc[comparison['actual_vote_share'].idxmax(), 'party']
correct_winner = int(predicted_winner == actual_winner)
# Store the results
results_list.append({
'state': state,
'model_name': model_name,
'test_cycle': test_cycle,
'MAE': mae,
'correct_winner': correct_winner
})This entire process is wrapped within two loops: the outer loop iterates over each election cycle (excluding the first one, as there is no prior data to train on), and the inner loop iterates over each swing state. By doing so, we ensure that models are trained and tested appropriately for each state and election cycle, respecting the chronological order of elections to prevent data leakage.
The preface to the code above looks like this:
# Initialize a list to store results
results_list = []
# Define the election cycles
cycles = [2000, 2004, 2008, 2012, 2016, 2020]
for i in range(1, len(cycles)): # The loop starts at index 1, so with the 2nd cycle (2004)
test_cycle = cycles[i]
train_cycles = cycles[:i] # train_cycles = all cycles before the test_cycle
for state in swing_states:
# Filter data for the state you're analyzing, etc. …Overall, this strategy allows us to evaluate multiple models across different states and election cycles, ultimately selecting the best-performing model for each state based on predictive accuracy and the ability to correctly forecast the election winner.
Evaluating the results and each state’s model
After training and testing various machine learning models across different states and election cycles, we move on to evaluating their performance to identify the best models for each state. This evaluation focuses on two key metrics: the number of times each model correctly predicted the winning party (correct_winner) and the average Mean Absolute Error (MAE) of their predictions.
First, we compile all the results collected during the model evaluations into a single DataFrame and aggregate the performance metrics:
# After the loop, create a DataFrame from the results list
results_df = pd.DataFrame(results_list)
# Get the sum of correct_winner and the average MAE for every combination of state and model_name
aggregated_evaluation = results_df.groupby(['state', 'model_name']).agg({
'correct_winner': 'sum',
'MAE': 'mean'
}).reset_index()
# Display the maximum number of correct winner predictions and the minimum MAE for each state
print(aggregated_evaluation.groupby('state')['correct_winner'].max())
print(aggregated_evaluation.groupby('state')['MAE'].min())|
state |
Maximum correct_winner |
Minimum MAE |
|
Arizona |
5 |
1.248966 |
|
Georgia |
5 |
0.770760 |
|
Michigan |
4 |
2.685870 |
|
Nevada |
5 |
2.079582 |
|
North Carolina |
5 |
0.917522 |
|
Pennsylvania |
4 |
2.027426 |
|
Wisconsin |
4 |
2.462907 |
That doesn’t look too bad! In all of the states, there was at least one model predicting 4 out of the 5 earlier elections correctly. In 4 of the states (Arizona, Georgia, Nevada, and North Carolina), we even got some models predicting the correct winner in every cycle. The results for the lowest MAE partly have some room for improvement, though, and differ quite much between the states, averaging at 1.74 percent points and ranging from 0.77 in Georgia to 2.69 in Michigan.
With this aggregated information, we proceed to select the top-performing model for each state. We sort the models based on their ability to predict the correct winner first and only subsequently on their MAE. The chosen models are saved in the dictionary best_models.
# Sort the models for each state by correct_winner (descending) and then by MAE (ascending)
sorted_evaluation = aggregated_evaluation.sort_values(by=['state', 'correct_winner', 'MAE'], ascending=[True, False, True])
# Create a dictionary to store the best model for each state
best_models = {}
# Iterate over each state and get the top model
for state in sorted_evaluation['state'].unique():
top_model = sorted_evaluation[sorted_evaluation['state'] == state].iloc[0]
best_models[state] = top_model['model_name']
best_models{'Arizona': 'RandomForest',
'Georgia': 'ElasticNet',
'Michigan': 'LinearRegression',
'Nevada': 'KNeighbors',
'North Carolina': 'CatBoost',
'Pennsylvania': 'KNeighbors',
'Wisconsin': 'MLPRegressor'}The top models for each state vary a lot, reflecting the unique voting patterns and polling behaviors in each region. Surprisingly, in Michigan the best results are even achieved by using Linear Regression, indicating that a simpler linear approach may suffice there.
At this point, we could use hyperparameter tuning to optimize each machine learning model’s performance. Since this would introduce further methodological questions and take big adjustments to the code, it is out of the scope of this already quite long tutorial. The results of the base models already look promising enough to dare and predict the 2024 election results.
Predicting the Swing States in the 2024 US Elections
In the final stage of our analysis, we utilize the best-performing models for each swing state to predict the 2024 election outcomes. We begin by initializing an empty list to store our predictions.
For each state and its corresponding best model from our previous evaluations, we use the same workflow from before. Only this time, we do not have to loop through election cycles but train on all the historical data from 2000 to 2020 (swing_until_20).
# Initialize a list to store predictions
predictions_list = []
for state, model_name in best_models.items():
# Filter the data for the specific state
state_data_train = swing_until_20[swing_until_20['state'] == state].copy() # Data from 2000 to 2020
state_data_test = swing_24[swing_24['state'] == state].copy() # Data for 2024
# Add weights to the test data
state_data_test['weight'] = compute_weight(state_data_test['days_until_election'], k=0.1)
# Define features
features = [
'pct_estimate',
'pct_opponent',
'pct_3rd_party',
'lead',
'rolling_avg_7d',
'days_until_election',
'momentum_candidate',
'momentum_opponent',
'momentum',
'is_incumbent_president',
'is_incumbent_vice_president',
'is_incumbent_party',
'candidate_Donald Trump',
'party_DEM',
'party_REP'
]
# Split features and target variable
X_train = state_data_train[features]
y_train = state_data_train['vote_share']
X_test = state_data_test[features]
# Train the model on the 2000 to 2020 data
model.fit(X_train, y_train)
# Predict on the 2024 data
state_data_test['predicted_vote_share'] = model.predict(X_test)
# Aggregate predictions using weights
aggregated_predictions = state_data_test.groupby('party').apply(
lambda df: np.average(df['predicted_vote_share'], weights=df['weight'])
).reset_index(name='aggregated_prediction')
# Append predictions to the list
for _, pred_row in aggregated_predictions.iterrows():
predictions_list.append({
'state': state,
'party': pred_row['party'],
'predicted_vote_share': pred_row['aggregated_prediction'],
'model': model_name
})After predicting the vote_share column, aggregating the predictions using the weight function we defined earlier, and appending the predictions to the predictions_list, we consolidate the final predictions into a DataFrame. Additionally, we add a ranking for each state and pivot the predictions by state. Here are the predictions made by our models:
# Convert predictions list to DataFrame
predictions_df = pd.DataFrame(predictions_list)
# Add a rank to predictions_df for each state based on the order of predicted_vote_share
predictions_df['rank'] = predictions_df.groupby('state')['predicted_vote_share'].rank(ascending=False)
# Create a pivot table indexed by state
predictions_pivot = predictions_df.pivot(index='state', columns='party', values='predicted_vote_share')
# Display predictions
print("\n2024 Vote Share Predictions:")
predictions_pivot2024 Vote Share Predictions:
state
DEM
REP
Arizona
49.02
50.31
Georgia
48.95
50.08
Michigan
50.34
48.64
Nevada
49.41
48.54
North Carolina
48.95
50.06
Pennsylvania
49.57
49.20
Wisconsin
49.66
49.41The predictions confirm our estimate of a very close race in the swing states. Our models predict four states to give their majority vote for Kamala Harris (Michigan, Nevada, Pennsylvania, Wisconsin) and 3 to Donald Trump (Arizona, Georgia, North Carolina). The states of Pennsylvania and Wisconsin are expected to be especially tight with the difference between both predicted vote shares being only 0.37 respectively 0.25 percent points.
US Election 2024 Prediction
As mentioned before, we assume that all other states vote for the candidate expected to win, i.e., the “blue” states vote for Kamala Harris, and the “red” states vote for Donald Trump. In order to assess how many electoral votes each candidate gets, we define a dictionary assigning each state and district their number of votes and combine the information in a DataFrame called electoral_votes_df.
# Define the number of electoral votes per state for the 2024 US-Presidential elections
electoral_votes = {
'Alabama': 9, 'Alaska': 3, 'Arizona': 11, 'Arkansas': 6, 'California': 54,
'Colorado': 10, 'Connecticut': 7, 'Delaware': 3, 'District of Columbia': 3,
'Florida': 30, 'Georgia': 16, 'Hawaii': 4, 'Idaho': 4, 'Illinois': 19,
'Indiana': 11, 'Iowa': 6, 'Kansas': 6, 'Kentucky': 8, 'Louisiana': 8,
'Maine': 2, 'Maryland': 10, 'Massachusetts': 11, 'Michigan': 15,
'Minnesota': 10, 'Mississippi': 6, 'Missouri': 10, 'Montana': 4,
'Nebraska': 2, 'Nevada': 6, 'New Hampshire': 4, 'New Jersey': 14,
'New Mexico': 5, 'New York': 28, 'North Carolina': 16, 'North Dakota': 3,
'Ohio': 17, 'Oklahoma': 7, 'Oregon': 8, 'Pennsylvania': 19,
'Rhode Island': 4, 'South Carolina': 9, 'South Dakota': 3,
'Tennessee': 11, 'Texas': 40, 'Utah': 6, 'Vermont': 3, 'Virginia': 13,
'Washington': 12, 'West Virginia': 4, 'Wisconsin': 10, 'Wyoming': 3
}
# Create a DataFrame from the dictionary
electoral_votes_df = pd.DataFrame(list(electoral_votes.items()), columns=['State', 'Electoral Votes'])
# Handle states that divide their votes into multiple districts (Maine and Nebraska)
districts = {'ME-1': 1, 'ME-2': 1, 'NE-1': 1, 'NE-2': 1, 'NE-3': 1}
# Add the districts to the DataFrame
districts_df = pd.DataFrame(list(districts.items()), columns=['State', 'Electoral Votes'])
# Combine the two DataFrames
electoral_votes_df = pd.concat([electoral_votes_df, districts_df], ignore_index=True)Next, we create two lists, harris and trump, which contain the blue and red states, respectively, along with the swing states predicted to be won by each candidate. In the next step, we can filter electoral_votes_df for the states in each list and calculate the sum of electoral votes expected for each candidate.
# Extract states from predictions_df where party is DEM and rank is 1
additional_blue_states = predictions_df[
(predictions_df['party'] == 'DEM') & (predictions_df['rank'] == 1)
].state.tolist()
# Extract states from predictions_df where party is REP and rank is 1
additional_red_states = predictions_df[
(predictions_df['party'] == 'REP') & (predictions_df['rank'] == 1)
].state.tolist()
# Combine blue_states and additional_blue_states into a single list
harris = list(set(blue_states + additional_blue_states))
trump = list(set(red_states + additional_red_states))
# Filter the electoral votes for states in each candidate's list
harris_electoral_votes = electoral_votes_df[electoral_votes_df['state'].isin(harris)]
trump_electoral_votes = electoral_votes_df[electoral_votes_df['state'].isin(trump)]
# Sum the electoral votes
sum_harris_electoral_votes = harris_electoral_votes['electoral_votes'].sum()
sum_trump_electoral_votes = trump_electoral_votes['electoral_votes'].sum()
print(
f'According to the predictions made by the machine learning models, '
f'Kamala Harris will win {sum_harris_electoral_votes} electoral votes '
f'and Donald Trump will win {sum_trump_electoral_votes} electoral votes.'
)According to the predictions made by the machine learning models, Kamala Harris will win 276 electoral votes and Donald Trump will win 262 electoral votes.The prediction is that Kamala Harris will win 276 electoral votes and Donald Trump will win 262 electoral votes. If our assumptions and predictions held true, this is what the electoral map would look like on November 5th:
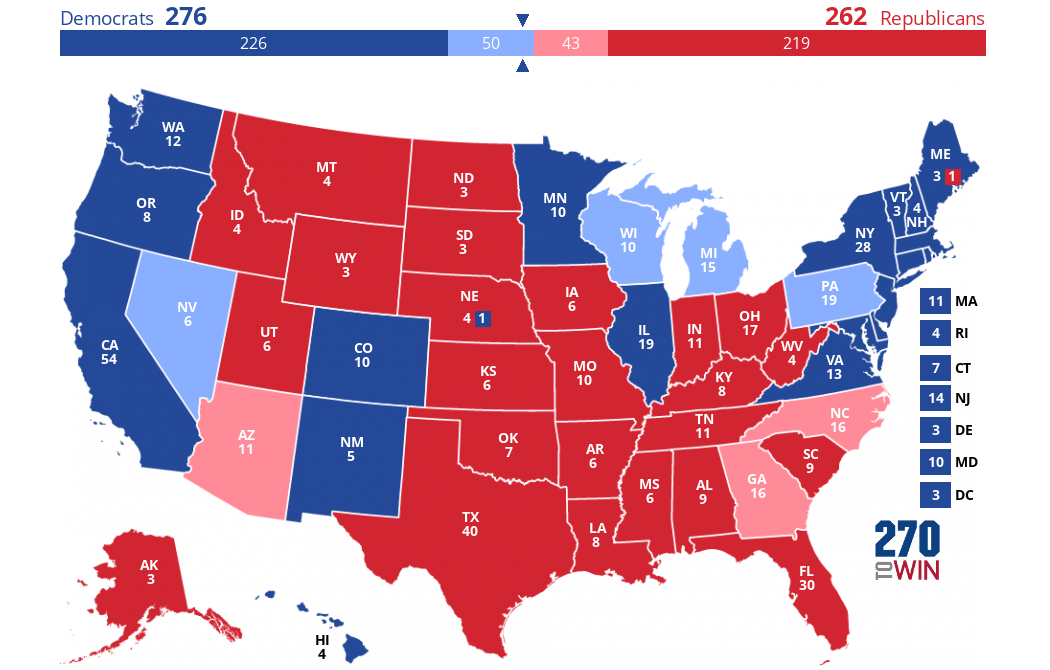
Created using this interactive map creator.
The dark colors represent what we assumed to be “blue” or “red” states. The swing states predicted by us make the difference—they are coloured in a lighter blue or red.
Conclusion
In this project, we used historical polling data to predict the outcome of the 2024 U.S. presidential election. As expected, our models indicate a close race between the leading candidates.
It's important to keep in mind that our analysis was based solely on polling data, which has sometimes been inaccurate in the past and doesn't capture all the nuances of an election. Factors such as polling methodologies, voter turnout, campaign dynamics, economic and demographic circumstances, and unforeseen events were not considered in our models but can significantly impact the actual results.
Nonetheless, this exploration showcases the potential of predictive analytics in understanding complex systems like elections. If you're interested in learning more about predictive analytics using Python, I recommend these resources:

Data Science Editor @ DataCamp | Forecasting things and building with APIs is my jam.



