Bewertung klassischer Testannahmen in R

Bei klassischen parametrischen Verfahren wird oft Normalität und konstante Varianz für den Modellfehlerterm angenommen. Hier werden Methoden zur Untersuchung dieser Annahmen im Rahmen einer ANOVA/ANCOVA/MANOVA diskutiert. Die Regressionsdiagnostik wird unter der multiplen linearen Regression behandelt .

Ausreißer

Da Ausreißer die Normalität und die Homogenität der Varianz stark beeinträchtigen können, werden zunächst Methoden zur Erkennung von abweichenden Beobachtungen beschrieben.

Mit der Funktion aq.plot() im Paket mvoutlier</a > kannst du multivariate Ausreißer identifizieren, indem du die geordneten quadrierten robusten Mahalanobis-Distanzen der Beobachtungen gegen die empirische Verteilungsfunktion des _MD2i aufträgst. Die Eingabe besteht aus einer Matrix oder einem Datenrahmen. Die Funktion erstellt 4 Diagramme und gibt einen booleschen Vektor zurück, der die Ausreißer identifiziert.

# Detect Outliers in the MTCARS Data
library(mvoutlier)
outliers <-
aq.plot(mtcars[c("mpg","disp","hp","drat","wt","qsec")])
outliers # show list of outliers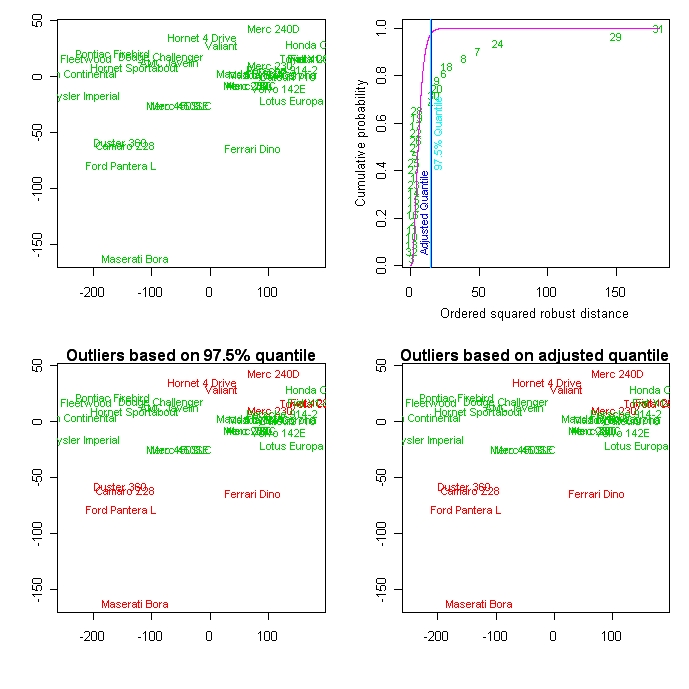

Univariate Normalität

Du kannst die Normalität einer Variablen mithilfe eines Q-Q-Plots bewerten.

# Q-Q Plot for variable MPG
attach(mtcars)
qqnorm(mpg)
qqline(mpg)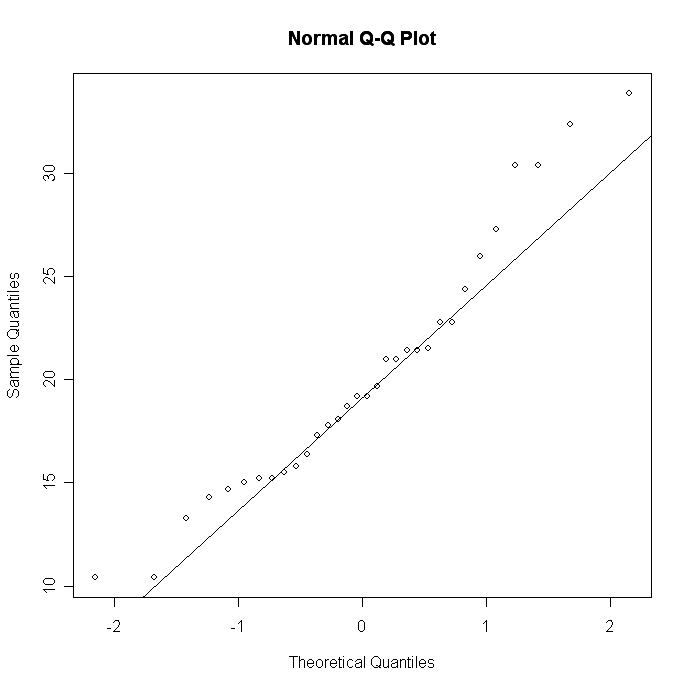

Signifikante Abweichungen von der Linie deuten auf Verstöße gegen die Normalität hin.

Du kannst auch einen Shapiro-Wilk-Test auf Normalität mit der Funktion shapiro.test(x) durchführen, wobei x ein numerischer Vektor ist. Zusätzliche Funktionen zum Testen der Normalität sind im Paket nortest</a > verfügbar.

Multivariate Normalität

MANOVA setzt multivariate Normalität voraus. Die Funktion mshapiro.test( ) im Paket mvnormtest</a > erzeugt den Shapiro-Wilk-Test für multivariate Normalität. Die Eingabe muss eine numerische Matrix sein.

# Test Multivariate Normality

mshapiro.test(M)

Wenn wir p x 1 multivariaten normalen Zufallsvektor haben, dann ist der quadrierte Mahalanobis-Abstand zwischen x und μ eine Chi-Quadrat-Verteilung mit p Freiheitsgraden. Wir können diese Tatsache nutzen, um ein Q-Q-Diagramm zu erstellen, um die multivariate Normalität zu beurteilen.

# Graphical Assessment of Multivariate Normality
x <- as.matrix(mydata) # n x p numeric matrix
center <- colMeans(x) # centroid
n <- nrow(x); p <- ncol(x); cov <- cov(x);
d <-
mahalanobis(x,center,cov) # distances

qqplot(qchisq(ppoints(n),df=p),d,
  main="QQ Plot Assessing Multivariate Normality",
  ylab="Mahalanobis D2")
abline(a=0,b=1)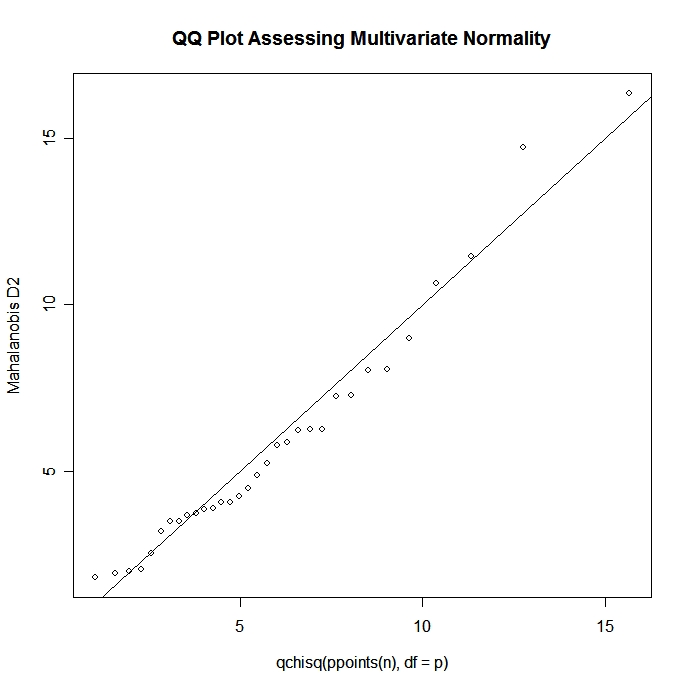

Homogenität der Varianzen

Die Funktion bartlett.test( ) liefert einen parametrischen K-Stichprobentest für die Gleichheit der Varianzen. Mit der Funktion fligner.test( ) kannst du einen nicht-parametrischen Test dafür durchführen. In den folgenden Beispielen ist y eine numerische Variable und G ist die Gruppierungsvariable.

# Bartlett Test of Homogeneity of Variances
bartlett.test(y~G, data=mydata)

# Figner-Killeen Test of Homogeneity of Variances
fligner.test(y~G, data=mydata)

Die Funktion hovPlot( ) im HH-Paket bietet einen grafischen Test der Homogenität der Varianzen auf der Grundlage von Brown-Forsyth. Im folgenden Beispiel ist y ein numerischer Wert und G ein Gruppierungsfaktor. Beachte, dass G vom Typ Faktor sein muss.

# Homogeneity of Variance Plot
library(HH)
hov(y~G, data=mydata)
hovPlot(y~G,data=mydata)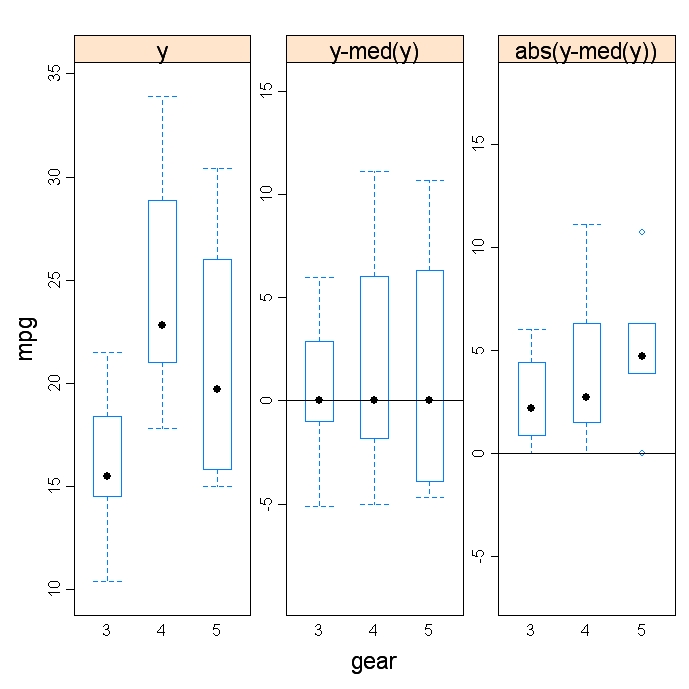

Homogenität von Kovarianzmatrizen

MANOVA und LDF gehen von der Homogenität der Varianz-Kovarianz-Matrizen aus. Die Annahme wird normalerweise mit Box's M getestet. Leider reagiert der Test sehr empfindlich auf Verstöße gegen die Normalität und führt in den meisten typischen Fällen zu einer Ablehnung. Box's M ist über die Funktion boxM im Paket biotools</a > verfügbar.

Zum Üben

Besuche den Kurs Einführung in die Statistik in R</a>, um deine statistischen Kenntnisse weiter auszubauen .