Wahrscheinlichkeitsdiagramme in R
Dieser Abschnitt beschreibt die Erstellung von Wahrscheinlichkeitsdiagrammen in R sowohl für didaktische Zwecke als auch für die Datenanalyse.
Wahrscheinlichkeitsdarstellungen für Unterricht und Demonstration
Als ich als College-Professor Statistik unterrichtete, musste ich früher Normalverteilungen von Hand zeichnen. Sie sahen immer wie Kaninchen aus. Was soll ich sagen?
R macht es einfach, Wahrscheinlichkeitsverteilungen zu zeichnen und statistische Konzepte zu demonstrieren. Im Folgenden findest du einige der gängigsten Wahrscheinlichkeitsverteilungen, die in R verfügbar sind.
| Vertrieb | R-Name | Vertrieb | R-Name |
| Beta | beta | Lognormal | lnorm |
| Binomisch | binom | Negatives Binomial | nbinom |
| Cauchy | cauchy | Normal | norm |
| Chisquare | chisq | Poisson | pois |
| Exponential | exp | Schüler t | t |
| F | f | Uniform | unif |
| Gamma | gamma | Tukey | tukey |
| Geometrisch | geom | Weibull | weib |
| Hypergeometrisch | hyper | Wilcoxon | wilcox |
| Logistik | logis |
Eine umfassende Liste findest du unter Statistische Verteilungen im R-Wiki. Die für jede Verteilung verfügbaren Funktionen folgen diesem Format:
| Name | Beschreibung |
| d name( ) | Dichte oder Wahrscheinlichkeitsfunktion |
| p Name( ) | kumulative Dichtefunktion |
| q Name( ) | Quantilsfunktion |
| R_name_( ) | Zufallsabweichungen |
Zum Beispiel: pnorm(0) =0,5 (die Fläche unter der Standardnormalkurve links von Null). qnorm(0,9) = 1,28 (1,28 ist das 90. Perzentil der Standardnormalverteilung). rnorm(100) erzeugt 100 zufällige Abweichungen von einer Standardnormalverteilung.
Jede Funktion hat spezifische Parameter für diese Verteilung. Zum Beispiel erzeugt rnorm(100, m=50, sd=10) 100 Zufallsabweichungen von einer Normalverteilung mit Mittelwert 50 und Standardabweichung 10.
Du kannst diese Funktionen nutzen, um verschiedene Aspekte von Wahrscheinlichkeitsverteilungen zu demonstrieren. Im Folgenden werden zwei gängige Beispiele genannt.
# Display the Student's t distributions with various
# degrees of freedom and compare to the normal distribution
x <- seq(-4, 4, length=100)
hx <- dnorm(x)
degf <- c(1, 3, 8, 30)
colors <- c("red", "blue", "darkgreen", "gold", "black")
labels <- c("df=1", "df=3", "df=8", "df=30", "normal")
plot(x, hx, type="l", lty=2, xlab="x value",
ylab="Density", main="Comparison of t Distributions")
for (i in 1:4){
lines(x, dt(x,degf[i]), lwd=2, col=colors[i])
}
legend("topright", inset=.05, title="Distributions",
labels, lwd=2, lty=c(1, 1, 1, 1, 2), col=colors)# Children's IQ scores are normally distributed with a
# mean of 100 and a standard deviation of 15. What
# proportion of children are expected to have an IQ between
# 80 and 120?
mean=100; sd=15
lb=80; ub=120
x <- seq(-4,4,length=100)*sd + mean
hx <- dnorm(x,mean,sd)
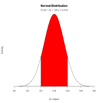
plot(x, hx, type="n", xlab="IQ Values", ylab="",
main="Normal Distribution", axes=FALSE)
i <- x >= lb & x <= ub
lines(x, hx)
polygon(c(lb,x[i],ub), c(0,hx[i],0), col="red")
area <- pnorm(ub, mean, sd) - pnorm(lb, mean, sd)
result <- paste("P(",lb,"< IQ <",ub,") =",
signif(area, digits=3))
mtext(result,3)
axis(1, at=seq(40, 160, 20), pos=0)Einen umfassenden Überblick über die Erstellung von Wahrscheinlichkeitsgrafiken in R findest du in Vincent Zonekynds Probability Distributions.
Anpassen von Verteilungen
Es gibt verschiedene Methoden zur Anpassung von Verteilungen in R. Hier sind einige Optionen.
Mit der Funktion qqnorm( ) kannst du eine Quantil-Quantil-Darstellung erstellen, die die Anpassung der Stichprobendaten an die Normalverteilung bewertet. Allgemeiner ausgedrückt: Die Funktion qqplot( ) erstellt ein Quantil-Quantil-Diagramm für jede theoretische Verteilung.
# Q-Q plots
par(mfrow=c(1,2))
# create sample data
x <- rt(100, df=3)
# normal fit
qqnorm(x);
qqline(x)
# t(3Df) fit
qqplot(rt(1000,df=3), x, main="t(3) Q-Q Plot",
ylab="Sample Quantiles")
abline(0,1)Die Funktion fitdistr( ) im MASS-Paket ermöglicht die Anpassung von univariaten Verteilungen mit maximaler Wahrscheinlichkeit. Das Format ist fitdistr(x, Dichtefunktion), wobei x die Stichprobendaten sind und die Dichtefunktion eine der folgenden ist: "beta", "cauchy", "chi-squared", "exponentiell", "f", "gamma", "geometrisch", "log-normal""lognormal", "logistisch", "negativ binomial", "normal", "Poisson", "t" oder "weibull".
# Estimate parameters assuming log-Normal distribution
# create some sample data
x <- rlnorm(100)
# estimate paramters
library(MASS)
fitdistr(x, "lognormal")Schließlich verfügt R über eine breite Palette von Anpassungsfähigkeitstests, mit denen du prüfen kannst, ob es sinnvoll ist, anzunehmen, dass eine Stichprobe aus einer bestimmten theoretischen Verteilung stammt. Dazu gehören Chi-Quadrat, Kolmogorov-Smirnov und Anderson-Darling.
Weitere Details zur Anpassung von Verteilungen findest du in Vito Riccis Fitting Distributions with R.
Zum Üben
Probiere diesen interaktiven Kurs zur explorativen Datenanalyse aus.