Guía del Bosque del Aislamiento: Explicación e implementación en Python

Hace poco recibí un mensaje de mi banco: 

"Hemos retenido tu tarjeta. ¿Es tuya la transacción por [importe] en [proveedor]?" 

Afortunadamente, sólo era yo comprando por Internet a una hora intempestiva, pero me hizo pensar... ¿cómo marca el banco las transacciones sospechosas entre todos los cientos de miles que procesa al día?

Identificar el fraude es un caso específico de un problema más amplio en aprendizaje automático (AM) denominado detección de anomalías. Aunque hay muchos métodos para resolver este problema, en este blog nos centraremos en uno de los más populares: Bosques de aislamiento.

La detección de anomalías en la práctica

La lucha contra el fraude, la defensa de las redes, la búsqueda de valores atípicos y la detección de equipos defectuosos pueden parecer problemas diferentes. Sin embargo, comparten un rasgo común: no hay etiquetas ni definiciones claras de lo que constituye una anomalía. En muchos casos, las anomalías son raras y sutiles, por lo que son difíciles de identificar en medio de grandes cantidades de datos normales.

Una forma de desarrollar sistemas de detección de anomalías es utilizar predictivo ML. Por ejemplo, podríamos recoger transacciones fraudulentas. Luego, utilizando características como el importe de la transacción, la hora, la ubicación y el tipo de comerciante, podemos construir un modelo que distinga éstas de las transacciones normales. El problema es que este enfoque sólo nos permitirá detectar casos de fraude similares a los que hemos visto en el pasado. 

Los defraudadores cambian a menudo sus estrategias e intentan nuevas formas de cometer fraude. Muchas de estas estrategias serán completamente inesperadas. Por eso métodos no supervisados para detectar anomalías. Funcionan comparando todas las transacciones e identificando las que tienen valores de características inusuales. Lo importante es que esto significa que no tenemos que etiquetar ninguna operación de antemano.

El fraude no es el único comportamiento difícil de clasificar. En la fabricación, las máquinas pueden fallar en cualquier momento de diversas formas inesperadas. En ciberseguridadse descubren y parchean constantemente nuevos ataques. En medicinalos problemas de salud poco frecuentes pueden quedar ocultos entre muchos resultados de pruebas.  Las aplicaciones son infinitas, así que veamos cómo funciona un enfoque no supervisado para detectar estas anomalías. 

¿Qué es un bosque de aislamiento?

Si no lo has adivinado por el nombre los Bosques de Aislamiento son un método basado en árboles. Son similares a los Bosques Aleatorios. Sin embargo, los componentes básicos son diferentes.

Un Bosque Aleatorio utiliza árboles de decisión creados mediante divisiones basadas en la impureza de gini. Esto requiere una variable objetivo, por lo que, en su lugar, los Bosques de Aislamiento utilizan Árboles de Aislamiento. El método utiliza una colección de estos árboles para calcular las puntuaciones de anomalía de cada instancia. 

Árboles de aislamiento

Merece la pena comprender cómo funciona este bloque básico antes de calcular las puntuaciones de anomalía. Supongamos que intentamos detectar transacciones fraudulentas. Para simplificar las cosas, evaluaremos 1000 transacciones (instancias) y consideraremos dos variables de nuestro conjunto de datos: el importe ( x₁) y la hora del día (x₂) de una transacción.

Para crear un Árbol de Aislamiento, empezamos con todas las instancias o una muestra de ellas en el nodo raíz. En Figura 1, abajo, puedes ver que tenemos una muestra de 256 instancias (más adelante hablaremos de ese número).

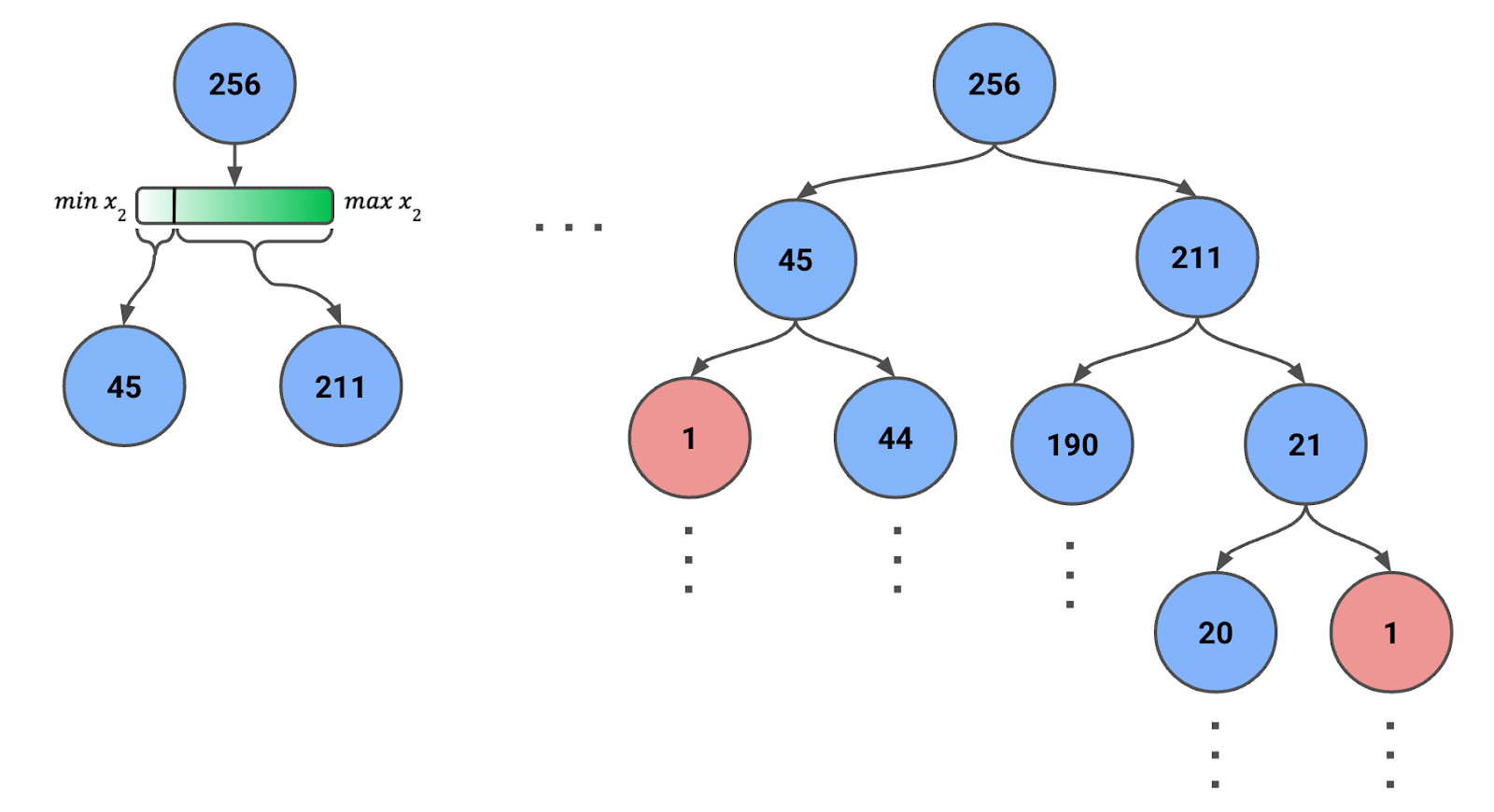
Figura 1: Árbol de Aislamiento creado mediante divisiones aleatorias recursivas. Se indica el número de instancias de cada nodo.

Entonces:

1. Selecciona aleatoriamente una característica (ya sea x₁ o x₂).
2. Selecciona aleatoriamente un valor de división dentro del rango de la característica seleccionada para las instancias actualmente en el nodo.
3. Divide los datos en dos nodos hijos en función del valor de división.
4. Repite el proceso recursivamente para cada nodo hijo hasta que se cumpla una de las siguientes condiciones:
1. Cada nodo hoja sólo tiene una instancia.
2. Se alcanza una profundidad máxima predefinida.

Ten en cuenta que el alcance de la función cambiará en cada paso. Es decir, utilizamos los valores mínimo y máximo de la característica para las instancias del nodo. Este ajuste dinámico garantiza que las divisiones tengan sentido y que los nodos no acaben con cero instancias.

La figura 2 que aparece a continuación nos da una idea de por qué este proceso aísla los valores atípicos. Las instancias A, B y C parecen diferentes de las demás transacciones.

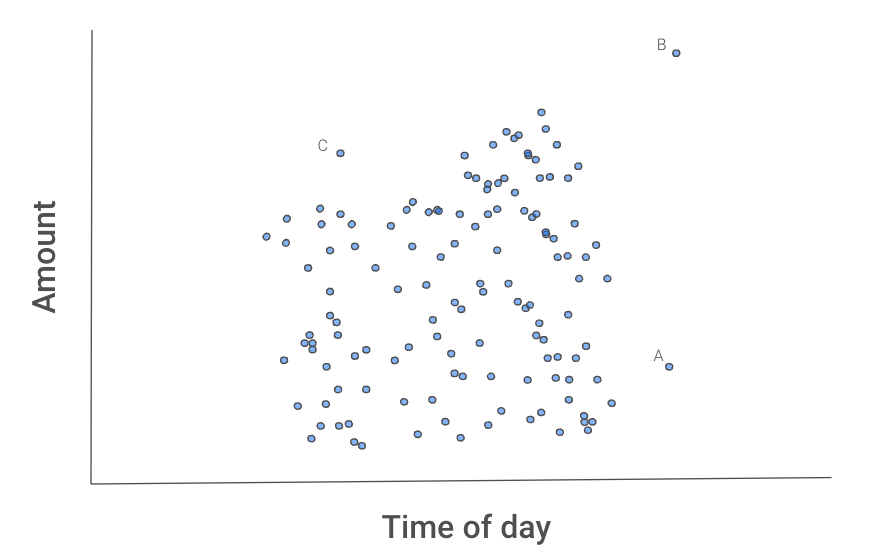
Figura 2: Gráfico de dispersión de las transacciones 

B probablemente se aislará primero, ya que puede separarse de las demás transacciones utilizando una división de cualquiera de las dos funciones.

A tomaría una división de x₂.

C puede llevar más tiempo, ya que tendrías que aislarlo utilizando ambas funciones. Es decir, C tiene una cantidad y una hora normales, pero no una cantidad normal para esa hora del día.

Podemos tener suerte y aislar una de estas instancias en el primer intento. Lo más probable es que necesites varios intentos. Lo importante es que, por término medio, B necesitará menos divisiones que A, A menos divisiones que C, y los tres puntos necesitarán menos divisiones que las demás transacciones. Pero, ¿cómo captamos este comportamiento medio?

Calcular puntuaciones de anomalías 

El número de divisiones necesarias para aislar una anomalía determina la longitud del camino hasta el nodo hoja de la instancia. Cuando un bosque de Árboles de Aislamiento arroja sistemáticamente longitudes de trayectoria más cortas para muestras concretas, es probable que esas muestras sean anomalías. Captamos este comportamiento medio agregando las longitudes de las rutas de todos los árboles, un proceso conocido como cálculo de una puntuación de anomalía.

Para calcular una puntuación de anomalía para una instancia xprimero tenemos que definir algunos valores:

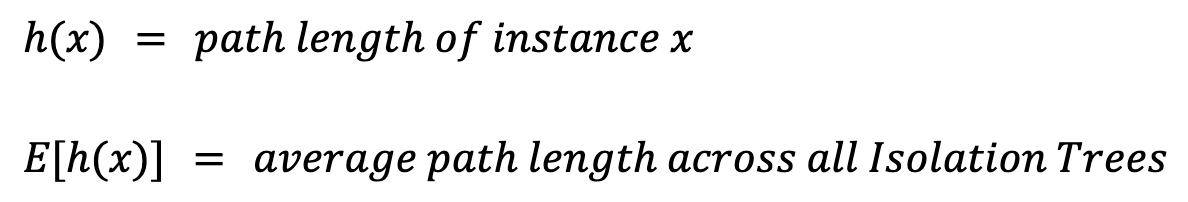
La longitud del camino, h(x), es el número de aristas (divisiones) que hay que recorrer para llegar al nodo hoja de la instancia. Tomar simplemente la media, E[h(x)], dará lugar a problemas. Esto se debe a que los árboles más grandes con más instancias tenderán a tener mayores longitudes de ruta. Esto es cierto incluso para las anomalías. Para tenerlo en cuenta, necesitamos un valor de normalización basado en el tamaño de la muestra n:

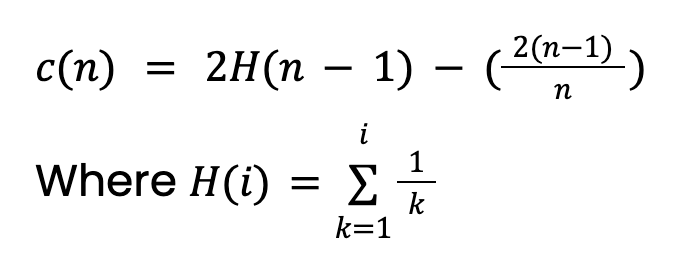
Este valor procede de la teoría de Árboles de búsqueda binaria (BST). Da la longitud media del camino de las búsquedas infructuosas en el BST. Como los Árboles de Aislamiento tienen una estructura equivalente a los BST, tomamos c(n) como la longitud de camino esperada para una instancia (anomalía o no). Ten en cuenta que este valor deberá ajustarse si establecemos una profundidad máxima del árbol.

Por último, podemos calcular nuestra puntuación de anomalía s(x,n):

​La puntuación oscila entre 0 y 1, y al interpretarla, debemos considerar tres escenarios:

• Si un punto es una anomalía, entonces E[h(x)] < c(n) y s → 1
• Si un punto no es una anomalía, entonces E[h(x)] > c(n) y s → 0 
• Si E[h(x)] = c(n) entonces s = 0,5

En otras palabras, cuando la longitud media del camino de una instancia es menor que la longitud media esperada del camino, la puntuación de la anomalía se acercará más a 1. Sin embargo, como veremos al implementar el método, el método Scikit-learn realiza otros ajustes en la puntuación.

Implementación de bosques de aislamiento con Python y Scikit-learn

Abordemos la aplicación paso a paso y empecemos por las importaciones.

Importaciones

Disponemos de paquetes Python estándar para el tratamiento y la visualización de datos (líneas 2-5). También utilizamos la implementación de Scikit-learn del Bosque de Aislamiento (línea 7) y el paquete final se utiliza para importar nuestro conjunto de datos (línea 8).

# Imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.ensemble import IsolationForest
from ucimlrepo import fetch_ucirepo

Conjunto de datos

Cargamos nuestros datos directamente desde el repositorio de aprendizaje automático de la UCI. Estamos utilizando la Calidad del Aire (CC BY 4.0), que contiene 9.358 casos de mediciones de la calidad del aire procedentes de un sensor de una ciudad italiana. En el contexto de este conjunto de datos, una anomalía puede considerarse una lectura del sensor que indica niveles de contaminación inusualmente altos.

# Fetch dataset from UCI repository
air_quality = fetch_ucirepo(id=360)

Limpieza de datos

Hacemos una limpieza de datos antes de aplicar el modelo. Empezamos seleccionando todas las características del conjunto de datos (línea 2) y luego seleccionamos un subconjunto de 4 características (línea 5). Todas ellas son medidas de diferentes sustancias químicas de óxido metálico en el aire (es decir, contaminantes). A continuación, eliminamos las filas que tengan valores perdidos (líneas 8-9). Al final, tenemos 6.941 instancias y puedes ver una instantánea del conjunto de características a continuación.

# Convert to DataFrame
data = air_quality.data.features

# Select features
features = data[['CO(GT)', 'C6H6(GT)', 'NOx(GT)', 'NO2(GT)']]

# Drop rows with missing values (-200)
features = features.replace(-200, np.nan)
features = features.dropna()

print(features.shape)
features.head()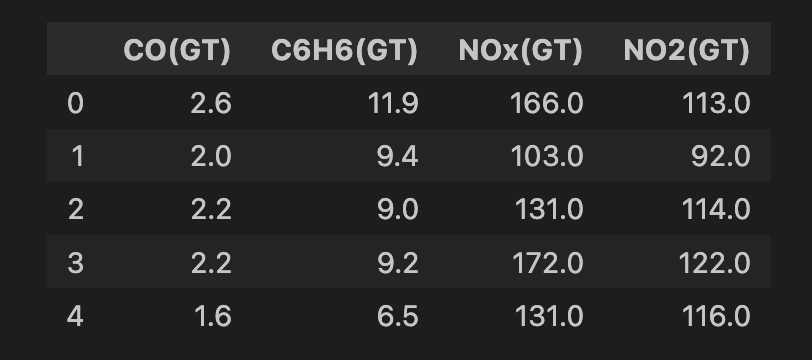

Definir los parámetros de entrenamiento

Lo último que hay que hacer es definir los parámetros utilizados para entrenar el Bosque de Aislamiento. En este caso, utilizaremos los tres valores siguientes: 

• n_estimators es el número de Árboles de Aislamiento utilizados en el conjunto. En el documento Bosque aislado se utiliza un valor de 100. Mediante la experimentación, los investigadores comprobaron que daba buenos resultados en diversos conjuntos de datos. 
• contamination es el porcentaje de puntos de datos que esperamos que sean anomalías. 
• sample_size es el número de instancias utilizadas para entrenar cada Árbol de Aislamiento. Se suele utilizar un valor de 256, ya que nos permite evitar utilizar un criterio de parada de tamaño máximo del árbol. Esto se debe a que podemos esperar tamaños de árbol máximos razonables de log(256) = 8.

El valor contaminación no tiene una justificación sólida como los demás valores. Puede venir de la experiencia previa. Supongamos que en el análisis anterior encontramos que el 1% de las lecturas indican niveles elevados de contaminación.  También podría deberse a la escasez de recursos. Por ejemplo, al analizar las transacciones fraudulentas, puede que sólo tengas tiempo para analizar más a fondo el 5% de todas las transacciones.  Cuando visualicemos las puntuaciones de anomalía, veremos cómo se ajustan utilizando este valor de contaminación.

# Parameters
n_estimators = 100  # Number of trees
contamination = 0.01  # Expected proportion of anomalies
sample_size = 256  # Number of samples used to train each tree

Entrena el Bosque del Aislamiento

Por último, podemos entrenar el Bosque de Aislamiento. Si estás familiarizado con Sklearn, este proceso debería resultarte familiar. Inicializamos el modelo utilizando los parámetros comentados anteriormente (líneas 2-5). A continuación, entrenamos el modelo con nuestro conjunto de características (línea 6).

# Train Isolation Forest
iso_forest = IsolationForest(n_estimators=n_estimators,
                            contamination=contamination,
                            max_samples=sample_size,
                            random_state=42)
iso_forest.fit(features)

Calcular puntuaciones de anomalías

El modelo entrenado tiene dos funciones útiles: 

• decision_function calculará la puntuación de la anomalía de forma similar a lo que comentamos en la sección de teoría. 
• predict proporcionará una etiqueta binaria basada en los valores de contaminación. En nuestro caso, el 1% de las instancias con las peores puntuaciones de anomalía recibirán un valor de -1. A las demás instancias se les da el valor 1.

Añadimos la salida de estas funciones a nuestro conjunto de datos (líneas 2-4). Cuando contamos los valores de anomalía (línea 6), vemos que 70 de las instancias están etiquetadas como anomalías.

# Calculate anomaly scores and classify anomalies
data = data.loc[features.index].copy()
data['anomaly_score'] = iso_forest.decision_function(features)
data['anomaly'] = iso_forest.predict(features)

data['anomaly'].value_counts()

Podemos ir más allá y visualizar todas las puntuaciones de las anomalías. Para ello, utiliza el código que aparece a continuación:

# Visualization of the results
plt.figure(figsize=(10, 5))

# Plot normal instances
normal = data[data['anomaly'] == 1]
plt.scatter(normal.index, normal['anomaly_score'], label='Normal')

# Plot anomalies
anomalies = data[data['anomaly'] == -1]
plt.scatter(anomalies.index, anomalies['anomaly_score'], label='Anomaly')
plt.xlabel("Instance")
plt.ylabel("Anomaly Score")
plt.legend()
plt.show()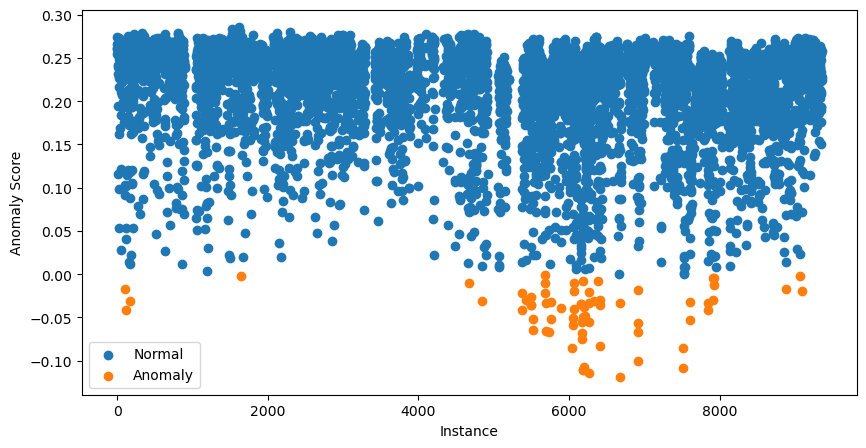

Los 70 casos con las puntuaciones de anomalía más bajas aparecen en naranja. Éstas son nuestras anomalías potenciales y el siguiente paso es investigarlas más a fondo.

Llegados a este punto, puede que estés un poco confuso. ¿No habíamos dicho que las puntuaciones cercanas a 1 indican posibles anomalías? 

Las puntuaciones que ves en el gráfico de dispersión de arriba se han ajustado. Para ello, el paquete calcula primero undesplazamiento . Es el percentil de puntuación de anomalía basado en el valor de contaminación. En nuestro caso, el desplazamiento será el percentil 0,99. Las puntuaciones finales vienen dadas por desplazamiento - puntuación. Hacer esto significa que todas las puntuaciones por debajo de 0 sugieren posibles anomalías.

Más análisis

Utilizando el diagrama de dispersión anterior, podemos identificar posibles anomalías. Sin embargo, esto no nos dice por qué se han clasificado como anomalías. Para ello tendremos que hacer más análisis.

Por ejemplo, en el código siguiente creamos un gráfico de dispersión de todas las instancias trazando su valor de CO(GT) frente a su valor de NO2(GT). También coloreamos los puntos en función de si han sido clasificados como anomalías.

# Visualization of the results
plt.figure(figsize=(5, 5))

# Plot non-anomalies then anomalies
plt.scatter(normal['CO(GT)'], normal['NO2(GT)'], label='Normal')
plt.scatter(anomalies['CO(GT)'], anomalies['NO2(GT)'], label='Anomaly')
plt.xlabel("CO(GT)")
plt.ylabel("NO2(GT)")
plt.legend()
plt.show()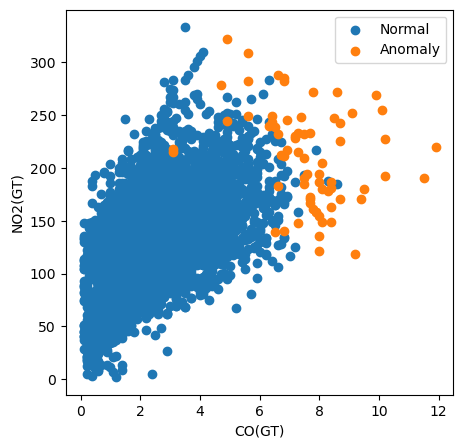

Con este gráfico, podemos ver que la medición del contaminante CO(GT) es especialmente importante. Observa que muchas de las anomalías tienen un valor superior a 6 para esta característica. Sin embargo, esto no explica todas las anomalías. Algunos tienen valores elevados para ambas características y otros no parecen ser anomalías debidas a ninguna de las características de este gráfico.  Esto sugiere que otros contaminantes también han contribuido a la clasificación.

Ventajas del bosque de aislamiento

Esto nos lleva a las principales ventajas de los Bosques de Aislamiento sobre otros métodos de detección de anomalías. La primera es que pueden manejar datos de alta dimensión. Como hemos visto antes, los casos pueden marcarse como anomalías utilizando todas las características, y el método puede funcionar bien con mucho más de cuatro características. Otra ventaja clave es que pueden encontrar anomalías de varios tipos.

A modo de comparación, un método sencillo de detección de anomalías es la puntuación z. Utilizando rasgos individuales, esto clasificará las anomalías en función de lo alejados que estén los valores de los rasgos de su media. Sin embargo, éste es sólo un tipo de anomalía. Este enfoque también supone que las características tienen una distribución normal y nos obliga a evaluar las puntuaciones z de cada característica de nuestro conjunto de datos.

Con los Bosques de Aislamiento, no hacemos ninguna suposición sobre la distribución de una característica. El resultado es que podemos encontrar casos que son anomalías por otros motivos distintos a estar alejados de la media. Como hemos visto, también podemos hacer clasificaciones utilizando todas las características simultáneamente. Esto puede simplificar drásticamente nuestro análisis, especialmente con grandes conjuntos de datos.

Otra consideración es que el Bosque de Aislamiento tiene una complejidad temporal y no está supervisado. Esto lo convierte en un método ideal para detectar anomalías sin conocimiento previo en grandes conjuntos de datos. Esto ocurre a menudo en aplicaciones del mundo real, como la detección del fraudedonde continuamente surgen nuevos tipos de fraude entre un mar de transacciones normales.

Limitaciones del bosque de aislamiento

Una limitación notable del Bosque de Aislamiento es que puede no funcionar tan bien con conjuntos de datos pequeños. Esto tiene que ver con el proceso aleatorio en el que se crean los Árboles de Aislamiento. Siempre existe la posibilidad de que las instancias normales tengan recorridos cortos o, por el contrario, las anomalías tengan recorridos más largos. Con conjuntos de datos pequeños, es más probable que esto ocurra. En otras palabras, para que los Bosques de Aislamiento funcionen, necesitamos suficientes datos para promediar la aleatoriedad.

Otra limitación, como hemos visto, es que el Bosque de Aislamiento sólo puede identificar anomalías potenciales. No nos dice nada sobre por qué ciertos casos son anomalías. Para ello, tenemos que hacer un análisis más detallado. Ahora, la ventaja de identificar anomalías complejas supondrá un reto. En última instancia, puede requerir mucho trabajo y conocimiento del dominio explicar completamente una anomalía.

Conclusión

Exploramos el Bosque de Aislamiento, una potente herramienta para la detección de anomalías en diversos dominios. Hemos visto cómo su enfoque único -aislar las anomalías mediante particiones aleatorias- ofrece ventajas sobre los métodos tradicionales: manejar datos de alta dimensión, identificar patrones de anomalías complejos y garantizar la escalabilidad.

El ejemplo práctico utilizando Python y Scikit-learn demostró la facilidad de uso. 

Aunque el Bosque de Aislamiento puede identificar eficazmente posibles anomalías sin conocimiento previo, también tiene limitaciones, sobre todo cuando se trata de conjuntos de datos más pequeños y su incapacidad para explicar por qué se consideran anomalías instancias concretas.