Multivariate Linear Regression: A Guide to Modeling Multiple Outcomes

Sometimes you need to predict more than one thing at a time, like forecasting both sales and customer churn using the same data.

In this article, I’ll teach you how to multi-task in this way. I’ll teach you about multivariate linear regression. You’ll learn what it is, how it works, when to use it, and how to apply it in practice. By the end, you’ll be ready to apply it to real-world problems. 

If you’re new to regression, you might want to review our Introduction to Regression in R or Introduction to Regression with statsmodels in Python first.

What Is Multivariate Linear Regression?

Multivariate linear regression is a statistical technique that models the relationship between multiple independent variables and multiple dependent variables. It’s sometimes confused with multiple linear regression because it sounds similar, and I’ve gotten them confused before, also. But multiple linear regression uses several predictors to estimate a single outcome, whereas multivariate linear regression is designed for situations where you need to predict more than one outcome at the same time.

Theoretical Foundations and Model Setup

I’ve just given you an outline of what multivariate regression is and when to use it. Let me know get into how the model is structured and what assumptions it relies on.

Matrix representation

Multivariate regression uses a matrix-based setup to model multiple outcomes at the same time:

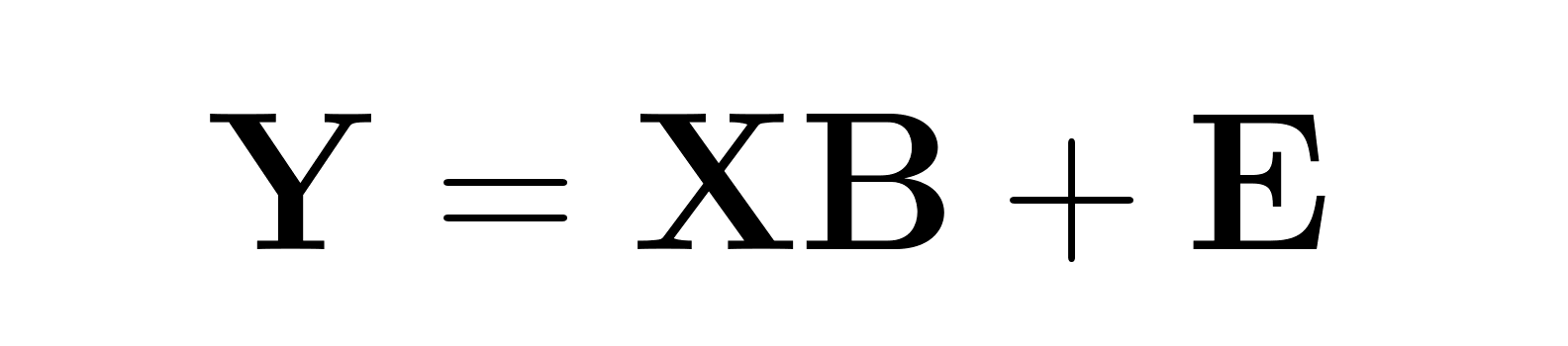
Where:

• Y is an n×p matrix of dependent variables (n observations, p response variables)
• X is an n×(k+1) matrix of independent variables (including intercept)
• B is a (k+1)×p matrix of regression coefficients
• E is an n×p matrix of error terms

This approach recognizes that error terms for different response variables may be correlated, leading to more efficient parameter estimation than separate univariate models. 

Assumptions

Before using the model, it’s important to understand the assumptions that must hold—and what to do if they don’t.

• Linearity: Each predictor should relate linearly to each outcome. Nonlinear relationships bias your results. 
• Independence: Your observations should be independent. If they aren’t (I’m thinking about time series or clustered data), standard errors become unreliable.
• Multivariate normality: The error terms should follow a multivariate normal distribution. Even if this isn't true, your coefficient estimates remain unbiased, but the accuracy of confidence intervals and hypothesis tests can be compromised. While the Shapiro-Wilk test can assess normality for each outcome individually, multivariate normality is best evaluated using dedicated tests like Mardia's test, which account for correlations among residuals.
• Homoscedasticity: The variance of errors should be constant across predictors and outcomes. If not, the model becomes less efficient. 
• No perfect multicollinearity: Your predictors shouldn’t be perfectly correlated. 

If these assumptions don’t hold, you’ll need to adapt. For example, try transforming variables to address nonlinearity or normality issues, switch to weighted least squares to handle heteroscedasticity, or use ridge regression for collinearity problems.

Handling categorical variables

If you’re working with categorical variables, you’ll need to convert them to dummy variables first. 

For a categorical variable with k categories, create k-1 dummy variables. This prevents redundancy, known as the dummy variable trap. The category left out becomes the reference level. Your coefficients will then reflect the difference relative to that baseline. So it’s worth choosing one that makes interpretation straightforward.

Estimation Techniques and Efficiency

With the model structure and assumptions in place, let’s look at how coefficients are estimated, and how different methods compare in terms of efficiency and accuracy.

Ordinary least squares (OLS)

OLS is the default starting point and extends naturally to multivariate settings. It gives unbiased coefficient estimates as long as assumptions are met. While the individual estimates are the same as running separate regressions, the advantage here is that residuals are shared so you can test joint hypotheses across outcomes.

In cases where outcomes are correlated, multivariate OLS captures those relationships, often (but not always) improving overall prediction quality. 

Gauss-Markov theorem

You might be wondering why OLS is so widely used. The Gauss-Markov theorem explains it: Under certain assumptions, OLS is the Best Linear Unbiased Estimator (BLUE). That means it gives you the smallest possible variance among all unbiased linear estimators assuming the usual conditions like no multicollinearity, linear relationships, and constant variance hold.

Weighted least squares (WLS)

But what if those conditions don’t hold, particularly the constant variance one? In this case, I consider WLS. It assigns more weight to observations with lower error variance and less to noisier ones.

WLS tweaks the OLS process by adding a weight matrix. You might estimate weights using residuals from an OLS model or based on theoretical knowledge about your data’s error structure.

Shrinkage methods

Next, let’s turn to scenarios with high-dimensional data or multicollinearity. Shrinkage methods are useful here. They allow some bias in exchange for reduced variance, which often helps with prediction.

Ridge regression adds an L2 penalty (λ||B||²), shrinking all coefficients toward zero. It’s useful when every predictor might contribute something. LASSO applies an L1 penalty that can zero out some coefficients entirely—helpful for variable selection. Elastic net blends both, helping when predictors are correlated while still performing selection.

Model Evaluation and Inference

Now that we’ve covered estimation, let’s turn to evaluating how well your model performs and how to draw meaningful conclusions from it.

Goodness-of-fit

Multivariate R-squared gives you a sense of how much overall variation your model explains across all outcomes. Unlike the univariate version, though, this one often uses the determinant of the residual covariance matrix and might not always stay within 0 to 1.

Adjusted R-squared is especially important in multivariate settings since your parameter count increases quickly with multiple outcomes. It helps avoid overfitting by penalizing complexity.

Visual tools like confidence ellipses can also be helpful. These ellipses show uncertainty in predictions and how outcome variables relate to one another. Circular ellipses suggest independence; elongated ones point to strong correlations.

Hypothesis testing

When you want to know whether your model is doing more than just fitting noise, hypothesis testing is key.

Wilks' Lambda tests whether specific predictors have significant effects across the set of outcomes. It compares error covariance matrices from the full model and a reduced model to determine if removing certain predictors would significantly increase unexplained variance. 

Hotelling’s T² works like a multivariate t-test. It evaluates if a specific predictor influences at least one outcome, considering outcome correlations.

Joint testing helps manage the risk of false positives when testing multiple hypotheses at once. This is useful in multivariate regression, where multiple comparisons can quickly get out of hand.

Model comparison

To decide between models, criteria like AIC and BIC come in handy. Both adjust for complexity, which is especially important when modeling multiple outcomes. AIC focuses more on predictive power, while BIC tends to favor simpler models.

You can also use likelihood ratio tests to compare nested models. These check if adding predictors significantly improves model fit.

Advanced Topics and Use Cases

Standard multivariate regression works well for many problems, but sometimes you'll run into situations that need specialized approaches. Maybe you're dealing with hundreds of predictors, or your variables are influencing each other in ways that violate standard assumptions. Here's how to handle (some of) these trickier scenarios.

Feature selection

When you're working with many predictors, feature selection becomes essential for both performance and also for interpretability. LASSO (this stands for ‘Least Absolute Shrinkage and Selection Operator’) stands out here because it can automatically zero out irrelevant predictors while fitting the model.

Unlike ridge regression, which shrinks all coefficients toward zero but keeps them all, LASSO uses an L1 penalty that creates sparse solutions. This makes it very good when you suspect only a subset of your predictors actually matter.

Dealing with endogeneity

Sometimes your predictors influence your outcomes while simultaneously being influenced by them. I’m thinking about how education affects income, but income also affects access to education. This creates something called endogeneity, which makes standard regression estimates unreliable.

Instrumental variables solve this by using a two-stage process. First, you find an "instrument", meaning a variable that affects your problematic predictor but doesn't directly affect your outcome. Then you use this instrument to predict the clean part of your predictor, and use those predictions in your final regression. This should break or help break the circular relationship and then give you reliable or more reliable estimates.

Implementation in software

Most statistical packages handle multivariate regression, though with different strengths. In Python, sklearn.linear_model.LinearRegression natively supports multiple outcomes for true multivariate regression. In my view, statsmodels provides more detailed statistical output, including hypothesis tests. If you are one of those programmers who prefers the R language, you can just stick with the built-in lm() function for basic multivariate models, or you can use the car package for more sophisticated diagnostics.

Alternatives like PLS

Partial Least Squares (PLS) comes in handy when you have more predictors than observations, or when multicollinearity is causing problems. Instead of using all predictors directly, PLS creates latent variables that capture the most relevant information for predicting your outcomes. This approach works particularly well in fields like chemometrics and bioinformatics, where you might have hundreds or thousands of predictors but relatively few observations.

PLS finds directions in your predictor space that explain both predictor variance and outcome covariance. It's especially useful when prediction accuracy matters more than interpretation. Standard MLR can become unstable with many correlated predictors, but PLS stays well-behaved even in challenging situations.

Confidence ellipses

Simple confidence intervals don't work well for multivariate predictions because they ignore correlations between outcomes. Confidence ellipses show the joint uncertainty for pairs of outcomes, revealing how prediction errors are correlated across different response variables. These ellipses tell you about the relationship structure in your predictions. Circular ellipses mean your outcomes are predicted independently, while elongated ellipses indicate strong correlations.

The orientation of elongated ellipses shows which linear combinations of outcomes have the most and least uncertainty. You can plot these for individual predictions or for parameter estimates, and they're useful when presenting results because they give an intuitive visual representation of how confident you should be in different aspects of your predictions.

Practical Considerations and Example in Python

Moving from theory to practice means dealing with messy data and making sure your model actually works. Here's how to handle the practical side of multivariate regression.

Preprocessing

Before fitting any multivariate model, you'll need to get your data in shape. Scaling and centering are especially important when your predictors have different units. Imagine trying to compare income (in thousands) with age (in years) without standardization. Most algorithms work better when features are on similar scales.

Missing values pose another challenge. You can drop rows with missing data, but this wastes information and can introduce bias. Better approaches include mean imputation for numerical variables or using more sophisticated methods like multiple imputation, which creates several plausible datasets and combines results across them.

Model validation

Cross-validation helps you understand how well your model generalizes beyond your training data. For multivariate regression, k-fold cross-validation works by splitting your data into k groups, training on k-1 groups, and testing on the remaining group. Repeat this k times and average the results to get a robust estimate of performance.

Bootstrapping offers another validation approach that's particularly useful for understanding parameter uncertainty. It creates new datasets by sampling with replacement from your original data, fits models to each bootstrap sample, and examines the distribution of parameter estimates. This tells you how stable your coefficients are and helps build confidence intervals.

Case study

Let's look at a concrete example using a materials testing dataset. Engineers often need to predict multiple properties of concrete—like compressive strength and workability—based on mixture components such as cement content, water ratio, and aggregate type. This makes perfect sense for multivariate regression since these outcomes are related but distinct.

The analysis starts with exploring correlations between mixture components and outcomes, checking for multicollinearity among predictors, and examining whether the relationships look linear. After preprocessing (scaling the mixture ratios and handling any missing measurements), you'd fit the multivariate model and validate it using cross-validation to ensure the predictions hold up on new concrete mixtures.

Code example

Here's a basic workflow that demonstrates the key steps in Python. First, let's set up our data and handle preprocessing:

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error

# Load and prepare data (assuming concrete dataset)
# X: mixture components (cement, water, aggregate, etc.)
# y: multiple outcomes (strength, workability, durability)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

This preprocessing step standardizes all predictors to have mean zero and unit variance, which helps with numerical stability and interpretation.

Next, we'll fit the multivariate model and examine the results:

# Fit multivariate regression
mlr_model = LinearRegression()
mlr_model.fit(X_scaled, y)

# Get coefficients for each outcome
for i, outcome in enumerate(['strength', 'workability', 'durability']):
   coeffs = mlr_model.coef_[:, i]
   print(f"{outcome} coefficients: {coeffs}”)

The LinearRegression model fits a single multivariate regression that considers correlations between all outcomes simultaneously. The coefficients tell you how each mixture component affects each concrete property.

Finally, let's validate the model to check its reliability:

# Cross-validation for each outcome
cv_scores = cross_val_score(mlr_model, X_scaled, y, 
                           cv=5, scoring='neg_mean_squared_error')
print(f"Average CV score: {-cv_scores.mean():.3f}")

# Make predictions on new data
y_pred = mlr_model.predict(X_scaled)
mse_per_outcome = [mean_squared_error(y[:, i], y_pred[:, i]) 
                   for i in range(y.shape[1])]
print(f"MSE per outcome: {mse_per_outcome}")

Cross-validation gives you an honest estimate of how well the model performs on unseen data. The per-outcome MSE scores help you understand which concrete properties are easier or harder to predict accurately.

Limitations and Alternatives

Multivariate linear regression works well for many problems, but it has clear boundaries. The biggest limitation is right there in the name—it assumes linear relationships between predictors and outcomes. When relationships are curved, interaction-heavy, or otherwise nonlinear, MLR will give you biased results. High dimensionality creates another problem: with many predictors relative to observations, the model becomes unstable and prone to overfitting.

Several alternatives can handle these limitations better. Generalized Linear Models (GLMs) extend the framework to non-normal outcomes and allow for different link functions. ANCOVA works well when you have both continuous and categorical predictors with interaction effects. For overfitting issues, regularization methods like ridge and LASSO help, or you can try ensemble methods like random forests that handle nonlinearity and high dimensions more naturally.

Conclusion

Multivariate linear regression gives you a solid way to model multiple related outcomes simultaneously, capturing relationships that separate univariate models would miss. Its main strengths lie in interpretability, statistical testing capabilities, and the ability to handle correlated outcomes efficiently. 

Whether you stick with standard MLR or move to other approaches like regularized regression, partial least squares, and ensemble methods, depends on your data characteristics, sample size, and whether prediction or interpretation matters more for your specific problem.

If you want to build on your skills, our Intermediate Regression with statsmodels in Python course covers multiple explanatory variables and interaction effects, while Generalized Linear Models in R expands your toolkit to handle non-normal distributions like the binomial distribution and the Poisson distribution for count data.