Course
OLS (ordinary least squares) regression is definitely worth learning because it is a huge part of statistics and machine learning. It is used to predict outcomes or analyze relationships between variables, and the applications of those two uses include everything from hypothesis testing to forecasting.
In this article, I will help you understand the fundamentals of OLS regression, its applications, assumptions, and how it can be implemented in Excel, R, and Python. There’s a lot to learn, so when you finish, take our designated regression courses like Introduction to Regression in Python and Introduction to Regression in R, and read through our tutorials, like Linear Regression in Excel.
What is OLS Regression?
OLS regression estimates the relationship between one or more independent variables (predictors) and a dependent variable (response). It accomplishes this by fitting a linear equation to observed data. Here is what that equation looks like:
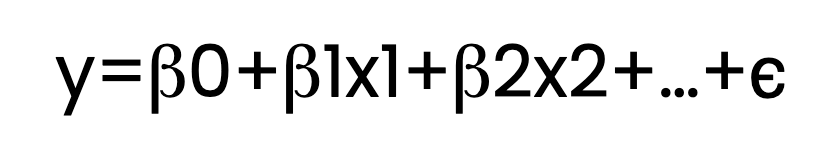
Here:
- y is the dependent variable.
- x1, x2,…, are independent variables.
- β0 is the intercept.
- β1, β2, …, are the coefficients.
- ϵ represents the error term.
In the above equation, I show multiple β terms, like β1 and β2. But just to be clear, the regression equation could contain only one β term besides β0, in which case we would call it simple linear regression. With two or more predictors, such as β1 and β2, we would call it multiple linear regression. Both would qualify as OLS regression if an ordinary least squares estimator is used.
What is the OLS minimization problem?
At the core of OLS regression lies an optimization challenge: finding the line (or hyperplane in higher dimensions) that best fits the data. But what does "best fit" mean? "Best fit" here means minimizing the sum of squared residuals.
Let me try to explain the minimizing problem while also explaining the idea of residuals.
- Residuals Explained: Residuals are the differences between the actual observed values and the values predicted by the regression model. For each data point, the residual tells us how far off our prediction was.
- Why Square the Residuals? By squaring each residual, we ensure that positive and negative differences don't cancel each other out. Squaring also gives more weight to larger errors, meaning the model prioritizes reducing bigger mistakes.
By minimizing the sum of the squared residuals, the regression line become an accurate representation of the relationship between the independent and dependent variables. In fact, by minimizing the sum of squared residuals, our model has the smallest possible overall error in its predictions. To learn more about residuals and regression decomposition, read our tutorial, Understanding Sum of Squares: A Guide to SST, SSR, and SSE.
What is the ordinary least squares estimator?
In the context of regression, estimators are used to calculate the coefficients that describe the relationship between independent variables and the dependent variable. The ordinary least squares (OLS) estimator is one such method. It finds the coefficient values that minimize the sum of the squared differences between the observed values and those predicted by the model.
I'm bringing this up to keep the terms clear. Regression could be done with other estimators, each offering different advantages depending on the data and the analysis goals. For instance, some estimators are more robust to outliers, while others help prevent overfitting by regularizing the model parameters.
How are the OLS regression parameters estimated?
To determine the coefficients that best fit the regression model, the OLS estimator employs mathematical techniques to minimize the sum of squared residuals. One possible method is the normal equation, which provides a direct solution by setting up a system of equations based on the data and solving for the coefficients that achieve the smallest possible sum of squared differences between the observed and predicted values.
However, solving the normal equation can become computationally demanding, especially with large datasets. To address this, another technique called QR decomposition is often used. QR decomposition breaks down the matrix of independent variables into two simpler matrices: an orthogonal matrix (Q) and an upper triangular matrix (R). This simplification makes the calculations more efficient and it also improves numerical stability.
When to Use OLS Regression
How do we decide to use OLS regression? In making that decision, we have to both assess the characteristics of our dataset and we also have to define the specific problem we are trying to solve.
Assumptions of OLS regression
Before applying OLS regression, we should make sure that our data meets the following assumptions so that we have reliable results:
- Linearity: The relationship between independent and dependent variables must be linear.
- Independence of errors: Residuals should be uncorrelated with each other.
- Homoscedasticity: Residuals should have constant variance across all levels of the independent variables.
- Normality of errors: Residuals should be normally distributed.
Serious violations of these assumptions can lead to biased estimates or unreliable predictions. Therefore, we really hav to assess and address any potential issues before going further.
Applications of OLS regression
Once the assumptions are satisfied, OLS regression can be used for different purposes:
- Predictive modeling: Forecasting outcomes such as sales, revenue, or trends.
- Relationship analysis: Understanding the influence of independent variables on a dependent variable.
- Hypothesis testing: Assessing whether specific predictors significantly impact the outcome variable.
OLS Regression in R, Python, and Excel
Let’s now take a look at how to perform OLS regression in R, Python, and Excel.
OLS regression in R
R provides the lm() function for OLS regression. Here's an example:
# Let's create sample data
predictor_variable <- c(1, 2, 3, 4, 5)
response_variable <- c(2, 4, 5, 4, 5)
# We now fit the OLS regression model using the lm() function from base R
ols_regression_model <- lm(response_variable ~ predictor_variable)
# OLS regression model summary
summary(ols_regression_model)Notice how we don’t have to import any additional packages to perform OLS regression in R.
OLS regression in Python
Python offers libraries like statsmodels and scikit-learn for OLS regression. Let’s try an example using statsmodels:
import statsmodels.api as sm
# We can create some sample data
ols_regression_predictor = [1, 2, 3, 4, 5]
ols_regression_response = [2, 4, 5, 4, 5]
# Adding a constant for the intercept
ols_regression_predictor = sm.add_constant(ols_regression_predictor)
# We now fit our OLS regression model
ols_regression_model = sm.OLS(ols_regression_response, ols_regression_predictor).fit()
# Summary of our OLS regression
print(ols_regression_model.summary())OLS regression in Excel
Excel also provides a way to do OLS regression through its built-in tools. Just follow these steps:
Prepare your data
Organize your data into two columns: one for the independent variable(s) and one for the dependent variable. Ensure there are no blank cells within your dataset.
Enable the Data Analysis ToolPak
Go to File > Options > Add-Ins. In the Manage box, select Excel Add-ins, then click Go. Check the box for Analysis ToolPak and click OK.
Run the regression analysis
Navigate to Data > Data Analysis and select Regression from the list of options. Click OK.
In the Regression dialog box:
- Set the Input Y Range to your dependent variable column.
- Set the Input X Range to your independent variable(s).
- Check Labels if your input range includes column headers.
- Select an output range or a new worksheet for the results.
How to Evaluate OLS Regression Models
We’ve now created an OLS regression model. The next step is to see if it's effective by looking model diagnostics and model statistics.
Diagnostic plots
We can evaluate an OLS regression model by using visual tools to assess model assumptions and fit quality. Some options include a residuals vs. fitted values plot, which checks for patterns that might indicate non-linearity or heteroscedasticity, or the Q-Q plot, which examines whether residuals follow a distribution like a normal distribution.
Model statistics
We can also evaluate our model with statistical metrics that provide insights into model performance and predictor significance. Common model statistics include R-squared and adjusted R-squared, which measure the proportion of variance explained by the model. We can also look at the F-statistics and p-values, which test the overall significance of the model and individual predictors.
Train/test workflow
Finally, we should say that data analysts also like to follow a structured process to validate a model's predictive capabilities. This includes a process of data splitting, where the data is divided into training and testing subsets, a training process to fit the model, and then a testing process to evaluate model performance on unseen testing data. This process also might include cross-validation steps like k-fold cross-validation.
Deeper Insights into OLS Regression
Now that we explored the basics of OLS regression, let's explore some more advanced concepts.
OLS regression and maximum likelihood estimation
Maximum likelihood estimation (MLE) is another concept talked about alongside OLS regression, and for good reason. We have spent time so far talking about how OLS minimizes the sum of squared residuals to estimate coefficients. Let’s now take a step back to talk about MLE.
MLE maximizes the likelihood of observing the given data under our model. It works by assuming a specific probability distribution for the error term. This probability distribution is usually a normal, or Gaussian, distribution. Using our probability distribution, we find parameter values that make the observed data most probable.
The reason I’m bringing up maximum likelihood estimation right now is because, in the context of OLS regression, the MLE approach leads to the same coefficient estimates as we get by minimizing the sum of squares errors, provided that the errors are normally distributed.
Interpreting OLS regression as a weighted average
Another fascinating perspective on OLS regression is its interpretation as a weighted average. Prof. Andrew Gelman discusses the idea that the coefficients in an OLS regression can be thought of as a weighted average of the observed data points, where the weights are determined by the variance of the predictors and the structure of the model.
This view provides some insight into how the regression process works and why it behaves the way it does because OLS regression is really giving more weight to observations that have less variance or are closer to the model's predictions. You can also tune into our DataFramed podcast episode, Election Forecasting and Polling, to hear what Professor Gelman says about using regression in election polling.
OLS Regression vs. Similar Regression Methods
Several other regression methods have names that might sound similar but serve different purposes or operate under different assumptions. Let's take a look at some similar-sounding ones:
OLS vs. weighted least squares (WLS)
WLS is an extension of OLS that assigns different weights to each data point based on the variance of their observations. WLS is particularly useful when the assumption of constant variance of residuals is violated. By weighting observations inversely to their variance, WLS provides more reliable estimates when dealing with heteroscedastic data.
OLS vs. partial least squares (PLS) regression
PLS combines features of principal component analysis and multiple regression by extracting latent variables that capture the maximum covariance between predictors and the response variable. PLS is advantageous in situations with multicollinearity or when the number of predictors exceeds the number of observations. It reduces dimensionality while simultaneously maximizing the predictive power, which OLS does not inherently address.
OLS vs. generalized least squares (GLS)
Similar to WLS, GLS generalizes OLS by allowing for correlated and/or non-constant variance of the residuals. GLS adjusts the estimation process to account for violations of OLS assumptions regarding the residuals, providing more efficient and unbiased estimates in such scenarios.
OLS vs. total least squares (TLS)
Also known as orthogonal regression, TLS minimizes the perpendicular distances from the data points to the regression line, rather than the vertical distances minimized by OLS. TLS is useful when there is error in both the independent and dependent variables, whereas OLS assumes that only the dependent variable has measurement error.
Alternatives to OLS Regression
When the relationship between variables is complex or nonlinear, non-parametric regression methods offer flexible alternatives to OLS by allowing the data to determine the form of the regression function. All of the previous examples (the "similar-sounding" ones) belong to the category of parametric models. But non-parametric models could also be used when you want to model patterns without the constraints of parametric assumptions.
| Method | Description | Advantages | Common Use Cases |
|---|---|---|---|
| Kernel Regression | Uses weighted averages with a kernel to smooth data. | Captures nonlinear relationships Flexible smoothing |
Exploratory analysis Unknown variable relationships |
| Local Regression | Fits local polynomials to subsets of data for a smooth curve. | Handles complex patterns Adaptive smoothness |
Trend visualization Scatterplot smoothing |
| Regression Trees | Splits data into branches to fit simple models in each segment. | Easy to interpret Handles interactions |
Segmenting data Identifying distinct data regimes |
| Spline Regression | Uses piecewise polynomials with continuity at knots to model data. | Models smooth nonlinear trends Flexible fitting |
Time series Growth curves |
Final Thoughts
OLS regression is a fundamental tool for understanding data relationships and making predictions. By mastering OLS, you'll build a solid foundation for exploring advanced models and techniques. Explore DataCamp’s courses on regression in R and Python to expand your skill set: Introduction to Regression with statsmodels in Python and Introduction to Regression in R). Also, consider our very popular Machine Learning Scientist in Python career track.
Become an ML Scientist

I'm a data science writer and editor with contributions to research articles in scientific journals. I'm especially interested in linear algebra, statistics, R, and the like. I also play a fair amount of chess!
OLS Regression FAQs
What is OLS regression?
Ordinary Least Squares (OLS) regression is a statistical method used to estimate the relationship between one or more independent variables and a dependent variable. It does this by fitting a linear equation that minimizes the sum of the squared differences between the observed and predicted values, making it a fundamental tool in statistics and machine learning for prediction and analysis.
What are the limitations of OLS regression?
OLS regression assumes a linear relationship, which may not capture complex patterns in the data. It is sensitive to outliers, which can skew results, and struggles with multicollinearity, where independent variables are highly correlated. Additionally, OLS requires that all assumptions (linearity, independence, homoscedasticity, normality) are met; violations can lead to biased or inefficient estimates.
Can OLS regression be used for causal inference?
While OLS regression can identify associations between variables, establishing causation requires careful consideration of the study design and potential confounders. OLS alone does not prove causality. To make causal inferences, additional methods such as randomized controlled trials, instrumental variables, or propensity score matching are often necessary alongside OLS regression.
