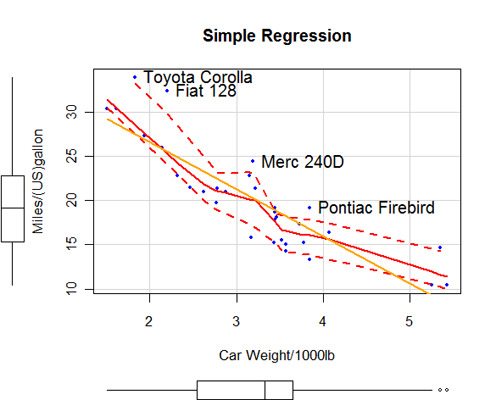
Cette section décrit les statistiques de base (et celles qui le sont moins). Il comprend du code permettant d'obtenir des statistiques descriptives, des comptages de fréquences et des tableaux croisés (y compris des tests d'indépendance), des corrélations(pearson, spearman, kendall, polychorique), des tests t (avec des variances égales et inégales), des tests non paramétriques de différences entre groupes (Mann Whitney U, Wilcoxon Signed Rank, Kruskall Wallis Test, Friedman Test), la régression linéaire multiple (y compris les diagnostics, la validation croisée et la sélection des variables), l'analyse de la variance (y compris ANCOVA et MANOVA) et les statistiques basées sur le rééchantillonnage.

Étant donné que les analyses de données modernes impliquent presque toujours des évaluations graphiques des relations et des hypothèses, des liens vers des méthodes graphiques appropriées sont fournis tout au long du document.

Il est toujours important de vérifier les hypothèses du modèle avant de faire des déductions statistiques. Bien qu'il soit quelque peu artificiel de séparer la modélisation de la régression et le cadre de l'ANOVA à cet égard, de nombreuses personnes apprennent ces sujets séparément, et j'ai donc suivi la même convention ici.

Les diagnostics de régression couvrent les valeurs aberrantes, les observations influentes, la non-normalité, la variance d'erreur non constante, la multicolinéarité, la non-linéarité et la non-indépendance des erreurs. Les hypothèses de test classiques pour l'ANOVA/ANCOVA/MANCOVA comprennent l'évaluation de la normalité et de l'homogénéité des variances dans le cas univarié, et la normalité multivariée et l'homogénéité des matrices de covariance dans le cas multivarié. L'identification des valeurs aberrantes multivariées est également envisagée.

L'analyse de puissance fournit des méthodes d'analyse de puissance statistique et d'estimation de la taille de l'échantillon pour une variété de plans.

Enfin, deux fonctions qui contribuent à un traitement efficace(avec et par) sont décrites.

Statistiques avancées

Cette section décrit des méthodes statistiques plus avancées. Il s'agit notamment de découvrir et d'explorer des relations complexes à plusieurs variables entre les variables. Des liens vers des méthodes graphiques appropriées sont également fournis tout au long du document.

Il est difficile d'ordonner ces sujets de manière directe. J'ai choisi les titres suivants (certes arbitraires).

Modèles prédictifs

Parmi les modèles prédictifs, nous avons les modèles linéaires généralisés (y compris la régression logistique, la régression de poisson et l'analyse de survie), l'analyse de la fonction discriminante (à la fois linéaire et quadratique) et la modélisation des séries chronologiques.

Modèles à variables latentes

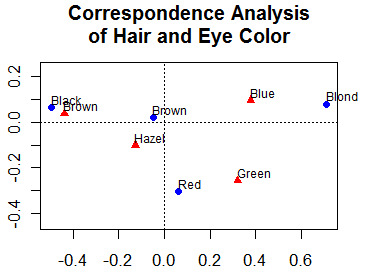
Il s'agit notamment de l'analyse factorielle (composantes principales, analyse factorielle exploratoire et confirmatoire), de l'analyse des correspondances et de l'échelonnement multidimensionnel(métrique et non métrique).

Méthodes de partitionnement

L'analyse des clusters comprend des approches de partitionnement (k-means), d'agglomération hiérarchique et de modélisation. Les méthodes basées sur les arbres (qui auraient facilement pu être classées dans la catégorie des modèles prédictifs !) comprennent les arbres de classification et de régression, les forêts aléatoires et d'autres méthodes de partitionnement.

Autres outils

Cette section comprend des outils très utiles, notamment le bootstrap en R et la programmation de l'algèbre matricielle (pensez à MATRIX dans SPSS ou à PROC IML dans SAS).

Aller plus loin

Pour pratiquer les statistiques en R de manière interactive, essayez ce cours sur l'introduction aux statistiques.

Essayez le cours Apprentissage supervisé en R qui comprend un exercice avec Random Forests.