Bias-Variance Tradeoff: How Models Fail in Production

The bias-variance tradeoff explains why model performance isn't just about complexity or accuracy, but instead it’s about finding the sweet spot where your model generalizes well to unseen data without oversimplifying the problem or overfitting to your training set.

In this article, I'll explain what bias and variance actually mean in machine learning, how they trade off against each other, and why understanding this tradeoff helps you build more robust models.

If you’re new to machine learning, our How to Learn Machine Learning in 2026 article will help you become proficient in no time.

What Is Bias?

Bias is the error that comes from making overly simple assumptions about your data. It has nothing to do with prejudice, at least not when it comes to machine learning.

When a model has high bias, it means the model is too rigid to capture the actual patterns in your data. Think of it like trying to fit a straight line through data that clearly curves: No matter how you adjust that line, it'll never match the real shape.

This is called underfitting.

A high-bias model oversimplifies the problem. It assumes relationships are simpler than they actually are, so it misses important patterns that would help it make accurate predictions.

Imagine you're predicting house prices based on square footage, number of bedrooms, location, and age of the house. A high-bias model might only use square footage and ignore everything else. It assumes that square footage alone determines price, which is way too simple.

The result is a model that performs poorly on both training data and new data because it can't capture the complexity of real house prices.

Linear regression with few features is a classic high-bias model. Decision trees with very limited depth also tend to have high bias because they can't split the data enough times to find nuanced patterns.

High bias means your model isn't learning enough from the data, but is instead making the problem too simple to solve with a good degree of accuracy.

What Is Variance?

Variance measures how sensitive your model is to the specific training data you use.

It has nothing to do with the statistical measure of data spread. In machine learning, variance describes model behavior, not data distribution.

When a model has high variance, small changes in your training data lead to big changes in the model's predictions. In other words, when you train the same model on two slightly different datasets, you'll get wildly different results.

This is called overfitting.

A high-variance model is too flexible. It learns not just the real patterns in your data but also the noise and random fluctuations that don't generalize to new data. The model essentially memorizes the training examples instead of learning the underlying relationships.

Imagine you're still predicting house prices, but now you're using a complex model with hundreds of parameters. It might learn that houses on Oak Street always sell for exactly $427,350 because that's what happened in your training data.

The result is a model that performs great on training data but terrible on new data because it learned quirks specific to the training set.

Deep neural networks and decision trees with unlimited depth are classic high-variance models. They have enough flexibility to fit almost any pattern, including the meaningless ones.

High variance means your model is learning too much from the data. It's fitting the noise along with the signal, which makes it unstable and unreliable on new examples.

Bias vs. Variance: Key Differences

Bias and variance are two completely different sources of prediction error. Once you understand the distinction, you’ll be faster to diagnose what's wrong with your model.

• Bias comes from your model's assumptions. It's about the algorithm you chose, the features you included, and how you structured the problem. A linear regression model assumes linear relationships, so it has bias when the real relationship is nonlinear. This error exists before you even look at your training data.
• Variance comes from sensitivity to training data. It's about how much your model changes when you train it on different samples from the same population. A model with high variance learns different patterns from slightly different training sets, which makes its predictions unstable.

Here's how bias and variance affect prediction error:

• High bias means your model makes consistent mistakes in the same direction. It always underpredicts or always overpredicts certain patterns because it can't represent the true relationship. The errors are systematic and predictable.
• High variance means your model makes inconsistent mistakes that change with the data. Train it on Monday's data and it predicts one thing. Train it on Tuesday's data and it predicts something completely different. The errors are random and unpredictable.

The problem is that reducing one usually increases the other.

When you make your model more complex to reduce bias, you increase its flexibility. That flexibility makes it more sensitive to training data, which increases variance. When you simplify your model to reduce variance, you remove its ability to capture complex patterns, which increases bias.

This inverse relationship is why you can't just minimize both at the same time. Instead, you have to find the balance that gives you the lowest total error.

What Is the Bias-Variance Tradeoff?

The bias-variance tradeoff describes the tension between these two error sources - when you decrease one, you almost always increase the other.

Think of it like this: you're trying to hit a target, but you have two problems working against each other. You can aim more carefully (reduce bias), but that makes you more sensitive to wind and hand tremors (increase variance). Or you can use a simpler, more stable shooting stance (reduce variance), but that limits your precision (increase bias).

Model complexity is at the center of this tradeoff.

When you use a simple model with few parameters, you get high bias and low variance. The model makes consistent assumptions and doesn't change much with different training data, but it can't capture complex patterns.

When you use a complex model with many parameters, you get low bias and high variance. The model can represent intricate relationships, but it becomes unstable and overly sensitive to which specific examples you train it on.

Here's the conceptual curve that explains this:

• On the left side (simple models): Training error is high because the model underfits. Test error is also high because the model misses real patterns.
• In the middle (balanced models): Both training and test errors are low. The model captures real patterns without memorizing noise. This is your sweet spot.
• On the right side (complex models): Training error is very low because the model fits everything. Test error is high because the model has learned noise.

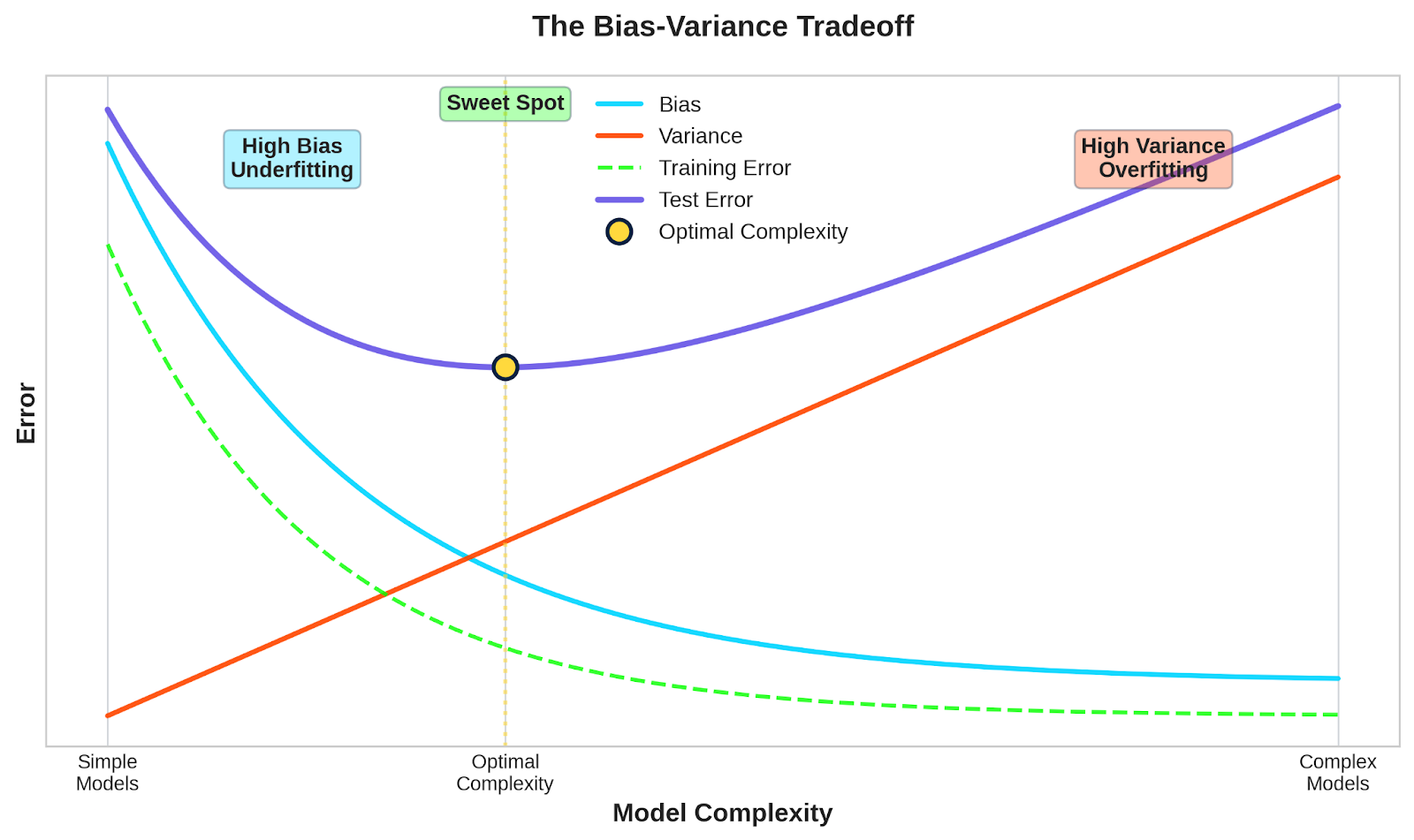
Bias-variance tradeoff curve

You're looking for the point where their combined effect gives you the lowest test error.

There's no single "perfect" model that works for every problem. The optimal balance depends on your data, your problem complexity, and how much training data you have. More data generally lets you use more complex models without overfitting, shifting the sweet spot to the right.

A Simple Bias-Variance Tradeoff Example

Let me make this concept concrete with a real scenario that shows how bias and variance play out in practice.

Imagine you're building a model to predict apartment rental prices in a city. You have features like square footage, number of bedrooms, neighborhood, distance to subway, building age, and amenities.

Simple model: Linear regression with one feature

You decide to use only square footage to predict price with a simple linear regression.

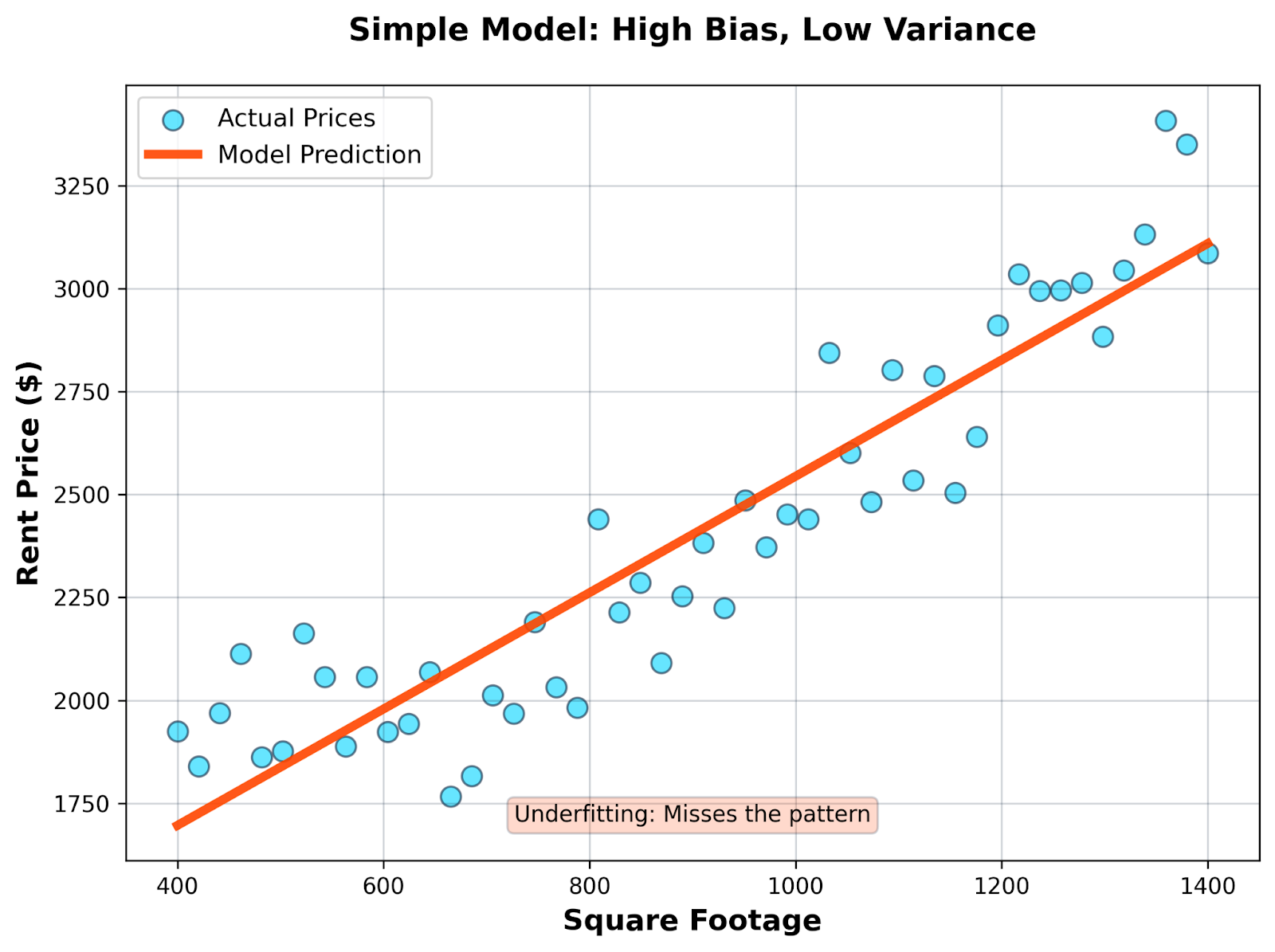
Simple model

• What happens: The model draws a straight line through your data points. It predicts that every 100 square feet adds a fixed dollar amount to the rent, regardless of location or other factors.
• The outcome: This model has high bias and low variance. It consistently underpredicts luxury apartments and overpredicts studio apartments because it can't capture the complex relationship between size and price in different neighborhoods. But if you train it on different samples of apartments, you'll get roughly the same line each time - it's stable but inaccurate.

Complex model: Deep neural network with all features

Now you build a deep neural network with multiple hidden layers using all available features, plus engineered features like neighborhood crime rates, walkability scores, and proximity to parks.

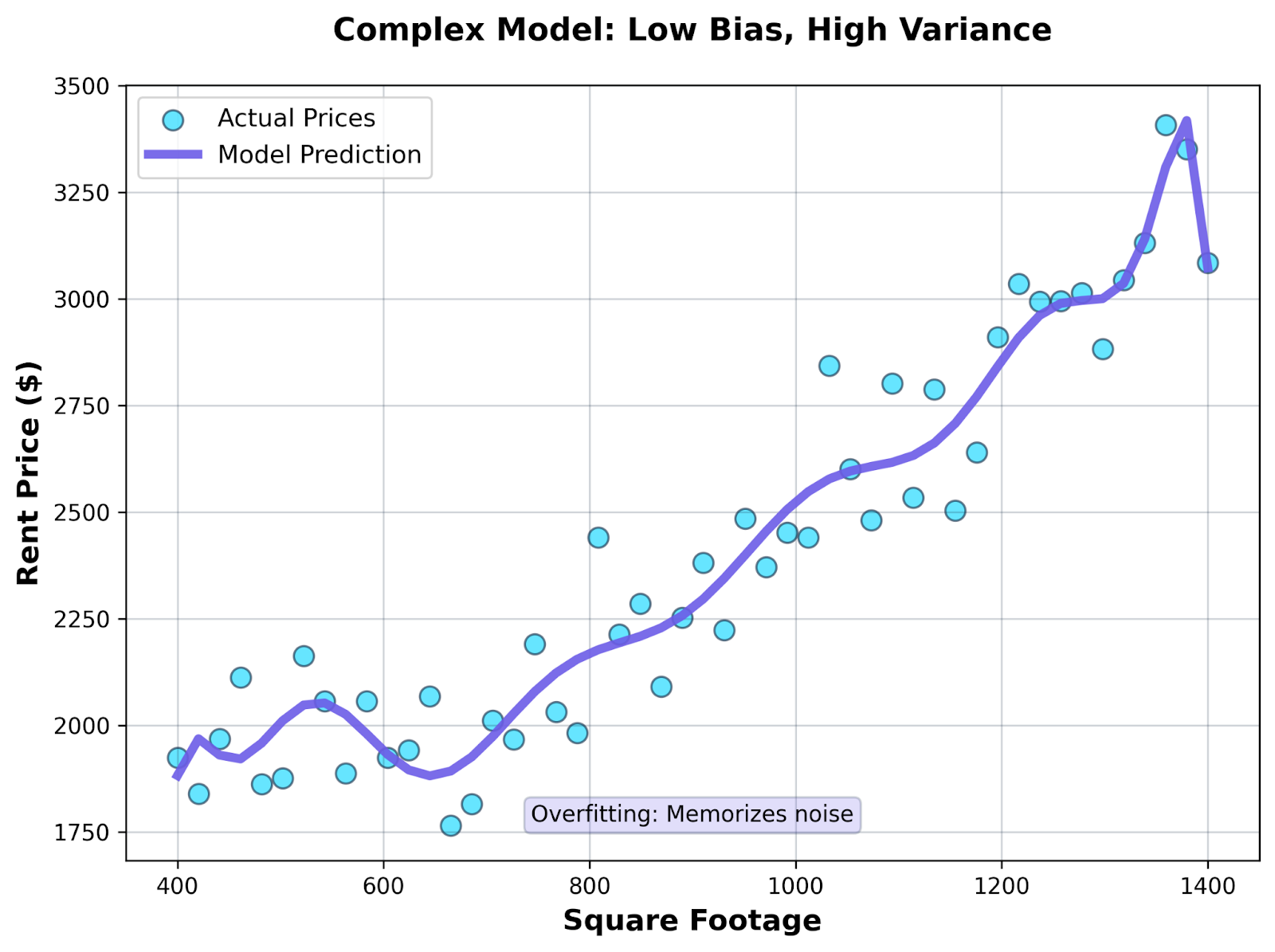
Complex model

• What happens: The network learns intricate patterns. It might discover that apartments on the 5th floor in your specific training data always rent for exactly $2,847, or that units facing north on Oak Street go for 37% higher rent than those that face south.
• The outcome: This model has low bias and high variance. It fits your training data almost perfectly and captures every detail and fluctuation. But those patterns don't generalize - they're artifacts of your specific sample. Train it on a different set of apartments, and it learns completely different patterns. The predictions are unstable and unreliable on new data.

Balanced model: Regularized regression with key features

You use regularized regression (like Ridge or Lasso) with a carefully selected subset of features: square footage, bedrooms, neighborhood category, and distance to transit.

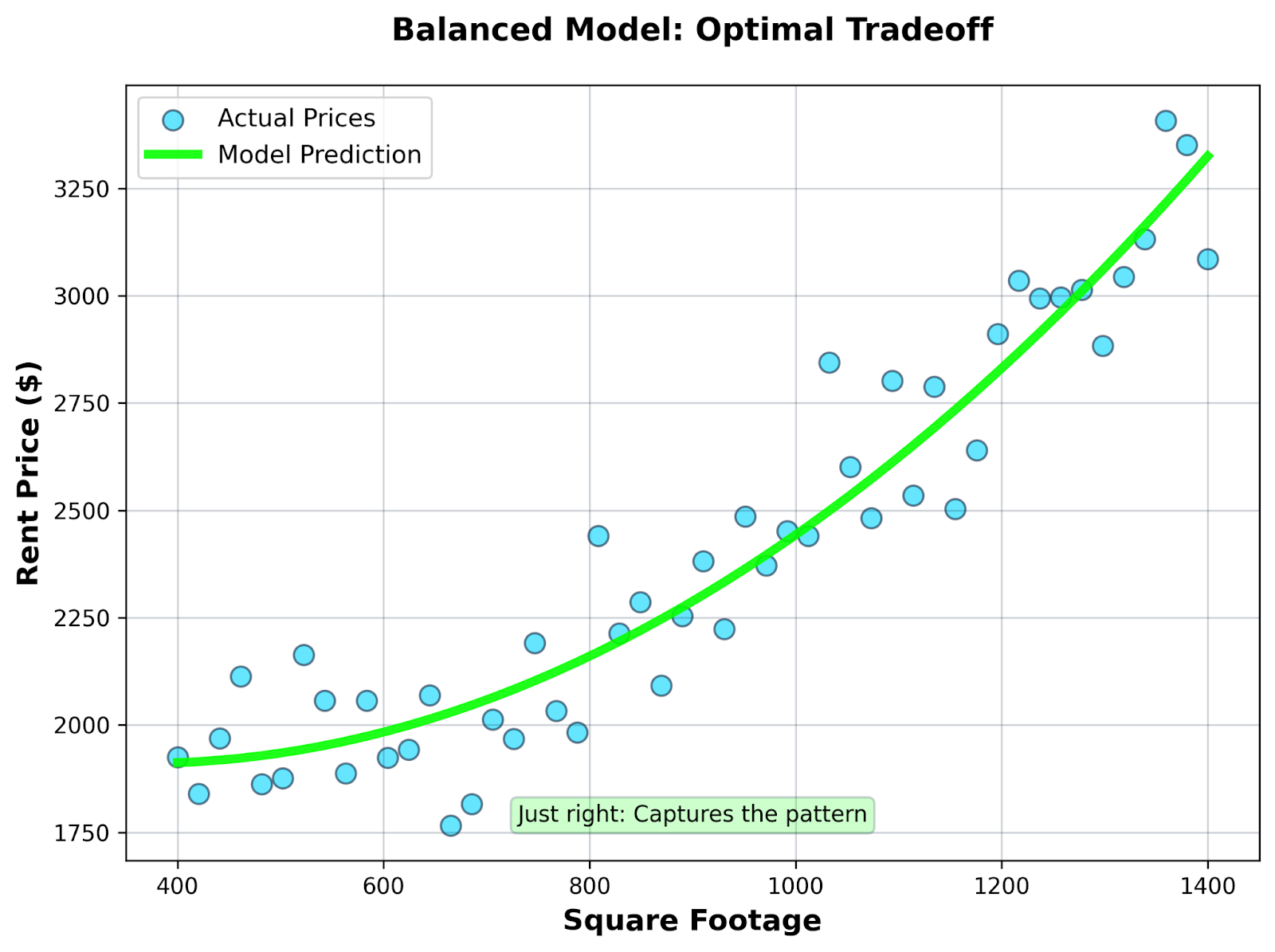
Balanced model

• What happens: The model captures the main relationships without memorizing noise. It learns that size and location matter, but it doesn't obsess over every tiny fluctuation in the training data.
• The outcome: This model balances bias and variance. It's flexible enough to capture real patterns but constrained enough to avoid overfitting. Training error is moderate, but test error is low - which is what actually matters for predictions on new apartments.

The balanced model won't perfectly fit your training data, and that's exactly the point.

Bias-Variance Tradeoff in Machine Learning Models

Different machine learning algorithms naturally lean toward either high bias or high variance. You need to understand these tendencies to pick the right tool for your problem.

Linear models

Linear regression and logistic regression sit on the high-bias end of the spectrum.

These models assume relationships are linear - one feature changes, the output changes by a fixed amount. When your data has nonlinear patterns, curved relationships, or complex interactions between features, linear models can't capture them.

The upside is stability. Train a linear model on different samples of your data, and you'll get similar coefficients each time. Low variance, but potentially high bias if the real relationship isn't linear.

Decision trees

Decision trees can behave differently depending on how you configure them.

A shallow tree with only a few splits acts like a simple model - high bias, low variance. It makes broad generalizations and can't capture fine-grained patterns.

A deep tree with no depth limit becomes extremely flexible. It keeps splitting until each leaf contains just a few data points, which means it memorizes your training data. Low bias, but sky-high variance - the tree structure changes dramatically with different training samples.

This is why random forests work so well. They average predictions from many trees, which reduces the variance problem while keeping bias low.

K-nearest neighbors

KNN's bias-variance balance depends entirely on your choice of k.

When k is small (like k=1 or k=3), the model has high variance. It bases predictions on just a few nearby points, so it's extremely sensitive to which specific examples are in your training set. Small changes in training data lead to completely different predictions.

When k is large (like k=50 or k=100), the model has high bias. It averages over so many neighbors that it smooths out local patterns and misses important details in the data.

The optimal k value is somewhere in the middle, balancing these two extremes.

Neural networks

Neural networks are naturally high-variance models because they have so many parameters to learn.

A network with multiple layers and hundreds of neurons can represent incredibly complex functions. This flexibility means low bias - the network can learn almost any pattern. But it also means high variance - the exact weights you learn depend heavily on your specific training data, initialization, and training process.

This is why neural networks need large datasets to work well. More training data helps stabilize the learning process and reduces variance. It's also why techniques like dropout, batch normalization, and early stopping exist - they're all designed to control variance and prevent overfitting.

Smaller networks with fewer layers and neurons have higher bias but lower variance, while larger networks have lower bias but higher variance.

How Model Complexity Affects Bias and Variance

Unfortunately, model complexity isn't a single number you can measure. It's about how flexible your model is in fitting different patterns.

Complexity comes from multiple sources, such as more features, more layers in a neural network, deeper decision trees, polynomial terms in regression, or lower k values in KNN. The common thread is that they give your model more freedom to fit intricate patterns in the data.

When you add parameters, you're giving your model more ways to represent relationships in your data. A linear model with 3 features can only draw a flat plane through your data. If you add polynomial terms and interaction features, it can bend and curve to match more complex patterns. The model's assumptions become less restrictive, which means lower bias.

But this flexibility comes at a cost, ie, an increase in variance.

More parameters mean more values to learn from your training data. Each parameter gets tuned to fit your specific training examples, which makes the model more sensitive to which examples you happened to include. When you change a few training samples, all those parameters shift to accommodate the new data. The model becomes unstable.

This is why training error alone is misleading and dangerous.

As you increase complexity, training error will always decrease. Your model fits the training data better and better, eventually getting near-perfect accuracy. This looks great until you realize it's memorizing noise instead of learning patterns.

Error on the test set will tell you how good your model really is.

Initially, as you add complexity, test error decreases because the model starts capturing real patterns. But past a certain point, test error increases even though training error keeps dropping. The model is overfitting - learning quirks specific to the training set that don't generalize.

A small gap between train and test error means your model generalizes well. A large gap means you're overfitting and need to reduce complexity or add more training data.

Techniques to Manage the Bias-Variance Tradeoff

You can't eliminate the bias-variance tradeoff, but you can control it with the right techniques. Let me show you a few.

Train/test splits

Never evaluate your model on the same data you trained it on.

Split your data into training and test sets before you do anything else. Train on one portion, evaluate on the other. This gives you an honest measure of how well your model generalizes to new data.

The test set acts as a proxy for real-world performance. When training error is low but test error is high, you know you're overfitting. When both are high, you're underfitting.

Cross-validation

Train/test splits have a weakness - they depend on which specific examples end up in each set.

Cross-validation fixes this by training and testing multiple times on different splits of your data. The most common approach is k-fold cross-validation, where you divide your data into k parts, train on k-1 parts, and test on the remaining part. Repeat k times so each part serves as the test set once.

This gives you a more reliable estimate of model performance and helps you tune hyperparameters without overfitting to a single test set.

Regularization

Regularization adds a penalty for model complexity directly into your loss function.

Techniques like L1 (Lasso) and L2 (Ridge) regularization discourage large parameter values, which forces the model to stay simpler and more stable. This increases bias slightly but reduces variance, often improving overall test performance.

Dropout in neural networks works similarly - it randomly drops neurons during training, which prevents the network from relying too heavily on specific parameters and reduces overfitting.

More data versus better models

More training data is often the best solution to high variance.

When you have more examples, your model sees a broader sample of possible patterns. This makes it harder to overfit to noise because the noise averages out across more data points. The variance decreases without sacrificing the low bias of a complex model.

But collecting more data isn't always practical or possible.

If you're stuck with limited data, focus on model selection instead - pick simpler models, add regularization, or use ensemble methods that combine multiple models to reduce variance.

Feature selection

Not all features improve your model. Some will just add noise.

Remove irrelevant or redundant features to reduce model complexity without losing important patterns. Fewer features mean fewer parameters to learn, which decreases variance. You also avoid the curse of dimensionality where models struggle in high-dimensional spaces with limited data.

Use techniques like correlation analysis, feature importance scores from tree-based models, or regularization methods that automatically zero out unimportant features.

The goal is to find the minimal set of features that captures the signal without the noise.

Common Misconceptions About the Bias-Variance Tradeoff

Let me clear up three common mistakes that lead people to make poor modeling decisions.

"Lower bias is always better"

Wrong. Lower bias means your model can represent complex patterns, but that's only useful if those patterns actually exist in your data and generalize to new examples.

Reducing bias by adding complexity often increases variance faster than it decreases bias. You end up with a model that fits training data perfectly but performs worse on test data. The goal is minimizing total error, not just bias.

Sometimes a simpler model with higher bias performs better overall because it has low enough variance to generalize well.

"Overfitting means the model is bad"

Not exactly. Overfitting means your model is too complex for the amount of data you have, but the model itself isn't inherently bad.

The same neural network architecture that overfits on 1,000 training examples might perform perfectly on 100,000 examples. The problem is in the mismatch between capacity and data size.

You can fix overfitting by adding more data, reducing complexity, or applying regularization. You don't need to throw away the model and start over with something completely different.

"More data always fixes variance"

More data reduces variance, but it doesn't eliminate it, and there are limits to how much it helps.

If your model is extremely complex relative to your problem, even large datasets might not stabilize it enough. A neural network with millions of parameters needs massive amounts of data to train well.

Also, adding more data only helps if the new data represents the same distribution as your test data. Collecting more biased or noisy data won't reduce variance - it might even make things worse by reinforcing patterns that don't generalize.

Bias-Variance Tradeoff vs. Overfitting and Underfitting

Bias-variance and overfitting-underfitting describe the same problems from different angles, but they're not interchangeable terms.

Here’s what you need to remember:

• High bias causes underfitting. When your model has strong assumptions that don't match real data, it systematically misses patterns in both training and test data. The model is too simple to represent the true relationship, which is what underfitting means.
• High variance causes overfitting. When your model is too sensitive to training data, it learns noise and patterns that don't generalize. The model memorizes training examples instead of learning the underlying pattern, which is what overfitting means.

Bias and variance are properties of your model.

They describe how your model behaves across different training sets. You can measure bias by looking at how far your model's average predictions are from the truth. You can measure variance by looking at how much predictions change with different training data.

Underfitting and overfitting are symptoms you observe.

They describe what happens when you train and test your model. You see underfitting when both training and test errors are high. You see overfitting when training error is low but test error is high.

The connection is direct but not one-to-one. High bias usually leads to underfitting, and high variance usually leads to overfitting. But you can have a model with moderate bias and moderate variance that neither underfits nor overfits - it just performs poorly for other reasons, like wrong features or insufficient data quality.

Practical Tips for Interpreting Model Performance

Here are some last minute tips on how to diagnose bias-variance issues and make better modeling decisions.

Look at training and validation errors together, not separately

Training error alone tells you nothing about generalization. A model with 1% training error could have 50% test error if it's overfitting.

Compare the two errors to understand what's happening.

• When both are high, you have high bias - the model is too simple
• When training error is low but validation error is high, you have high variance - the model is overfitting
• When both are low, you've found the right balance

Don't optimize for training accuracy alone

Perfect training accuracy is a red flag. It usually means you've memorized the training set without learning patterns that generalize.

Focus on validation performance instead. Your goal is minimizing the gap between training and validation error while keeping both reasonably low.

Use cross-validation to get reliable estimates

A single train-test split can be misleading because it depends on which examples ended up in each set. One unlucky split might make a good model look bad or a bad model look good.

Cross-validation averages performance across multiple splits, which gives you a more stable estimate of how your model will perform on new data. This is especially important when you have limited data or when you're tuning hyperparameters.

Balance simplicity and flexibility based on your data size

With small datasets, bias toward simpler models. They're more stable and less likely to overfit when you don't have many examples to learn from.

With large datasets, you can afford more complex models because the extra data stabilizes the learning process and reduces variance. But don't add complexity just because you can - only add it if it improves validation performance.

Conclusion

You can't build a model with zero bias and zero variance. Every modeling decision you make changes the balance between these two error sources. Add complexity and you reduce bias but increase variance. Simplify and you reduce variance but increase bias.

Model performance depends on finding the right balance. The best model is the one that minimizes total error by balancing bias and variance for your specific problem and dataset. Understanding this tradeoff means you can diagnose whether your model suffers from high bias or high variance and apply the right solution.

If you’re ready to get hands-on experience with machine learning, enroll in our Machine Learning Fundamentals in Python track. It has 16 hours of video materials that will help you land your first job.