Chi-Square Test in R: A Complete Guide

Understanding how to analyze and interpret data is an invaluable skill for data professionals. There are many different statistical tests that are used for different reasons. The chi-square test is a common test that is used in a specific context: when you need to determine associations between categorical variables. This is a common thing researchers need to know, which is why the chi square test is one of the most widely used statistical tests.

This tutorial introduces the chi-square test, its different types, and the steps to perform it using the R programming language. By the end of this guide, you’ll be equipped with the knowledge and skills to confidently apply the chi-square test to your own data and interpret the results.

If you’re new to the R programming language, you may want to check out the beginner-friendly Data Analyst with R career track to familiarize yourself with the language through hands-on data analysis examples.

Main Steps: How to Perform a Chi-Square Test in R

To perform a chi-square test in R, follow these steps:

• Step 1: Prepare your data in a contingency table format.

• Step 2: Use the chisq.test() function to apply the chi-square test.

Here is a quick example demonstrating it using sample data:

# Step 1: Creating a contingency table
data <- matrix(c(10, 20, 30, 40), nrow = 2)

# Step 2: Applying the chi-square test function
result <- chisq.test(data)

# Viewing the result
print(result)

This code snippet creates a 2x2 contingency table and performs the chi-square test. The result will show the test statistic, degrees of freedom, and p-value.

What is a Chi-Square Test?

A chi-square test is a statistical test used to determine if there is a significant association between categorical variables. It compares the observed frequencies of occurrences in different categories with the frequencies expected if there were no associations between the variables.

Types of chi-square tests

There are two main types of chi-square tests:

1. Chi-Square Test of Independence: It helps determine whether the variables are independent or if there’s a relationship between them. For example, you might want to know if gender affects voting preference.
2. Chi-Square Test of Goodness of Fit: This test checks if the sample data fits a population distribution. For example, you might want to see if a die is fair by comparing the observed frequency of each face with the expected frequency if the die were fair.

Assumptions of the chi-square test

To ensure the validity of the chi-square test, certain assumptions must be met:

• The data must be in the form of frequencies or counts of cases.
• The categories should be mutually exclusive.
• For the chi-square test of independence, the expected frequency in each category should be at least 5.
• The goodness of fit test expects a frequency of at least 1, with no more than 20% of expected frequencies being less than 5.

Practical applications of chi-square tests

Chi-square tests are widely used in academia and industry, especially for testing hypotheses about the independence of categorical variables. Some of these practical applications are:

• Market Research: Some applications include analyzing if customer preferences for a product vary across different age groups and income levels or determining if different marketing campaigns are equally effective across demographic segments.
• Medical Research: Common use cases are studying the association between lifestyle factors (e.g., smoking, exercise) and the incidence of diseases (e.g., lung cancer, heart disease) or evaluating whether different treatment groups show different recovery rates in clinical trials.
• Quality Control: Commonly used to examine whether product defects are independent of the manufacturing process or specific production lines and to compare the quality of products from different suppliers to determine if there is a significant difference in defect rates.
• Education: The tests are often used to determine if there is a significant difference in pass rates between students from different schools or teaching methods and to evaluate if introducing a new curriculum improves student performance across subjects.

It’s worth noting that these are some of the many applications across academia and the industry and can be extended to other domains and fields.

Performing a Chi-Square Test in R: An Example

The best way to learn to perform chi-square tests is through an example where we apply the test to a dataset. We’ll use the Anemia Levels in Nigeria dataset, which can be downloaded from Kaggle. The dataset comes from the 2018 Nigeria Demographic and Health Surveys (NDHS). It explores the impact of mothers’ age and socioeconomic factors on anemia levels among children aged 0–59 months across Nigeria’s 36 states and the Federal Capital Territory. 

Let’s load the dataset in R and examine a sample to understand the data better. To read CSV files in R, you’ll need to install a package called readr.

# Load the necessary libraries
install.packages('readr')
library(readr)

# Load the dataset from the CSV file
dataset <- read_csv("children anemia.csv")

# Display the first few rows of the dataset
head(dataset)

# Rename a column
colnames(dataset)[colnames(dataset) == "Anemia level...8"] <- "Anemia level"

# Display the column names
colnames(dataset)

In addition to a sample of the dataset, we’ll see the columns of the dataset below:

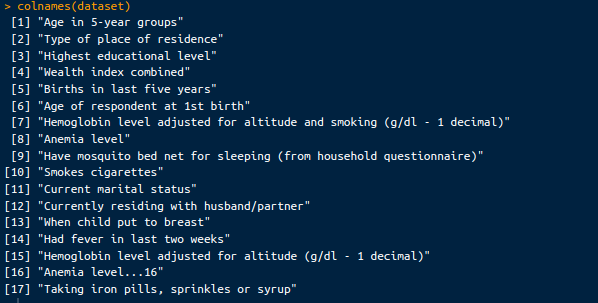Columns in the dataset. Image by Author.

Among them, we’ll pick these two columns to evaluate if there is a relationship between them.

• Highest educational level: This column categorizes the mother’s education into “No education,” “Primary,” “Secondary,” and “Higher” levels.

• Anemia level: This column indicates the anemia level of the child, such as “Moderate,” “Severe,” or “No Anemia.”

Step 1: Creating a contingency table

A contingency table, also known as a cross-tabulation or cross-tab, shows how the values of two or more categorical variables are distributed across their respective categories. 

We’ll select the two selected columns from the dataset and convert them to the required contingency table format. We’ll use a commonly used package called dplyr for these operations.

# Install and load the package
install.packages('dplyr')

library(dplyr)

# Select the columns of interest
selected_data <- dataset %>% select(Highest educational level, Anemia level)

# Create a contingency table for Highest educational level and Anemia level
contingency_table <- table(selected_data$Highest educational level, selected_data$Anemia level)

# View the contingency table
print(contingency_table)

The resulting contingency table looks like this:

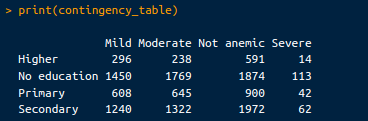
Contingency table. Image by Author.

Step 2: Applying the chi-square test function

Since we have the dataset in the contingency table format we want, we can simply apply the chisq.test() function. No libraries need to be loaded to call this function, as it’s available in the base R package.

# Perform chi-square test
chi_square_test <- chisq.test(contingency_table)

# View the results
print(chi_square_test)

The output will look like:

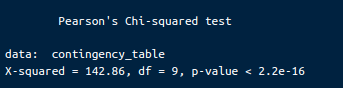
Pearson’s chi-square test results. Image by Author.

That’s it! We have performed the chi-square test in two simple steps. Next, how do we interpret the results?

Formulating Hypothesis & Interpreting the Results

Hypotheses clearly state what we are testing and establish a framework for interpreting the results. In simpler terms, the hypothesis we formulate gives us a clear question to answer, and the chi-square test helps us determine whether the observed data supports or refutes the claim.

Hypotheses for the chi-square test

When performing a chi-square test, we typically establish two hypotheses:

• Null Hypothesis (H0): The null hypothesis states that there is no association between the two categorical variables being tested. It assumes that any observed differences in the data are due to random chance rather than a true relationship.
• Alternative Hypothesis (H1): The alternative hypothesis states that there is a significant association between the two variables. It suggests that the observed differences are not due to random chance and that there is a relationship between the variables.

Applying the concepts of null and alternative hypothesis to the variables we have performed the chi-square test on, we can formulate the hypothesis as:

• Null Hypothesis (H0): The null hypothesis is that there is no association between the mother’s highest educational level and the child’s anemia level. This means we assume that the likelihood of a child having anemia is independent of the mother’s education level.
• Alternative Hypothesis (H1): The alternative hypothesis is that there is an association between the mother’s highest educational level and the child’s anemia level. This implies that the mother’s education level affects the likelihood of the child having anemia.

Interpreting the output of the chi-square test

Now that we’ve formed a hypothesis, we can interpret the results in the context of the hypothesis:

• Chi-Square Statistic (X-squared): The chi-square test statistic is 142.86. This value measures the discrepancy between the observed frequencies in the contingency table and the frequencies we would expect if there were no associations between the variables.

• Degrees of Freedom (df): The degree of freedom for this test is 9. This is calculated as (number of row - 1) * (number of columns - 1).

• P-Value: The p-value is less than 2.2e-16, which is extremely small. This p-value indicates the probability of observing a chi-square statistic as extreme as, or more extreme than, 142.86 if the null hypothesis were true.

We reject the null hypothesis since the p-value is much smaller than common significance levels (e.g., 0.05, 0.01, or even 0.001). This provides strong evidence of a significant association between the mother’s education level and the child’s anemia status. In other words, the chi-square test results indicate that the likelihood of a child having anemia is significantly associated with the mother’s level of education.

Additional Analysis: Accessing Values from chisq.test()

Beyond hypothesis testing, we can retrieve certain values from the object returned by the chisq.test() function:

Observed counts

These represent the actual counts of children with different anemia levels across each mother’s education level. The observed counts can be retrieved from the following code:

# Observed counts
observed_counts <- chi_square_test$observed

print(observed_counts)

The output is as follows:

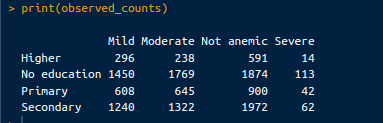
Observed counts. Image by Author.

Expected counts

These counts are calculated under the assumption that there is no association between the mother’s education level and the child’s anemia status. The expected counts can be retrieved from the following code:

# Expected counts
expected_counts <- chi_square_test$expected
print(round(expected_counts, 2))

The output is as follows:

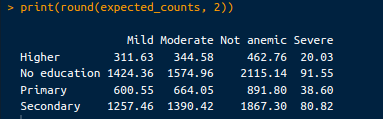
Expected counts. Image by Author.

Pearson residuals

These residuals help identify the largest discrepancies between observed and expected counts, indicating which cells contribute most to the chi-square statistic. The Pearson residuals can be retrieved from the following code:

# Pearson residuals
pearson_residuals <- chi_square_test$residuals
print(round(pearson_residuals, 2))

The output is as follows:

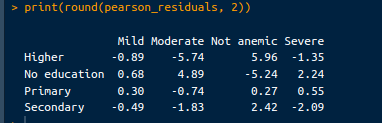
Residuals output. Image by Author.

Let us try to understand what these residual numbers mean:

• Positive Residuals: Positive residuals indicate that the observed count is higher than expected. For example, a residual of 5.96 for "Not anemic" in the "Higher" education group means that there are significantly more children who are not anemic than expected among mothers with higher education.

• Negative Residuals: Negative residuals indicate that the observed count is lower than expected. For instance, a residual of -5.74 for "Moderate" anemia in the "Higher" education group suggests that there are significantly fewer moderately anemic children than expected among mothers with higher education.

• Large Residuals: Large positive or negative residuals suggest a significant deviation from what was expected. These cells contribute most to the chi-square statistic. For example, the large positive residual for “Not anemic” in the “Higher” education group and the large negative residual for “Moderate” anemia in the same group indicate strong deviations in the anemia levels of children based on the mother’s education level.

• Small Residuals: Small residuals (close to 0) suggest that the observed counts are close to the expected counts, indicating a weaker deviation. For example, the residuals for “Primary” education across the anemia levels are relatively smaller, indicating that the observed and expected counts are closer for this group.

Contribution diagram

Based on the values extracted above, the contribution of each cell to the chi-square statistic can be calculated by the code below and converted into a percentage:

# Calculate contribution to chi-square statistic
contributions <- (observed_counts - expected_counts)^2 / expected_counts

# Calculate percentage contributions
total_chi_square <- chi_square_test$statistic
percentage_contributions <- 100 * contributions / total_chi_square

# Print percentage contributions
print("Percentage Contributions:")
print(round(percentage_contributions, 2))

The output we’ll see is as follows:

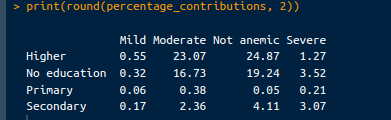Percentage contributions. Image by Author.

The calculated contribution can be visualized as a heatmap. We will use a package called pheatmap to do so, after installing and loading the package.

# Install and load heatmap package
install.packages("pheatmap")
library(heatmap)

# Create heatmap for percentage contributions
pheatmap(percentage_contributions,
        display_numbers = TRUE,
        cluster_rows = FALSE,
        cluster_cols = FALSE,
        main = "Percentage Contribution to Chi-Square Statistic")

The resulting output is as follows:

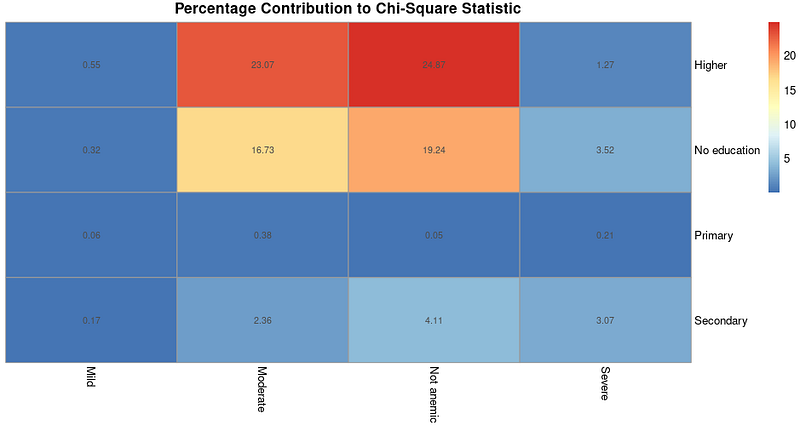Percentage contribution to chi-square statistic heatmap. Image by Author.

A heatmap like the one above with contributions can be useful if you choose to perform further analysis to understand what type of associations exist after we find out associations exist based on the chi-square test results.

Conclusion

This tutorial introduced you to the chi-square test, its different types, and the underlying assumptions. We further learned how to perform the test and interpret the results in R with added visualization using an example. 

Chi-square tests are commonly used during hypothesis testing and generally in statistics. Consider taking up one of these courses to solidify your understanding of data analytics and statistics using R:

• Introduction to Statistics in R course
• Exploratory Data Analysis in R course
• Hypothesis Testing in R course