Course
"Cosine distance." Image by Dall-E.
Measuring the similarity or dissimilarity between data points is helpful for many applications, from text analysis to recommendation systems. Cosine distance is one distance metric that is particularly effective for high-dimensional data or sparse datasets, as it focuses on vector orientation rather than magnitude.
If you would like a refresher on the common and important concepts in machine learning, start with our comprehensive tutorial, Demystifying Mathematical Concepts for Deep Learning. Consider also reading another article on distance-based learning, What is Manhattan Distance? to broaden your understanding of distance metrics and see the differences between cosine distance and Manhattan distance.
Defining Cosine Distance
Let's now take some time to define cosine distance according to the cosine distance formula. To do so, we also consider its relationship to cosine similarity.
Cosine distance formula
Cosine distance measures the dissimilarity between two vectors by calculating the cosine of the angle between them. It can be defined as one minus cosine similarity, as we see in the formula below:
![]()
In a more detailed way, with a more formal mathematical expression, cosine distance is calculated using the formula below.
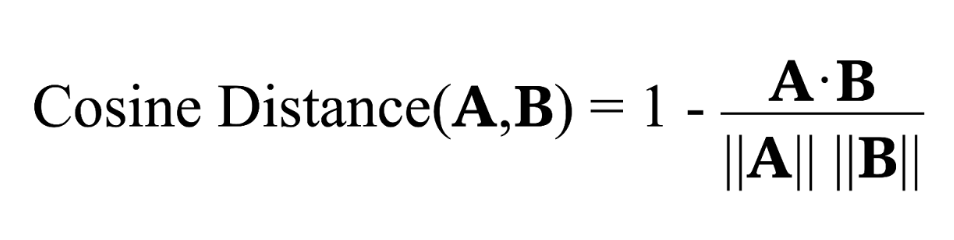
Here, A⋅B represents the dot product of the vectors A and B, and ||A|| ||B|| are the magnitudes, or Euclidean norms, of the vectors.
With this formula we are quantifying cosine distance with a range from 0 to 2. A cosine distance of 0 means the vectors are perfectly aligned (no angle between them), indicating maximum similarity, while a value closer to 2 suggests they are diametrically opposite, indicating maximum dissimilarity.
Cosine similarity vs. cosine distance
As we have seen, while cosine distance measures the dissimilarity between vectors by calculating the cosine of the angle between them, cosine similarity quantifies how similar two vectors are based on the cosine of the same angle.
Cosine similarity ranges from -1 to 1. A cosine similarity of 1 means the vectors are perfectly aligned (no angle between them), indicating maximum similarity, whereas a value of -1 implies they are diametrically opposite, reflecting maximum dissimilarity. Values near zero indicate orthogonality.
Calculating and Visualizing Cosine Distance
Let’s take an example with two vectors: Vector A (2,4) and Vector B (4,2), and calculate their cosine distance by following these steps:
- Calculate the dot product of A and B:
A · B = (2 × 4) + (4 × 2) = 8 + 8 = 16 - Calculate the magnitudes of A and B:
||A|| = √(2² + 4²) = √20
||B|| = √(4² + 2²) = √20
- Divide the dot product by the product of the magnitudes:
(A · B) / (||A|| × ||B||) = 16 / (√20 × √20) = 16 / 20 = 0.8
- Calculate the cosine distance:
Cosine Distance = 1 - 0.8 = 0.2
With a cosine distance of 0.2, the result falls quite low on the 0 to 2 scale. This suggests that vectors A and B are quite similar in terms of the direction they point to.
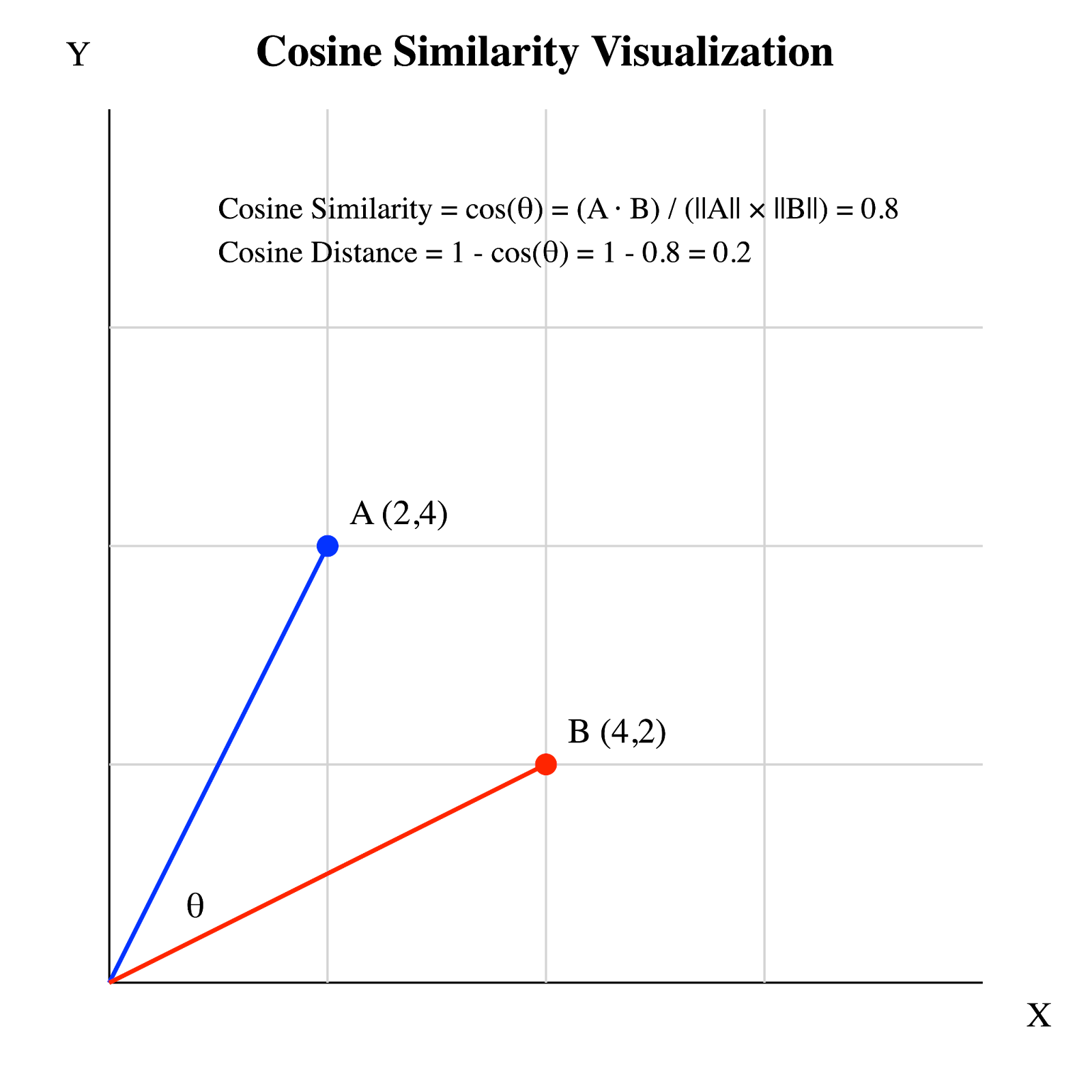 Cosine distance and cosine similarity. Image by Author.
Cosine distance and cosine similarity. Image by Author.
In this representation:
- Vector A is (2, 4)
- Vector B is (4, 2)
- θ is the angle between A and B
The cosine similarity (0.8) represents the cosine of angle θ. As the vectors are close in direction, the angle is small, resulting in a high cosine similarity and a low cosine distance (0.2).
Because cosine distance can also be defined as 1 - cos(θ), where cos(θ) is the cosine similarity, this implies:
- When vectors are identical in direction (θ = 0°), cos(θ) = 1, so cosine distance = 0
- When vectors are perpendicular (θ = 90°), cos(θ) = 0, so cosine distance = 1
- When vectors are opposite (θ = 180°), cos(θ) = -1, so cosine distance = 2
Applications of Cosine Distance
Let’s take a look at some of the important applications.
Natural language processing (NLP)
Cosine distance plays a crucial role in various natural language processing tasks by effectively measuring semantic relationships between text representations such as word2vec. For a brief overview of these concepts, you may find our tutorial on Understanding Text Classification in Python useful.
Document classification and similarity
In document classification, cosine distance measures content similarity by comparing the angles between document vectors. Each document is converted into a vector, with dimensions reflecting TF-IDF scores of words. Similar documents point in similar directions, resulting in smaller cosine distances.
Clustering and semantic grouping
Cosine distance excels in clustering tasks like K-means clustering, grouping semantically related documents even if they don't use the same words. It's ideal for high-dimensional, sparse data common in text processing. By capturing vector orientation, it enables more accurate thematic clustering. This technique is often used in unsupervised learning to discover natural groupings within document sets, such as grouping news articles by topics.
Information retrieval and search engines
In information retrieval, cosine distance matches search queries to documents by vector comparison. Search engines then find documents closest to the query vector in terms of cosine distance, ranking those with the smallest distances highest for relevance.
Word embeddings and word similarity
Beyond document-level analysis, cosine distance is vital in word embeddings like Word2Vec or GloVe, where words are represented as high-dimensional vectors. These embeddings capture semantic meaning such that words with similar meanings are embedded close together in the vector space. Cosine distance can be used to find the most similar words to a given word, support synonym detection, or even power features in more complex models like those used for sentiment analysis or machine translation.
Image recognition
In image recognition, cosine distance steps in to compare feature vectors extracted from images. Whether it's sorting out faces in a crowd or classifying nature photos, it looks at how similar the vectors are in orientation, not just size. This focus helps in nailing down the right categories for images, boosting both the accuracy and effectiveness of image-based systems.
Recommender systems
Imagine cosine distance as a matchmaker in the digital world, pairing users with movies or products that align with their past likes. By looking at how closely user and item profiles align in their vector spaces, recommendation systems predicts what you'll probably enjoy next with surprising accuracy.
Mathematical Properties of Cosine Distance
Cosine distance has unique mathematical properties that differentiate it from other distance measures. Understanding these properties is important for correctly interpreting and applying cosine distance in different contexts.
Metric space properties
In mathematics, a metric or distance function is a function that defines the distance between each pair of elements in a set. To be considered a true metric, a function must satisfy four conditions:
-
Non-negativity: d(x, y) ≥ 0
-
Identity of indiscernibles: d(x, y) = 0 if and only if x = y
-
Symmetry: d(x, y) = d(y, x)
-
Triangle inequality: d(x, z) ≤ d(x, y) + d(y, z)
Cosine distance satisfies the first three conditions but does not always satisfy the triangle inequality. This means that in some cases, the sum of the cosine distances between points A and B and between B and C might be less than the cosine distance between A and C.
Scale invariance
One notable property of cosine distance is its scale invariance. This means that the cosine distance between two vectors remains the same even if you multiply either or both vectors by a scalar (non-zero constant). Mathematically, for any nonzero scalars a and b, and vectors x and y:
Cosine Distance(ax, by) = Cosine Distance(x, y)
This property of scale invariance distinguishes cosine distance from many other distance measures.
Cosine Distance in Python and R
Here, we'll explore how to calculate cosine distance using Python and R.
Python example
In Python, we can use NumPy to calculate cosine distance and cosine similarity. We do this by finding the dot product and the norm of our vectors.
import numpy as np
# Define the vectors
A = np.array([2, 4])
B = np.array([4, 2])
# Calculate cosine similarity
cos_similarity = np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
# Calculate cosine distance
cos_distance = 1 - cos_similarity
print("Cosine Similarity: {:.2f}".format(cos_similarity))
print("Cosine Distance: {:.2f}".format(cos_distance))Output:
Cosine Similarity: 0.80
Cosine Distance: 0.20Alternatively, we could find cosine distance using the SciPy package and the cosine() function.
import numpy as np
from scipy.spatial.distance import cosine
# Define the vectors
A = np.array([2, 4])
B = np.array([4, 2])
# Calculate cosine distance
cos_distance = cosine(A, B) # Uses scipy's cosine for cosine distance
print("Cosine Distance: {:.2f}".format(cos_distance))Output:
Cosine Distance: 0.20R example
In R, you can calculate cosine similarity and cosine distance using basic vector operations. Here’s how:
# Define the vectors
A <- c(2, 4)
B <- c(4, 2)
# Calculate cosine similarity
cos_similarity <- sum(A * B) / (sqrt(sum(A^2)) * sqrt(sum(B^2)))
# Note: We can also use %*% operator for matrix multiplication.
# %*%, when applied to two vectors, calculates the dot product.
# For example: cos_similarity <- A %*% B / (sqrt(sum(A^2)) * sqrt(sum(B^2)))
# Calculate cosine distance
cos_distance <- 1 - cos_similarity
# Print the result
print(paste("Cosine Similarity:", cos_similarity))
print(paste("Cosine Distance:", cos_distance))Output:
“Cosine Similarity: 0.80”
“Cosine Distance: 0.20”In the R example, the cosine similarity is calculated using manual operations for dot product and norms, similar to the Python example, but entirely within R's base functionality. Notice how the cosine distance is derived by subtracting the cosine similarity from 1.
Cosine Similarity vs. Euclidean Distance and Other Distance Metrics
The visual below expands on our original example, but this time, it uses different colors to represent three types of distance measurements using the same vectors:
- Manhattan Distance measures the sum of the absolute differences of their coordinates.
- Euclidean Distance calculates the straight-line distance between two points.
- Cosine Distance is derived from the cosine of the angle between two vectors.
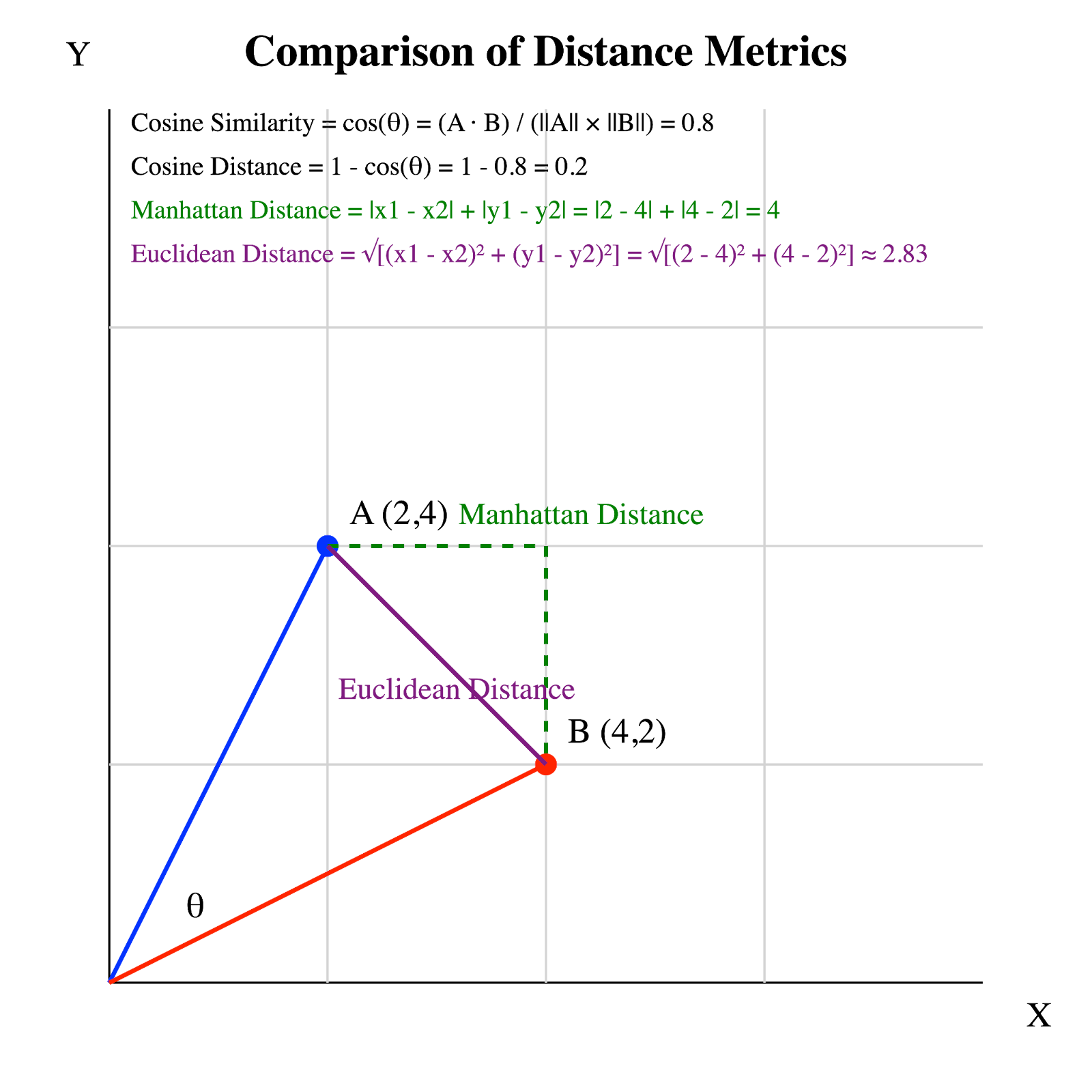
Cosine distance vs. Euclidean distance vs. Manhattan distance. Image by Author.
Each of these distances provides unique insights into data. Euclidean and Manhattan distances are geometric distances that take into account the magnitude of the vector components, which makes them suitable for physical measurements in space. Cosine distance, in contrast, focuses on the angle between vectors, making it ideal for understanding orientation and directionality, especially in high-dimensional spaces like those used in text analysis and other forms of data science.
Conclusion
Cosine distance and its complement, cosine similarity, are powerful tools in data science and machine learning. These metrics offer unique insights into the relationships between vectors, particularly in high-dimensional spaces where traditional distance measures may fall short.
As data continues to grow in complexity and dimensionality, metrics like cosine distance will likely play an increasingly important role in uncovering hidden patterns and relationships. Whether you're working on natural language processing, recommendation systems, or any field dealing with high-dimensional vector spaces, understanding and applying cosine distance can provide valuable insights and improve the performance of your models. As a next step, take our comprehensive interactive course, Designing Machine Learning Workflows in Python, which has a whole chapter on distance-based learning and unsupervised workflows.
As an adept professional in Data Science, Machine Learning, and Generative AI, Vinod dedicates himself to sharing knowledge and empowering aspiring data scientists to succeed in this dynamic field.
Frequently Asked Questions
What is cosine similarity?
Cosine similarity is a metric used to measure how similar two vectors are in their orientation, irrespective of their magnitude.
What is the range of cosine similarity?
The range of cosine similarity is -1 to 1
What is the cosine similarity formula?
The cosine similarity formula calculates the cosine of the angle between two vectors, defined as the dot product of the vectors divided by the product of their magnitudes.
What is the dot product vs cosine similarity?
The dot product is the sum of the products of corresponding elements of two vectors, reflecting both their magnitude and orientation. Cosine similarity, on the other hand, is the dot product normalized by the product of the vectors' magnitudes, focusing solely on their directional alignment.
How does cosine distance differ from cosine similarity?
Cosine distance and cosine similarity are complementary measures. Cosine similarity measures how similar two vectors are, ranging from -1 (exactly opposite) to 1 (exactly the same). Cosine distance, on the other hand, measures how different two vectors are and is calculated as 1 minus the Cosine Similarity. It ranges from 0 (identical vectors) to 2 (opposite vectors).
What is the cosine distance formula?
The cosine distance formula measures the angle between two vectors in a multi-dimensional space, calculated as 1 minus the cosine of the angle between the vectors.
What does a cosine distance of 1 indicate?
A cosine distance of 1 indicates that the two vectors being compared are perpendicular (orthogonal) to each other, forming a 90-degree angle. This means the vectors have no directional similarity, which in practical terms suggests completely different themes in text analysis, unrelated items in recommendation systems, or distinct characteristics in machine learning feature vectors.
What's the difference between cosine distance and angular distance?
Cosine distance and angular distance are closely related but not identical. Cosine distance is defined as 1 minus the cosine similarity, while angular distance is the angle between two vectors in radians, calculated as the arccosine of the cosine similarity. Angular distance is proportional to cosine distance but provides a more intuitive geometric interpretation.
What's the difference between cosine distance and Euclidean distance?
While both measure dissimilarity, cosine distance focuses on the angle between vectors, ignoring magnitude. Euclidean distance focuses on magnitude, measuring the straight-line distance between two points in space.
Why is cosine distance useful in text analysis?
Cosine distance is particularly useful in text analysis because it focuses on the proportion of words (represented as vector dimensions) rather than their absolute frequencies. This makes it effective for comparing documents of different lengths and for identifying thematic similarities regardless of document size.

