Course
Have you ever wondered why your investment portfolio's average price-to-earnings ratio seems unusually high when using a simple average? Or why combining parallel resistors in an electrical circuit requires a special kind of averaging? These scenarios highlight the importance of understanding the harmonic mean – a powerful statistical tool that's particularly useful when dealing with rates, ratios, and reciprocal relationships.
In this tutorial, we'll explore the harmonic mean, its applications, and why it's sometimes a better choice than other types of averages. We'll see how it's used in various fields, from finance to physics, and its growing importance in data science and machine learning. If you're interested in pursuing a career in this field, our Machine Learning Scientist in Python career track offers comprehensive coverage of these and other essential statistical concepts.
What is the Harmonic Mean?
The harmonic mean is a type of average that's particularly useful when working with rates or ratios. Unlike the arithmetic mean, which simply adds numbers and divides by the count, or the geometric mean, which handles multiplicative relationships, the harmonic mean is designed for situations where you're dealing with reciprocal relationships.
For a set of numbers, the harmonic mean is calculated by:
- Taking the reciprocal of each number.
- Finding the arithmetic mean of these reciprocals.
- Taking the reciprocal of that result.
When to Use the Harmonic Mean
The harmonic mean is useful in several scenarios across different fields. I hinted at these in the introduction, but let's look in detail at each domain where this statistical measure proves particularly valuable.
Financial analysis
In finance, the harmonic mean calculates accurate portfolio metrics. It's particularly useful for working with price-to-earnings (P/E) ratios, where it provides a more accurate representation of portfolio valuation than simple averages. Financial analysts also rely on it for various other financial ratios and rates, as well as for cost averaging in dynamic pricing scenarios where rates fluctuate over time.
Physics and engineering
Engineers and physicists frequently employ the harmonic mean in their calculations. It's often used when calculating the total resistance of parallel circuits, where individual resistors are combined. In acoustics, it helps analyze sound wave frequencies, and in optics, it's used for combinations of lenses where reciprocal relationships are common.
Data science
The data science field heavily utilizes the harmonic mean, particularly in machine learning applications. It's the foundation of the F1-score, which balances precision and recall in classification problems. Data scientists also use it for evaluating performance metrics in imbalanced datasets and in collaborative filtering systems for recommendation engines, where different types of similarity measures need to be combined.
General applications
Beyond specialized fields, the harmonic mean finds use in everyday calculations. It's the correct choice for calculating average speeds over fixed distances, determining production rates in manufacturing processes, and measuring network data transfer rates where reciprocal relationships are involved. In these cases, the harmonic mean provides more accurate results than simple arithmetic averages.
How to Calculate the Harmonic Mean
Let's break down the calculation process with clear steps and examples.
The harmonic mean formula
The harmonic mean (H) of n numbers is calculated as:
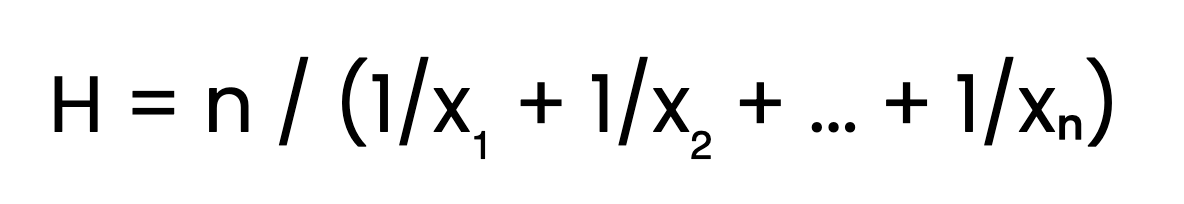
Where x₁, x₂, ..., xₙ are the values in your dataset.
Step-by-step example
Let's calculate the harmonic mean of three numbers: 2, 4, and 8.
- Take the reciprocal of each number: 1/2 = 0.5. 1/4 = 0.25. 1/8 = 0.125
- Add these reciprocals: 0.5 + 0.25 + 0.125 = 0.875
- Divide the count (3) by this sum: 3 / 0.875 = 3.429
The harmonic mean of 2, 4, and 8 is approximately 3.429.
Weighted Harmonic Mean
Sometimes not all values should have equal importance in your calculation. The weighted harmonic mean addresses this by allowing you to assign different weights to different values.
Weighted harmonic mean formula
For values x₁, x₂, ..., xₙ with corresponding weights w₁, w₂, ..., wₙ:
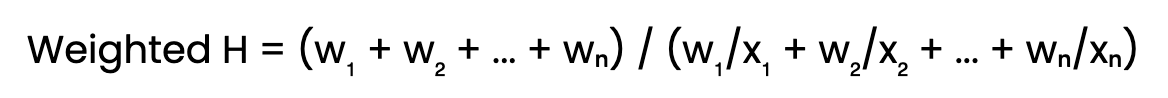
This is particularly useful in:
- Portfolio analysis where investments have different sizes
- Quality metrics where some measures are more important than others
- Customer satisfaction scores where some factors carry more weight
Harmonic Mean in Data Science and Machine Learning
The harmonic mean has found numerous applications in modern data science and machine learning.
F1-score calculation
The F1-score, as I mentioned, is a popular metric in machine learning. It is the harmonic mean of precision and recall:

This ensures that both precision and recall must be reasonably high for a good F1-score, as the harmonic mean penalizes extreme imbalances between the two metrics. To better understand how to visualize and interpret these metrics, check out our detailed Precision-Recall Curve in Python tutorial, which provides hands-on examples and practical implementations.
Cross-validation
When evaluating model performance across different folds:
- The harmonic mean of performance metrics ensures poor performance in any fold is properly weighted.
- It's particularly useful when working with imbalanced datasets.
- Helps identify models that perform consistently across different data splits.
For a comprehensive study on validation techniques, you can explore our Guide to K-Fold Cross Validation, which covers advanced strategies for robust model evaluation.
Recommendation systems
In collaborative filtering and recommendation systems, the harmonic mean can be used to create balanced, user-friendly suggestions. When building recommender systems, data scientists often need to combine different similarity metrics - such as user behavior patterns, item characteristics, and historical interactions. The harmonic mean helps balance these metrics by ensuring that recommendations aren't overly influenced by any single factor.
For example, when weighing user preferences, a movie recommendation system might need to balance a user's genre preferences with their rating history and viewing duration patterns. The harmonic mean also helps solve the "diversity-relevance tradeoff" by preventing recommendations from becoming too narrow or too scattered. This is particularly valuable in e-commerce and content streaming platforms, where maintaining user engagement requires a delicate balance between suggesting similar items and introducing novel options.
Harmonic Mean vs. Other Means
Let’s take a look at how harmonic mean compares to other types of means and a few scenarios where each can be used.
| Comparison | Arithmetic Mean | Harmonic Mean | Geometric Mean |
|---|---|---|---|
| Best Use Case | Simple average, best for additive relationships | Best for rates and ratios | Best for growth rates and ratios |
| Example | Average daily temperature | Average cost per unit | Investment returns over time |
| Key Limitation | Can misrepresent data with high variability | Cannot be used when any value in the dataset is zero | Cannot handle negative or zero values in the dataset |
| Data Distribution Suitability | Best for normally distributed data | Best for datasets with inverse proportionality | Best for log-normal or skewed data |
For a more in-depth understanding of how other means work, I have tutorials on arithmetic mean and geometric mean.
Key Considerations for Using the Harmonic Mean
Example: Handling extreme values
Consider a fund manager analyzing three stocks with equal investment amounts but dramatically different earnings:
- Stock A: Investment $100, Earnings $2, P/E ratio = 50 (high valuation)
- Stock B: Investment $100, Earnings $10, P/E ratio = 10 (moderate valuation)
- Stock C: Investment $100, Earnings $25, P/E ratio = 4 (low valuation)
Let's compare how different means handle these widely varying P/E ratios:
- Arithmetic Mean: (50 + 10 + 4) / 3 ≈ 21.33 P/E
- Harmonic Mean: 3 / (1/50 + 1/10 + 1/4) ≈ 8.11 P/
To verify the true portfolio P/E:
- Total Investment: $300 ($100 × 3)
- Total Earnings: $37 ($2 + $10 + $25)
- Actual Portfolio P/E: $300/$37 ≈ 8.11
The arithmetic mean of 21.33 is heavily skewed by the extreme P/E ratio of Stock A (50), suggesting a much higher average valuation than reality. The harmonic mean of approximately 8.11 provides the correct portfolio P/E ratio, as it naturally gives less weight to the extreme high value and better represents the true earning power of the combined investments.
Advantages of the harmonic mean
- Ideal for rate-based calculations
- Less sensitive to large outliers
- Provides accurate averages for reciprocal relationships
Limitations of the harmonic mean
- Cannot handle zero values
- More sensitive to small values
- May not be intuitive for non-technical audiences
Conclusion: Why the Harmonic Mean Matters
The harmonic mean is an essential tool and particularly valuable when working with rates, ratios, and reciprocal relationships. While it might not be as commonly used as the arithmetic mean, understanding when and how to apply it can lead to more accurate analyses and better decision-making.
Whether you're evaluating investment portfolios, analyzing machine learning models, or solving physics problems, the harmonic mean provides insights that other averages might miss. By understanding its properties and applications, you can choose the right type of mean for your specific needs and avoid common pitfalls in data analysis. Enroll in our Machine Learning Scientist in Python career track to keep learning.
Become an ML Scientist
As an adept professional in Data Science, Machine Learning, and Generative AI, Vinod dedicates himself to sharing knowledge and empowering aspiring data scientists to succeed in this dynamic field.
Harmonic Mean FAQs
What is the harmonic mean?
The harmonic mean is a type of average that's particularly useful when working with rates and ratios. It's calculated by taking the reciprocal of the arithmetic mean of reciprocals. The harmonic mean is especially valuable when smaller values in your dataset need more emphasis.
How does the harmonic mean differ from the arithmetic mean and geometric mean?
The arithmetic mean is best for adding values directly and the geometric mean works well for growth rates. Unlike other means, the harmonic mean provides the correct result when dealing with rates over equal intervals.
Is the harmonic mean always lower than the arithmetic mean?
Yes, the harmonic mean is always lower than or equal to the arithmetic mean for positive numbers. This relationship, known as the arithmetic-harmonic mean inequality, only reaches equality when all numbers in the dataset are identical. The difference becomes more pronounced as the variation in the dataset increases.
Can the harmonic mean handle zero or negative values?
The harmonic mean cannot handle zero values because it involves division by each value. It also can't handle negative values in its standard form. In such cases, consider using a different measure of central tendency.
How is the weighted harmonic mean different from the regular harmonic mean?
The weighted harmonic mean extends the basic concept by allowing different values to have varying levels of importance. It's particularly useful in portfolio analysis and when some measurements should have more influence than others. The calculation involves dividing the sum of weights by the sum of weighted reciprocals.
Can I calculate the harmonic mean in Excel or other spreadsheet software?
Yes, you can calculate the harmonic mean in Excel using the HARMEAN function, which is built into the software. Most statistical programming languages like Python and R also have built-in functions for calculating the harmonic mean.