Course
The dot product, also known as the scalar product or inner product in Euclidean space, is a fundamental operation in mathematics that combines two vectors to produce a scalar value.
The dot product is very important in several disciplines such as linear algebra, physics, and machine learning. It is so because it facilitates the computation of angles and projections, and consequently calculates similarities between vectors. I would argue that a thorough understanding of the dot product is essential for understanding vector relationships across all these fields.
What Is the Dot Product?
There are different ways to understand and compute dot products; thus, in this section, I will introduce its main definitions and properties.
Algebraic definition
From an algebraic perspective, the dot product of two vectors is computed through a sum of the products of their corresponding components; therefore, for two vectors:
![]()
![]()
The vector product is calculated via:
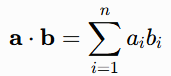
This formulation is computationally straightforward and allows us to generalize dot products to higher dimensions. It is worth noting that the dot product remains invariant under rotations, which underscores its role as an intrinsic measure of vector alignment independent of coordinate choice.
Geometric definition
The geometric interpretation puts the dot product in terms of vector magnitudes and the cosine of the angle θ between them:
![]()
This point of view shows how the dot product quantifies directional relationships and helps formally to understand projections and orthogonality. The equivalence of the algebraic and geometric definitions can be established through the law of cosines.
This point of view shows how the dot product quantifies directional relationships and helps formally to understand projections and orthogonality. The equivalence of the algebraic and geometric definitions can be established through the law of cosines.
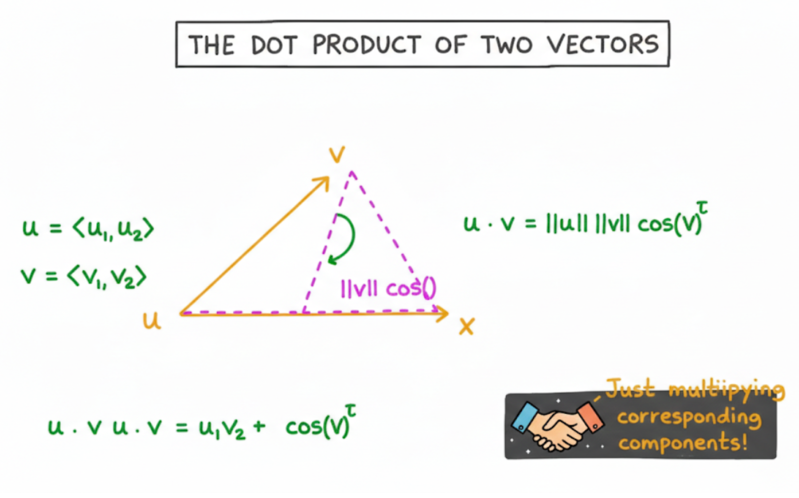
This image illustrates the geometric intuition behind the dot product of two vectors.
It is generally relevant to have a very good intuition of angles and the Pythagorean theorem when dealing with geometry. Thus, don’t hesitate to check out our tutorial on Pythagorean Theorem: Exploring Geometry's Fundamental Relation.
Algebraic properties
The dot product is commutative in nature. This means that taking the dot product of a and b does not change when we swap the order of a and b (a.b = b.a).
The dot product is also distributive over vector addition (a.(b+c) = a.b + a.c). Additionally, it is homogeneous (linear in each argument) and positive-definite, meaning a.a>0 for a not null, which directly supports the definition of the Euclidean norm:
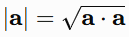
A zero dot product indicates orthogonality, which holds a central significance in many applications. Under the assumption that vectors reside in a real Euclidean space, these properties hold without loss of generality.
Dot product calculation examples
To understand dot product calculation more intuitively, I will show examples of measurement. Consider two 2D vectors a=(1,2) and b=(3,4). Algebraically:
![]()
Geometrically:
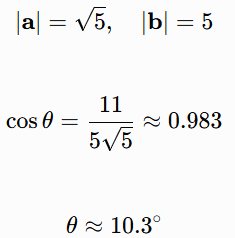
Similarly in 3D, let a=(1,2,3) and b=(4,5,6):
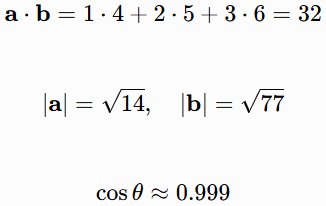
The Dot Product Formula
In this section, I will offer a deeper dive into the geometric formulation for the dot product and understanding its implications.
Vector projection
The scalar projection of b onto a is:
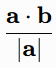
The vector projection is:
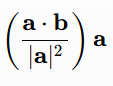
This operation decomposes vectors into parallel and orthogonal components with applications such as shadow casting or force resolution in physics. It is mediated by the dot product and comes from the cosine relationship.
Angles and orthogonality
The dot product, as shown earlier, helps in angle computation via the formula:
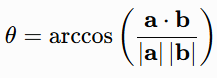
Therefore, when a.b=0, the corresponding main angle would be θ=90°, which offers a tractable method for basis decompositions.
Physical interpretations
In physics, work W done by a constant force F is:
![]()
This formulation extends to power and energy considerations. Projection onto planes also arises in component decomposition and direction cosines.
Properties of the Dot Product
In this section, I will untie the mathematical structure of the dot product as a special case of inner products.
Bilinear forms and inner products
The dot product is a positive-definite bilinear form. In principle, inner products generalize this concept to other space which satisfies symmetry and linearity. The Euclidean dot product, in turn, aligns with the standard inner product in Rn
Complex vectors
For complex vectors, the inner product becomes the Hermitian form:
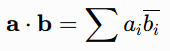
Which is sesquilinear (linear in one argument and conjugate-linear in the other) and thus non-commutative in the usual sense. This modification finds use in quantum mechanics and signal processing.
Important inequalities
The Cauchy-Schwarz inequality states that for every two vectors a and b, the following formula holds:
![]()
With equality when vectors are linearly dependent. This implies the triangle inequality and provides some bounds that are very practical in analysis. Intuitively, it reflects that the projection cannot exceed the magnitude if you try to focus on it thoroughly.
Orthonormal bases
Orthonormal bases simplify dot-product computations to coordinate extractions. They help construct and verify bases in theoretical and practical contexts, such as Fourier analysis.
Dot Product Applications
In this section, I will pinpoint some of the numerous practical applications of the dot product.
Mechanics and physics
The dot product calculates work (W = F.d) and power. I mentioned this earlier. What I didn't have to time to mention is that it is also invariant under rotations and coordinate transformations, which makes it a suitable tool for physical laws expressed in different frames.
Computer graphics and game development
Geometry is a central component of computer graphics, and the dot product is the central component of analytical geometry. For example, it supports field-of-view checks and lighting via normal-dot-light vectors. It is also used for collision detection through plane equations and shading computations.
Signal processing and machine learning
The dot product measures similarity in high-dimensional spaces. It is used for convolution, neural network layers (as weighted sums), and recommendation systems. In word embeddings, cosine similarity (normalized dot product) compares semantic vectors, and this holds a great significance in Retrieval Augmented Generation, for example.
How to Calculate Dot Product in Python, R, and Excel
The dot product can be computed efficiently in different programming environments. In this section, I will show some examples of different ones.
Dot product in Python
Python has a lot of implementation choices for the dot product. NumPy offers np.dot(a,b) or the @ operator for efficient vector/matrix operations.
A pure Python version uses sum(ai * bi for ai, bi in zip(a,b)).
For arrays/matrices, broadcasting and vectorization cause an important performance gain. Here's what I mean:
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(np.dot(a, b)) # 32
print(a @ b) # 32Dot product in R
R’s %*% handles matrix multiplication, while crossprod(a, b) or sum(a * b) provide alternatives.
As mentioned, vectorization speeds up the calculations in base R and also in packages like Matrix.
a <- c(1, 2, 3)
b <- c(4, 5, 6)
a %*% b # returns matrix with 32
sum(a * b) # 32Dot product in Excel
Use =SUMPRODUCT(A2:A4, B2:B4) for vectors in columns A and B. Or, multiply pairwise and sum manually.
For larger datasets, array formulas or Power Query are better, though Excel would still have scalability limitations compared to programmatic tools.
For fun, read our tutorials on Cartesian Product in SQL: A Comprehensive Guide and What Is a Data Product? Concepts and Best Practices.
Performance comparison across platforms
NumPy in Python outperforms pure Python loops and scales very well for large data via optimized BLAS libraries because of its precise implementation and allocation styles.
R’s vectorization, on the other hand, is efficient for moderate sizes.
Excel suits small datasets or quick prototyping, but underperforms for large-scale analysis. Specialized libraries generally provide superior performance metrics.
Advanced Dot Product Concepts
Dot products are more than just calculating similarities in Rn, in this section, I’ll explain why.
Function spaces and integrals
In function spaces such as L2, the inner product generalizes to:
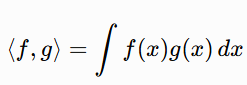
With applications in Fourier analysis.
Weighted inner products and matrix dot products
Weighted versions use a positive definite matrix; the Frobenius inner product for matrices is:
![]()
Tensor generalizations extend the concept to higher orders.
Relativistic physics
The Minkowski metric yields:
![]()
This departs from the Euclidean case for spacetime intervals.
Vector similarity metrics
Since the dot product of two vectors A and B is
![]()
Then, by dividing the norms of A and B from both sides, we get the cosine similarity:
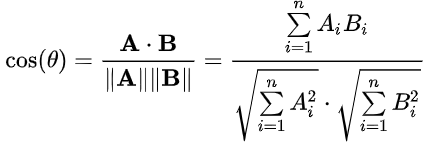
Cosine similarity normalizes the dot product and is widely used in information retrieval and machine learning.
Eigenvalue decomposition
Explore the connection between dot products and symmetric matrices. Discuss orthogonality and matrix factorizations. Note relevance to principal component analysis and spectral theory.
Dot Product vs. Cross Product
This section contrasts the dot product with the cross product.
Scalar and vector projections
A Scalar projection gives magnitude along a certain direction. A vector projection, on the other hand, shows the parallel component. These support component decomposition with geometric illustrations.
Triple product and cross product comparison
The scalar triple product is:
![]()
which gives a signed volume. The dot product here gives a scalar while the cross product produces a vector. Use the dot product for similarity or alignments and the cross product for orientation or rotation.
|
Aspect |
Dot Product |
Cross Product |
|
Result |
Scalar |
Vector |
|
Use |
Angle, work, similarity |
Torque, area, perpendicular |
|
Dimension |
Any |
3D (primarily) |
|
Zero When |
Orthogonal |
Parallel |
This table shows some main differences between the two products.
Invariance under rotations and coordinate transformations
The dot product stays unchanged under orthogonal transformations, which is a very good property in physics and engineering for coordinate-independent formulations. There are, of course, many different types of multiplication with different significance and calculation methods. Check out our tutorial on Hadamard Product: A Complete Guide to Element-Wise Matrix Multiplication to see an example.
Conclusion
In summary, the dot product is a versatile and foundational tool in mathematics that is used in different fields such as physics and computer science. Its applications range from work calculations and lighting models to high-dimensional data similarity, which pinpoint its continued relevance. Therefore, I believe these perspectives encourage further exploration of the advanced generalizations. Enroll in our Linear Algebra for Data Science in R course to keep learning.
I work on accelerated AI systems enabling edge intelligence with federated ML pipelines on decentralized data and distributed workloads. Mywork focuses on Large Models, Speech Processing, Computer Vision, Reinforcement Learning, and advanced ML Topologies.
Dot Product FAQs
What is a dot product in simple terms?
In simple terms, the dot product multiplies matching parts of two lists (vectors) and adds them up. You can think of the resulting scalar as how much the vectors point together. For example, aligned vectors give a large positive value.
How do you find the dot product of two vectors?
Multiply corresponding components to get a new vector and then sum all of its components. Alternatively, use magnitudes and the cosine of the angle to calculate it. Both approaches are equivalent.
What does a negative dot product mean?
A negative value indicates an obtuse angle. This means that the vectors point in somewhat opposing directions.
What is the difference between dot product and cross product?
The dot product is a scalar measuring the alignment, while the cross product is a vector perpendicular to both with a magnitude equal to the parallelogram area.
Why is dot product called scalar product?
It produces a scalar (single number) rather than an entity (vector, matrix, function…). Hence, the historical term “scalar product.”
How does the dot product relate to the angle between two vectors?
a · b = |a| |b| cos θ. Positive for acute angles, zero at 90°, negative for obtuse angles.
Can you explain the geometric interpretation of the dot product?
It measures how much one vector projects onto another — maximum when parallel, zero when perpendicular, negative when opposing
What are some practical applications of the dot product in physics?
Calculates work (F · d), power (F · v), and resolves forces into components.
How is the dot product used in machine learning and deep learning?
Computes similarity via cosine, powers neural network layers, attention mechanisms, and word embeddings comparison.
What are the differences between the dot product and the cross product?
Dot product yields a scalar (alignment, any dimension); cross product yields a perpendicular vector (area/torque, mainly 3D)

