8 modèles d'apprentissage automatique expliqués en 20 minutes

Pourquoi utiliser des modèles d'apprentissage automatique ?

Aujourd'hui, de nombreuses grandes entreprises utilisent une forme ou une autre de modélisation prédictive pour maximiser leur chiffre d'affaires et stimuler leur croissance.

L'apprentissage automatique est utilisé dans de nombreux domaines. Les plateformes d'abonnement comme Netflix et Spotify, par exemple, utilisent l'apprentissage automatique pour recommander des contenus en fonction de l'activité de l'utilisateur sur l'application. 

Les systèmes de recommandation apportent une valeur ajoutée directe à ces entreprises, car une meilleure expérience utilisateur incitera les clients à continuer à s'abonner à la plateforme. Il s'agit d'un exemple de modèle d'apprentissage automatique non supervisé.

De même, un fournisseur de services mobiles peut utiliser l'apprentissage automatique pour analyser le sentiment des utilisateurs et adapter son offre de produits à la demande du marché. Il s'agit d'un exemple de modèle d'apprentissage automatique supervisé.

Tous les modèles d'apprentissage automatique peuvent être classés comme supervisés ou non supervisés. La principale différence entre les deux est qu'un algorithme supervisé nécessite des données d'entrée et de sortie étiquetées, tandis qu'un modèle non supervisé peut traiter des ensembles de données brutes, non étiquetées.

Les modèles d'apprentissage automatique supervisé peuvent ensuite être classés en algorithmes de régression et de classification, qui seront expliqués plus en détail dans cet article.

Apprentissage automatique des modèles de régression

Les algorithmes de régression sont utilisés pour prédire un résultat continu (y) à l'aide de variables indépendantes (x). 

Par exemple, regardez le tableau ci-dessous :

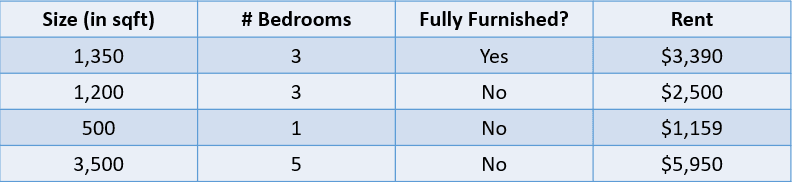
Image de l'auteur

Dans ce cas, nous aimerions prédire le loyer d'une maison en fonction de sa taille, du nombre de chambres et du fait qu'elle soit ou non entièrement meublée. La variable dépendante, "Loyer", est numérique, ce qui en fait un problème de régression. 

Un problème comportant de nombreuses variables d'entrée, comme celui présenté ci-dessus, est appelé problème de régression à plusieurs variables.

Métriques de régression

Les débutants en science des données pensent souvent à tort qu'un modèle de régression peut être évalué à l'aide d'une mesure telle que la précision. La précision est une mesure utilisée pour évaluer les performances des modèles de classification, comme nous l'expliquerons plus loin dans cet article.

Les modèles de régression, quant à eux, sont évalués à l'aide de mesures telles que l'erreur absolue moyenne (MAE), l'erreur quadratique moyenne (MSE) et l'erreur quadratique moyenne (RMSE).

Ajoutons une valeur prédite au problème du prix de l'immobilier ci-dessus et évaluons ces prédictions à l'aide de quelques mesures de régression :

Image de l'auteur

1. Erreur absolue moyenne : 

L'erreur absolue moyenne calcule la somme de la différence entre toutes les valeurs réelles et prédites, et la divise par le nombre total d'observations. Voici la formule pour calculer la MAE :

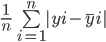
Calculons l'erreur absolue moyenne des valeurs ci-dessus à l'aide de cette formule :

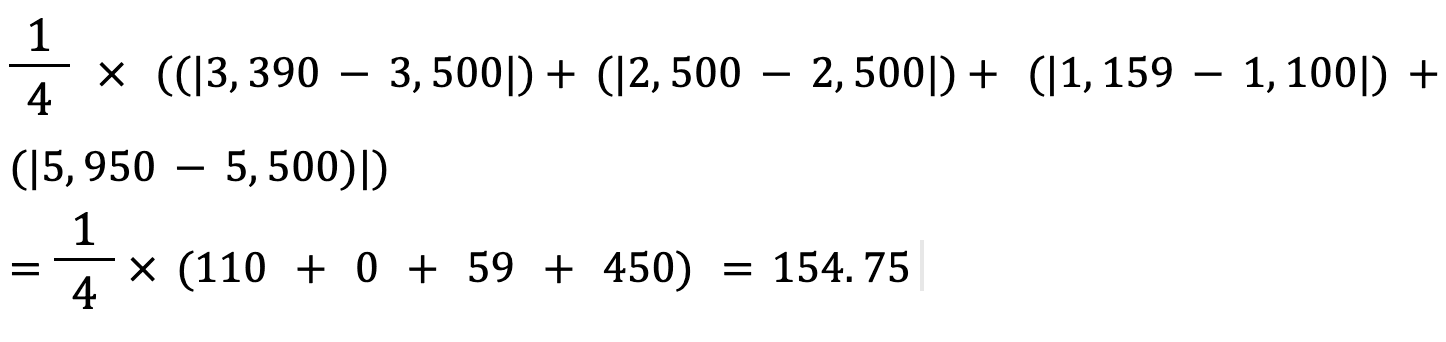
L'erreur absolue moyenne entre le prix réel et le prix prédit est d'environ 155 $.

2. Erreur quadratique moyenne : 

La formule de calcul de l'erreur quadratique moyenne d'un modèle est similaire à celle de l'erreur absolue moyenne :

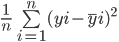
Notez que l'erreur absolue moyenne calcule la distance absolue moyenne entre la valeur réelle et la valeur prédite, tandis que l'erreur quadratique moyenne calcule la distance quadratique moyenne entre la valeur réelle et la valeur prédite.

Calculons l'EQM entre les valeurs réelles et prédites ci-dessus :

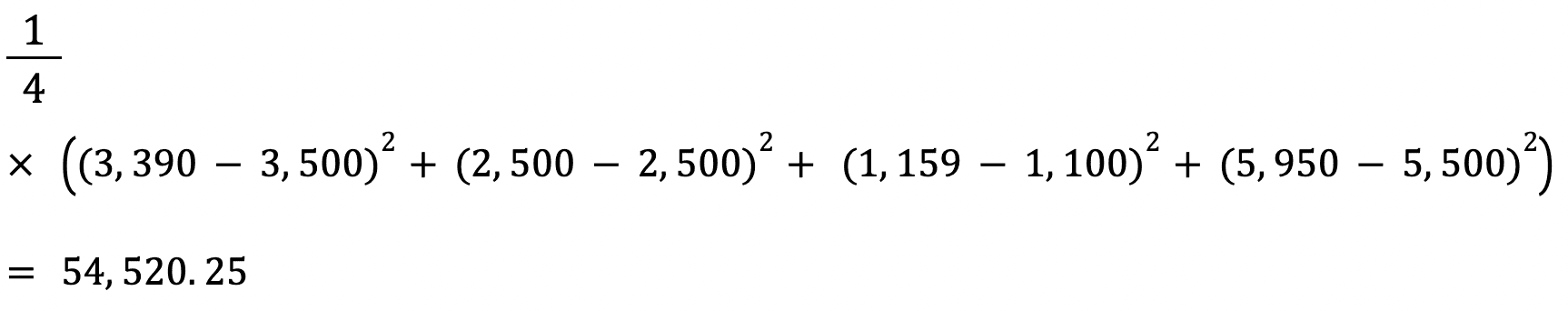
3. Erreur quadratique moyenne : 

La RMSE d'un estimateur est calculée en trouvant la racine carrée de son erreur quadratique moyenne. L'un des avantages du calcul de la RMSE d'un ensemble de données par rapport à la MSE est que l'erreur est exprimée dans la même unité que la variable que nous prédisons.

Dans ce cas, par exemple, le RMSE est de √54,520.25=233.5. Cette valeur est interprétable puisqu'elle est exprimée en termes de prix du logement, alors que l'erreur quadratique moyenne ne l'est pas.

Maintenant que vous comprenez le concept de régression, examinons les différents types de modèles de régression :

Régression linéaire simple

La régression linéaire est une approche linéaire de la modélisation de la relation entre une variable dépendante et une ou plusieurs variables indépendantes. Cet algorithme consiste à trouver la ligne qui correspond le mieux aux données disponibles. 

Voici une représentation visuelle du fonctionnement d'un modèle de régression linéaire simple :

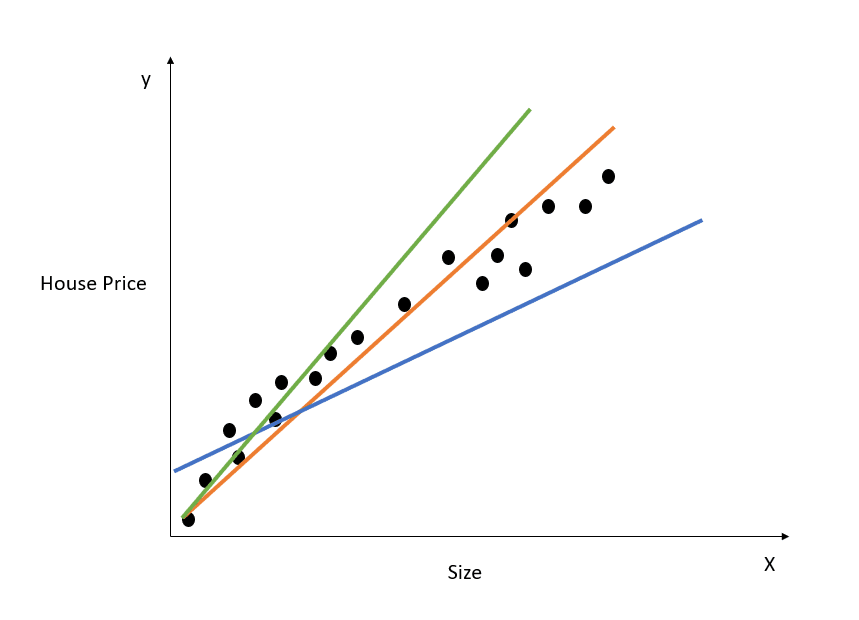
Image de l'auteur

Le graphique ci-dessus illustre la relation entre le prix des logements et leur taille. Le modèle de régression linéaire crée une ligne qui modélise au mieux cette relation. Toutes les prévisions de prix de l'immobilier relatives à différentes valeurs de la taille se situent sur la ligne de meilleur ajustement.

Observez que trois lignes sont tracées sur le schéma ci-dessus. Laquelle de ces lignes est la "ligne de meilleur ajustement" ?

Ligne de meilleur ajustement

Il suffit de regarder le diagramme ci-dessus pour constater que la ligne orange est la plus proche de tous les points de données présentés. On peut donc dire intuitivement qu'elle représente la "ligne de meilleur ajustement". 

Voici une explication plus formelle de la manière dont la ligne de meilleure adaptation est trouvée dans la régression linéaire :

L'équation d'une ligne droite est y=mx+c. Ici, m représente la pente de la droite et c son ordonnée à l 'origine . Il existe une infinité de façons de tracer cette ligne, car il existe une infinité de valeurs possibles pour m et c.

La ligne de meilleur ajustement, également connue sous le nom de ligne de régression des moindres carrés, est trouvée en minimisant la somme des carrés de la distance entre la valeur réelle et la valeur prédite :

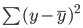
Vous pouvez lire le tutoriel Essentials of Linear Regression in Python pour mieux comprendre le modèle d'apprentissage automatique de régression linéaire et sa mise en œuvre.

Régression des crêtes

La régression ridge est une extension du modèle de régression linéaire expliqué ci-dessus. Il s'agit d'une technique utilisée pour maintenir les coefficients d'un modèle de régression aussi bas que possible.

L'un des problèmes d'un modèle de régression linéaire simple est que ses coefficients peuvent devenir importants, ce qui rend le modèle plus sensible aux données d'entrée. Cela peut conduire à un surajustement.

Prenons un exemple simple pour comprendre le concept d'overfitting :

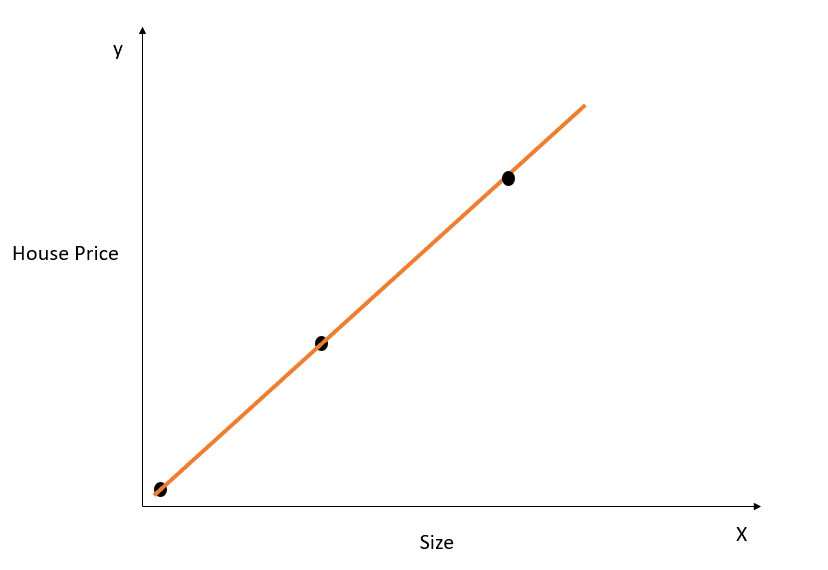
Image de l'auteur

Dans la figure ci-dessus, la droite de meilleur ajustement modélise parfaitement la relation entre X et y, et la somme des carrés entre la valeur réelle et la valeur prédite est de 0. Rappelez-vous que l'équation de cette droite est y=mx+c.

Bien que cette ligne soit parfaitement adaptée à l'ensemble de données d'apprentissage, elle ne se généraliserait probablement pas bien aux données de test. Ce phénomène s'appelle l'overfitting, et vous pouvez lire cet article sur l'overfitting pour en savoir plus.

En d'autres termes, un modèle très complexe va saisir des nuances inutiles de l'ensemble de données d'apprentissage qui ne se reflètent pas dans le monde réel. Ce modèle sera extrêmement performant sur les données d'entraînement, mais moins performant sur les ensembles de données autres que ceux sur lesquels il a été entraîné.

Un modèle de régression linéaire avec de grands coefficients est susceptible d'être surajouté.

La régression ridge est une technique de régularisation qui oblige l'algorithme à choisir des coefficients plus petits en pénalisant sa fonction de perte pour inclure un coût supplémentaire.

Comme indiqué dans la section précédente, voici l'erreur que nous voulons minimiser dans une régression linéaire simple :

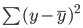
Dans la régression ridge, cette équation est légèrement modifiée et un terme de pénalité est ajouté à l'erreur ci-dessus :

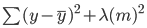
Notez qu'il y a une valeur (lambda) multipliée aux coefficients du modèle. Comme ce modèle ne comporte qu'une seule variable, il n'y a qu'un seul coefficient auquel est ajouté un terme de pénalité. S'il y a plusieurs variables indépendantes, lambda sera multiplié par la somme des coefficients au carré. 

Ce terme de pénalité punit le modèle pour avoir choisi des coefficients plus importants. L'objectif est de réduire les valeurs des coefficients de manière à ce que les variables ayant une contribution mineure au résultat aient des coefficients proches de 0. Cela permet de réduire la variance du modèle et d'atténuer l'adaptation excessive.

Quelle est la valeur lambda optimale pour la régression ridge ?

Observez qu'une valeur lambda de 0 n'aura aucun effet et que le terme de pénalité est éliminé. Une valeur plus élevée de lambda ajoutera une pénalité de rétrécissement plus importante, et les coefficients du modèle se rapprocheront de zéro. 

Lorsque vous choisissez une valeur lambda, veillez à trouver un équilibre entre la simplicité et une bonne adaptation aux données d'apprentissage. Une valeur lambda plus élevée permet d'obtenir un modèle simple et généralisé, mais le choix d'une valeur trop élevée comporte le risque d'un sous-ajustement. En revanche, le choix d'une valeur de lambda très proche de zéro peut conduire à un modèle très complexe. 

Régression Lasso

La régression Lasso est une autre extension de la régression linéaire qui réduit les coefficients du modèle en ajoutant un terme de pénalité à sa fonction de coût.

Voici l'erreur qui doit être minimisée dans la régression lasso :

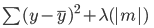
Remarquez que cette équation est semblable à celle d'un modèle de régression ridge, sauf qu'au lieu de multiplier lambda par le carré du coefficient, nous le multiplions par la valeur absolue du coefficient.

La principale différence entre la régression ridge et la régression lasso réside dans le fait que, dans la régression ridge, les coefficients du modèle peuvent se rapprocher de zéro, mais ne deviennent jamais nuls. Dans la régression lasso, il est possible que les coefficients du modèle deviennent nuls. 

Si le coefficient d'une variable indépendante atteint zéro, la caractéristique peut être éliminée du modèle. Cela réduit l'espace des caractéristiques et rend l'algorithme plus facile à interpréter, ce qui est le principal avantage de la régression lasso. 

De ce fait, la régression lasso peut également être utilisée comme technique de sélection des caractéristiques, puisque les variables de faible importance peuvent avoir des coefficients qui atteignent zéro et seront entièrement supprimées du modèle. 

Comment construire un modèle d'apprentissage automatique de régression en Python ?

Vous pouvez construire des modèles de régression linéaire, ridge et lasso à l'aide de la bibliothèque Scikit-Learn :

1. Régression linéaire

from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()

Pour ajuster le modèle sur votre ensemble de données d'entraînement, exécutez :

lr_model.fit(X_train,y_train)

2. Régression des crêtes

from sklearn.linear_model import Ridge
model = Ridge(alpha=1.0)

Le terme lambda peut être configuré via le paramètre "alpha" lors de la définition du modèle. 

3. Régression Lasso

from sklearn.linear_model import Lasso
model = Lasso(alpha=1.0)

Si vous souhaitez en savoir plus sur les modèles linéaires et sur la manière de les construire en Python, suivez notre cours Introduction à la modélisation linéaire en Python.

Modèles de classification par apprentissage automatique

Nous utilisons des algorithmes de classification pour prédire un résultat discret (y) à l'aide de variables indépendantes (x). La variable dépendante, dans ce cas, est toujours une classe ou une catégorie. 

Par exemple, prédire si un patient est susceptible de développer une maladie cardiaque en fonction de ses facteurs de risque est un problème de classification :

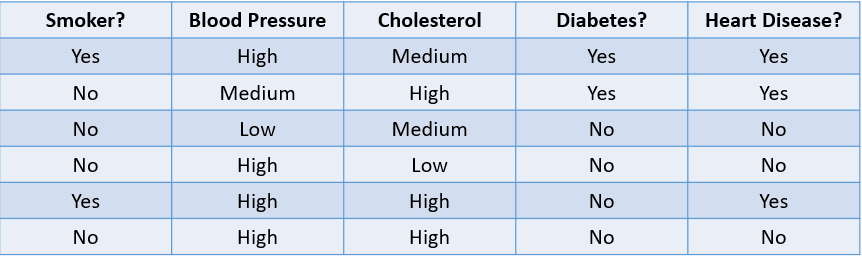
Image de l'auteur

Le tableau ci-dessus illustre un problème de classification avec quatre variables indépendantes et une variable dépendante, les maladies cardiaques. Comme il n'y a que deux résultats possibles (oui et non), on parle de problème de classification binaire. 

Parmi les autres exemples de problèmes de classification binaire, on peut citer la classification d'un courriel en spam ou légitime, la prédiction du taux d'attrition des clients et la décision d'accorder ou non un prêt à quelqu'un.

Un problème de classification multiclasse est un problème qui comporte trois résultats possibles ou plus, comme les prévisions météorologiques ou la distinction entre différentes espèces animales.

Métriques de classification

Il existe de nombreuses façons d'évaluer un modèle de classification. Si la précision est la mesure la plus utilisée, elle n'est pas toujours la plus fiable.

Examinons quelques méthodes courantes utilisées pour évaluer un algorithme de classification sur la base de l'ensemble de données ci-dessous :

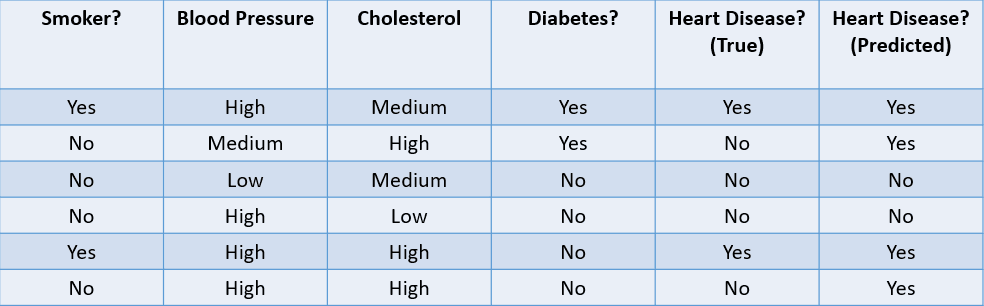
Image de l'auteur

1. Précision: La précision peut être définie comme la fraction de prédictions correctes faites par le modèle d'apprentissage automatique.

La formule pour calculer la précision est la suivante :

Dans ce cas, la précision est de 46, soit 0,67.

2. Précision: La précision est une mesure utilisée pour calculer la qualité des prédictions positives faites par le modèle. Il est défini comme suit :

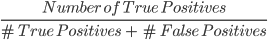
Le modèle ci-dessus a une précision de 24, soit 0,5.

3. Rappel: Le rappel est utilisé pour calculer la qualité des prédictions négatives faites par le modèle. Il est défini comme suit :

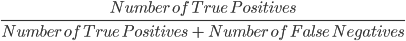
Le modèle ci-dessus a un rappel de 2/2 ou 1.

Prenons un exemple simple pour comprendre la différence entre précision et rappel :

Il existe une maladie rare et mortelle qui touche une fraction de la population. 95 % des patients figurant dans la base de données d'un hôpital ne sont pas atteints de la maladie, tandis que 5 % seulement le sont. Si nous construisons un algorithme d'apprentissage automatique qui prédit que personne n'est atteint de la maladie, la précision d'apprentissage de ce modèle sera de 95 %. Malgré cette précision élevée, nous savons qu'il ne s'agit pas d'un bon modèle puisqu'il ne permet pas d'identifier les patients atteints de la maladie.

C'est là qu'interviennent des mesures telles que la précision et le rappel. La précision, ou spécificité, indique la capacité du modèle à identifier correctement les personnes ne souffrant pas de la maladie. Le rappel, ou sensibilité, nous indique dans quelle mesure le modèle identifie les personnes atteintes de la maladie.

Une "bonne" valeur de précision et de rappel est subjective et dépend de votre cas d'utilisation. 

Dans ce scénario de prédiction de la maladie, nous voulons toujours identifier les personnes atteintes de la maladie, même si cela comporte le risque d'un faux positif. Ici, nous construirons le modèle de manière à ce que le rappel soit plus élevé que la précision.

D'autre part, si nous devions construire un modèle qui empêche les acteurs malveillants d'entrer sur un site de commerce électronique, nous pourrions souhaiter une plus grande précision, car le blocage des utilisateurs légitimes entraînera une baisse des ventes.

Nous utilisons souvent une mesure appelée F1-Score pour trouver la moyenne harmonique de la précision et du rappel d'un classificateur. En termes simples, le score F1 combine la précision et le rappel en une seule mesure en calculant leur moyenne. 

L'aire sous la courbe (AUC) est une autre mesure populaire utilisée pour évaluer les performances d'un modèle de classification. L'AUC d'un algorithme nous renseigne sur sa capacité à faire la distinction entre les classes positives et négatives.

Pour en savoir plus sur les mesures telles que l'AUC et leur mode de calcul, suivez le cours Supervised Learning in R de DataCamp.

Examinons maintenant les différents types de modèles de classification et leur fonctionnement :

Régression logistique

La régression logistique est un modèle de classification simple qui prédit la probabilité qu'un événement se produise.

Voici un exemple du fonctionnement du modèle de régression logistique :

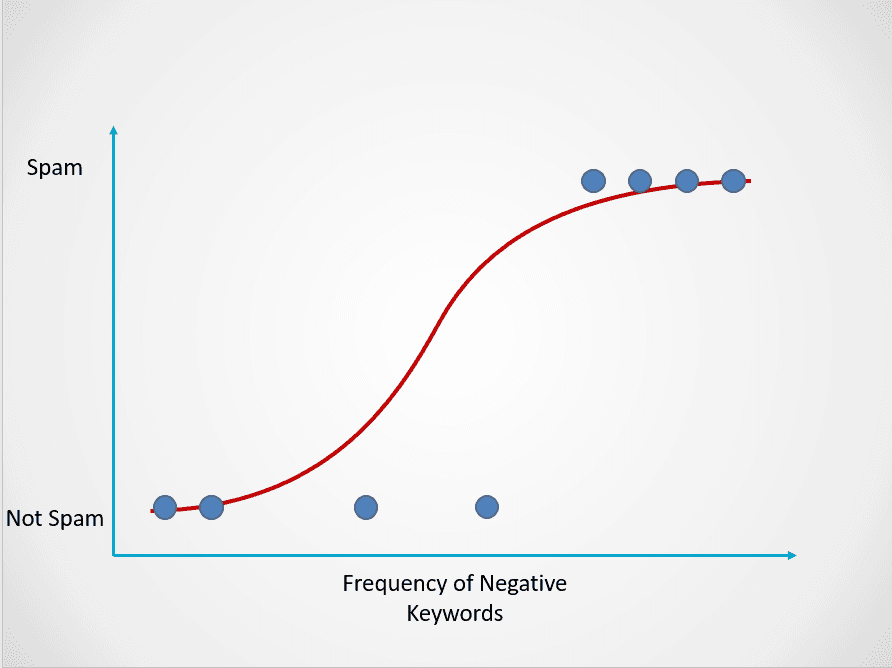
Image de l'auteur

Le graphique ci-dessus présente une fonction logistique qui répartit les données des courriers électroniques en deux catégories : "Spam" et "Pas de spam" en fonction de la fréquence des mots-clés négatifs dans le texte.

Observez que, contrairement à l'algorithme de régression linéaire, la régression logistique est modélisée par une courbe en forme de S. Cette fonction est connue sous le nom de fonction logistique et a la formule suivante :

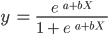
Alors que la fonction linéaire n'a pas de limite supérieure ou inférieure, la fonction logistique est comprise entre 0 et 1. Le modèle prédit une probabilité comprise entre 0 et 1, qui détermine la classe à laquelle appartient le point de données.

Dans cet exemple de courrier indésirable, si le texte contient peu ou pas de mots-clés suspects, la probabilité qu'il s'agisse d'un courrier indésirable est faible et proche de 0. En revanche, un courriel contenant de nombreux mots-clés suspects aura une probabilité élevée d'être un spam, proche de 1.

Cette probabilité est ensuite transformée en un résultat de classification :

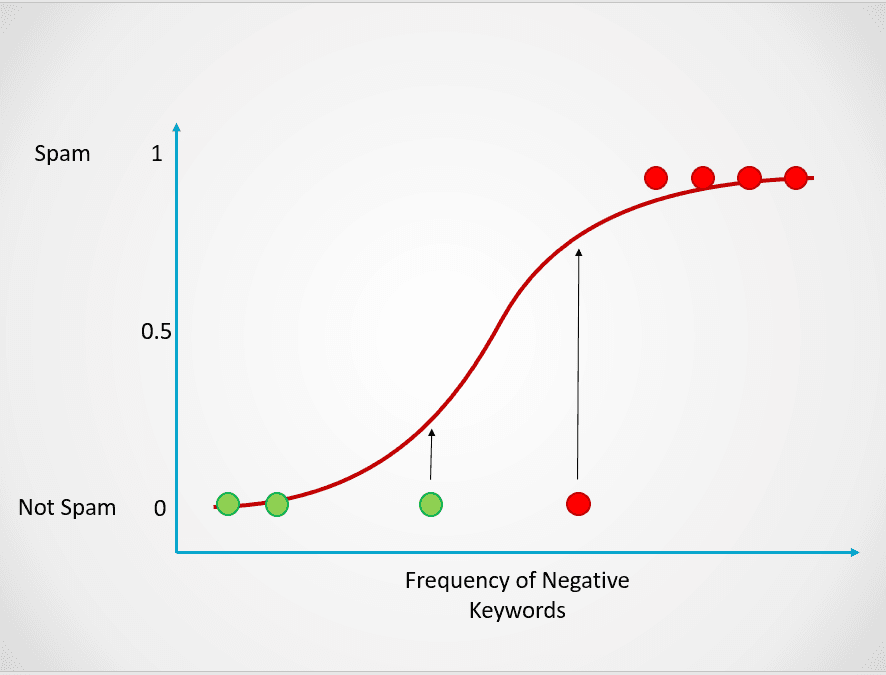
Image de l'auteur

Tous les points colorés en rouge ont une probabilité >= 0,5 d'être des spams. Ils sont donc classés comme spam et le modèle de régression logistique donnera un résultat de classification de 1. Les points colorés en vert ont une probabilité < 0,5 d'être du spam, ils sont donc classés par le modèle comme "Pas de spam" et renverront un résultat de classification de 0.

Pour les problèmes de classification binaire tels que ceux décrits ci-dessus, le seuil par défaut d'un modèle de régression logistique est de 0,5, ce qui signifie que les points de données dont la probabilité est supérieure à 0,5 se verront automatiquement attribuer une étiquette de 1. Cette valeur seuil peut être modifiée manuellement en fonction de votre cas d'utilisation pour obtenir de meilleurs résultats.

Rappelez-vous qu'en régression linéaire, nous avons trouvé la ligne d'ajustement optimale en minimisant la somme des carrés de l'erreur entre les valeurs prédites et les valeurs réelles. Dans la régression logistique, cependant, les coefficients sont estimés à l'aide d'une technique appelée estimation du maximum de vraisemblance au lieu des moindres carrés.

Lisez le tutoriel sur la régression logistique de Python pour en savoir plus sur le concept d'estimation du maximum de vraisemblance et sur le fonctionnement de la régression logistique.

Voisins les plus proches (K-Nearest Neighbors)

Le KNN est un algorithme de classification qui classe un point de données en fonction du groupe auquel appartiennent les points de données les plus proches.

Voici un exemple simple qui illustre le fonctionnement du modèle des K-voisins les plus proches :

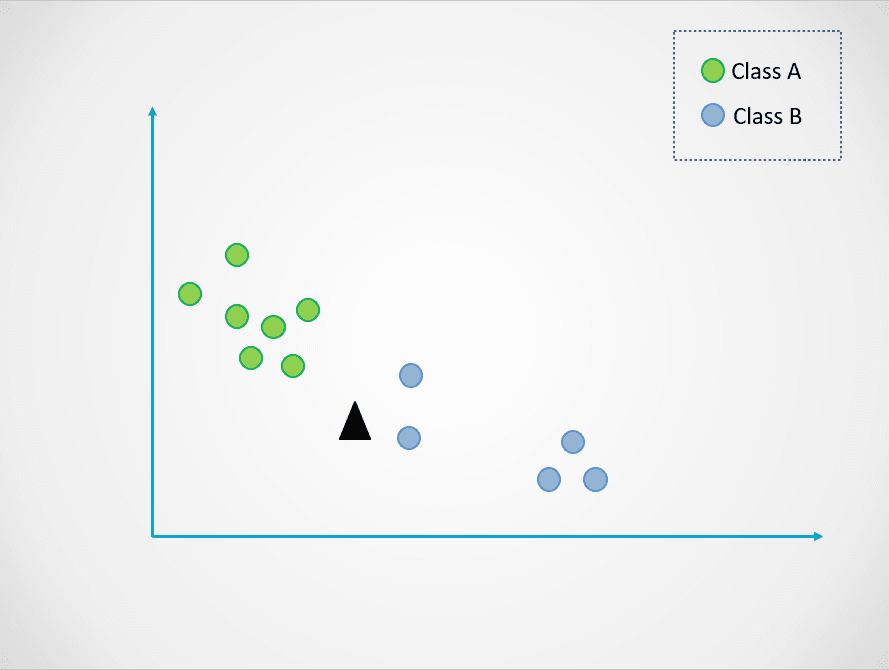
Image de l'auteur

Dans le diagramme ci-dessus, il y a deux classes de points de données - A et B. Le triangle noir représente un nouveau point de données qui doit être classé dans l'une de ces deux classes.

L'algorithme des K-voisins les plus proches fonctionne comme suit :

• Étape 1: Le modèle stocke d'abord toutes les données d'apprentissage.
• Étape 2 : Il calcule ensuite la distance entre le nouveau point de données et tous les points de l'ensemble de données.
• Étape 3: Le modèle trie ces points de données en fonction de leur distance par rapport au nouveau point de données.
• Étape 4: Le nouveau point de données est affecté à la classe de ses voisins les plus proches en fonction de la valeur de "k".

Dans le graphique ci-dessus, la valeur de k est 1. Cela signifie que nous ne prenons en compte que le plus proche voisin du triangle noir et que nous attribuons le point de données à cette classe. Le nouveau point de données étant le plus proche du point bleu, nous l'affectons à la classe B.

Modifions maintenant la valeur de k. Essayons deux valeurs possibles de k, 3 et 7 :

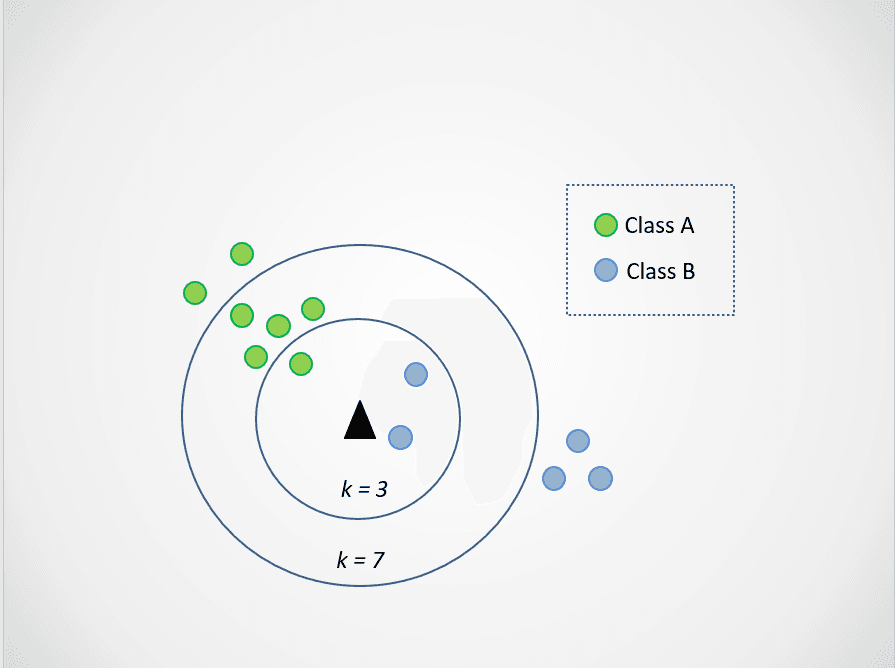
Image de l'auteur

Remarquez maintenant que lorsque nous choisissons k=3, le nouveau point de données se situe entre deux catégories. Cela signifie que nous choisissons la classe majoritaire. Deux voisins les plus proches sont bleus et un voisin le plus proche est vert. Le point de données sera donc à nouveau attribué à la classe des points bleus, la classe B.

Lorsque k=7, cependant, les choses changent. Maintenant, deux voisins les plus proches sont bleus et sept sont verts. Dans ce cas, le point de données sera attribué à la classe verte, la classe A.

Le choix de différentes valeurs de k aura un impact sur la classe à laquelle le nouveau point sera affecté. 

La sélection d'une valeur trop faible peut être bruyante et sujette à des valeurs aberrantes, tandis que la sélection d'une valeur élevée peut vous faire négliger des catégories comportant moins de points de données.

Si vous souhaitez en savoir plus sur l'algorithme des K-voisins les plus proches et sur la manière de sélectionner une valeur "k" optimale, lisez ce tutoriel KNN.

Construire un modèle de classification en Python

Voici quelques extraits de code que vous pouvez utiliser pour construire un modèle de classification en Python à l'aide de la bibliothèque Scikit-Learn :

1. Régression logistique

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()

2. Voisins les plus proches (K-Nearest Neighbors)

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()

Apprentissage automatique Modèles arborescents

Les modèles arborescents sont des algorithmes d'apprentissage automatique supervisé qui construisent une structure arborescente pour faire des prédictions. Ils peuvent être utilisés pour les problèmes de classification et de régression.

Dans cette section, nous examinerons deux des modèles d'apprentissage automatique basés sur les arbres les plus couramment utilisés : les arbres de décision et les forêts aléatoires.

Arbres de décision

Un arbre de décision est l'algorithme d'apprentissage automatique le plus simple basé sur un arbre. Ce modèle nous permet de diviser continuellement l'ensemble des données en fonction de paramètres spécifiques jusqu'à ce qu'une décision finale soit prise.

Voici un exemple simple illustrant le fonctionnement de l'algorithme de l'arbre de décision :

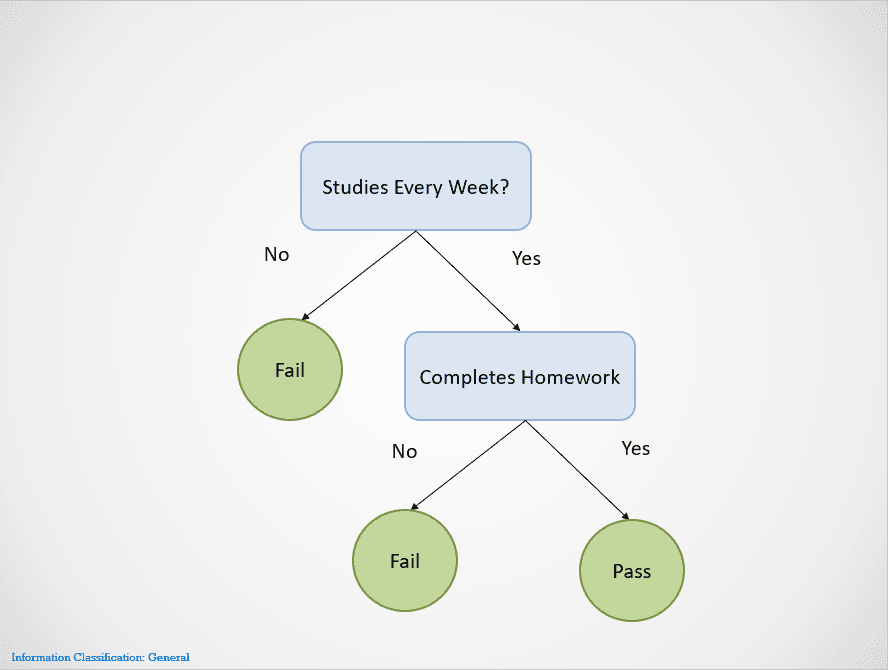
Image de l'auteur

Les arbres de décision se divisent en différents nœuds jusqu'à ce qu'un résultat soit obtenu. 

Dans ce cas, si un étudiant n'étudie pas chaque semaine, il échouera. S'il étudie chaque semaine mais ne fait pas ses devoirs, le résultat est toujours "Échec". Ils ne réussiront que s'ils étudient chaque semaine et s'ils terminent tous leurs devoirs.

Remarquez que l'arbre de décision ci-dessus se divise d'abord sur la variable "Études chaque semaine". Si la réponse est "Non", il arrête le fractionnement et indique que l'élève échoue. 

L'arbre de décision choisira une variable à diviser en premier sur la base d'une métrique appelée entropie. Il cessera de diviser lorsque vous obtiendrez une "division pure", c'est-à-dire lorsque tous les points de données appartiendront à une seule classe.

Il existe de nombreuses façons de construire un arbre de décision. L'arbre doit trouver un élément à diviser en premier, deuxième, troisième, etc. Cette structure est créée sur la base d'une mesure appelée gain d'information. Le meilleur arbre de décision possible est celui qui offre le gain d'information le plus élevé.

Pour en savoir plus sur le fonctionnement des arbres de décision, ainsi que sur les mesures telles que l'entropie et le gain d'information, cet article sur la classification par arbre de décision de Python contient plus de détails.

L'un des principaux avantages des arbres de décision est qu'ils sont très faciles à interpréter. Il est facile de travailler à rebours et de comprendre comment un arbre de décision a obtenu son résultat final sur la base de l'ensemble de données d'apprentissage.

Cependant, les arbres de décision sont également très enclins à l'overfitting si on les laisse se développer complètement. En effet, ils sont conçus pour se diviser parfaitement sur tous les échantillons de l'ensemble de données d'apprentissage, ce qui les rend incapables de bien se généraliser aux données externes.

Cet inconvénient des arbres de décision peut être résolu en utilisant l'algorithme de la forêt aléatoire.

Forêts aléatoires

Le modèle de forêt aléatoire est un algorithme basé sur un arbre qui nous aide à atténuer certains des problèmes qui surviennent lors de l'utilisation d'arbres de décision, l'un d'entre eux étant l'adaptation excessive. Les forêts aléatoires sont créées en combinant les prédictions faites par plusieurs modèles d'arbres de décision et en renvoyant un seul résultat.

Il le fait en deux étapes :

• Étape 1: Tout d'abord, les lignes et les variables de l'ensemble de données sont échantillonnées au hasard avec remplacement. Plusieurs arbres de décision sont ensuite créés et entraînés sur chaque échantillon de données. 
• Étape 2: Ensuite, les prédictions faites par tous ces arbres de décision sont combinées pour obtenir une sortie unique. Par exemple, si trois arbres de décision distincts ont été formés et que deux d'entre eux ont prédit "Oui" et un "Non", le résultat final de l'algorithme de la forêt aléatoire sera "Oui".

Dans le cas d'un problème de régression, le résultat sera la prédiction moyenne de tous les arbres de décision.

Voici un simple visuel pour illustrer le fonctionnement de l'algorithme de la forêt aléatoire :

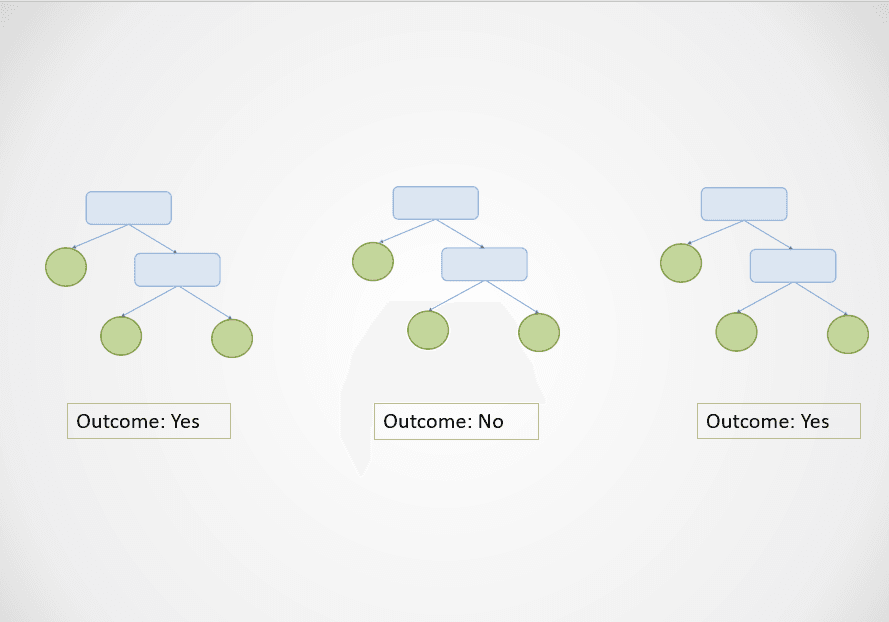
Image de l'auteur

Dans le diagramme ci-dessus, les premier et troisième arbres de décision prédisent "Oui", tandis que le deuxième prédit "Non".

Comme il s'agit d'une tâche de classification, la classe majoritaire est sélectionnée. Dans ce cas, l'algorithme de la forêt aléatoire donnera le résultat final "Oui" sur la base des prédictions faites par 2 des 3 arbres de décision.

L'un des principaux avantages de l'algorithme de la forêt aléatoire est qu'il se généralise bien, puisqu'il combine les résultats de plusieurs arbres de décision formés sur un sous-ensemble de caractéristiques.

En outre, alors que le résultat d'un seul arbre de décision peut varier considérablement en fonction d'une petite modification de l'ensemble de données d'apprentissage, ce problème ne se pose pas avec l'algorithme de forêt aléatoire, car l'ensemble de données d'apprentissage est échantillonné de nombreuses fois.

Construire un modèle arborescent en Python

Exécutez les lignes de code suivantes pour créer un algorithme d'apprentissage automatique basé sur des arbres avec Scikit-Learn :

1. Arbre de décision 

# classification

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()

# regression

from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor()

2. Forêts aléatoires

# classification

from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier()

# regression

from sklearn.ensemble import RandomForestRegressor
rf_reg = RandomForestRegressor()

Machine Learning Clustering

Jusqu'à présent, nous avons exploré les modèles d'apprentissage automatique supervisé pour résoudre les problèmes de classification et de régression. Nous allons maintenant nous pencher sur une approche d'apprentissage non supervisé très répandue, appelée "clustering".

En d'autres termes, le regroupement consiste à créer un groupe d'objets qui sont similaires les uns aux autres mais différents des autres. Cette technique est utilisée dans de nombreux cas par les entreprises, notamment pour recommander des films aux utilisateurs ayant des habitudes de visionnage similaires sur un site de streaming vidéo, pour la détection d'anomalies et pour la segmentation de la clientèle.

Dans cette section, nous examinerons un algorithme appelé K-Means clustering - le modèle d'apprentissage automatique le plus simple et le plus populaire utilisé pour les tâches d'apprentissage non supervisé.

Regroupement K-Means

Le regroupement K-Means est une technique d'apprentissage automatique non supervisée qui est utilisée pour regrouper des objets similaires dans des données.

Voici un exemple du fonctionnement de l'algorithme de regroupement K-Means :

Image de l'auteur

Étape 1: L'image ci-dessus est constituée d'observations non étiquetées qui n'ont pas été regroupées. Dans un premier temps, chaque observation est affectée à une grappe de manière aléatoire. Un centroïde est ensuite calculé pour chaque groupe. 

Ils sont représentés par le symbole "+" dans le diagramme ci-dessous :

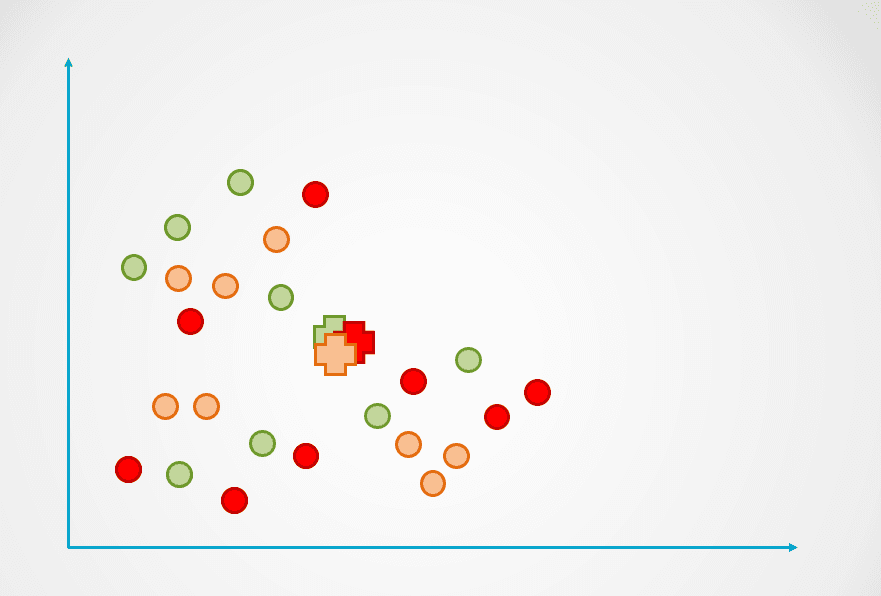
Image de l'auteur

Étape 2: Ensuite, la distance entre chaque point de données et le centroïde est mesurée et chaque point est assigné au centroïde le plus proche :

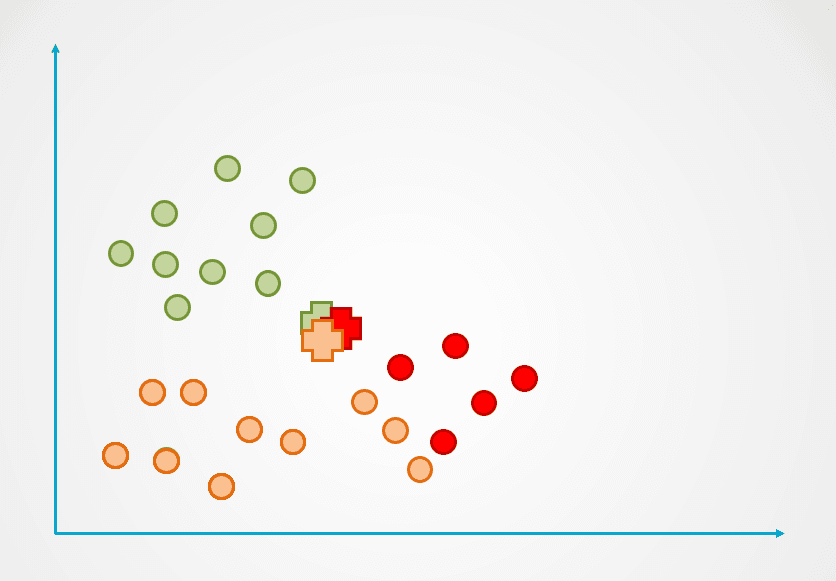
Image de l'auteur

Étape 3: Le centroïde du nouveau groupe est alors recalculé et les points de données sont réaffectés en conséquence.

Étape 4: Ce processus est répété jusqu'à ce que les points de données ne soient plus réaffectés :

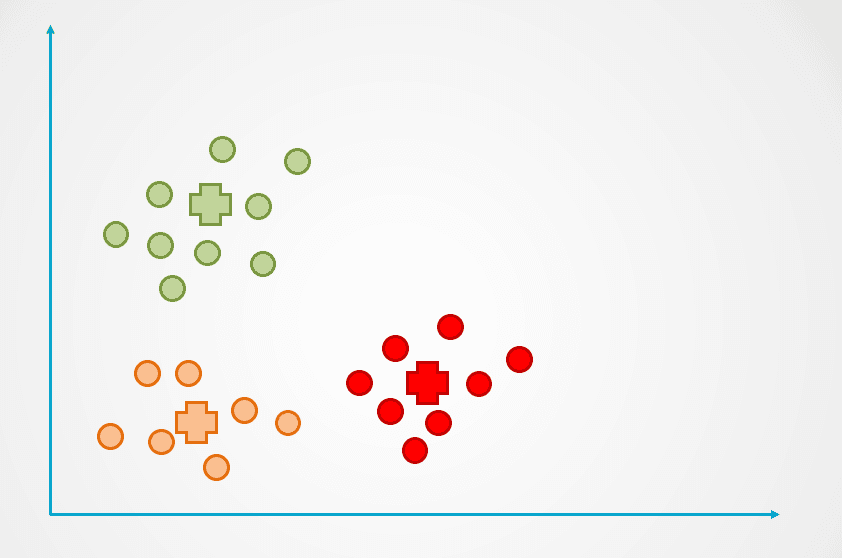
Image de l'auteur

Observez que trois groupes ont été créés dans l'exemple ci-dessus. Le nombre de grappes est appelé "k" dans l'algorithme de regroupement K-Means et doit être déterminé par nos soins.

Il existe plusieurs façons de sélectionner "k" dans K-Means, la plus populaire étant la méthode du coude. Cette technique consiste à tracer sur un graphique l'erreur pour un nombre différent de clusters et à choisir le point d'inflexion de la courbe comme "k". 

En savoir plus dans notre tutoriel sur le clustering K-Means en Python pour découvrir la méthode du coude et les rouages du clustering K-Means.

Construire un modèle de clustering K-Means en Python

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3, init='k-means++')

L'argument n_clusters indique le nombre de clusters "k" que vous devez définir lors de la construction de l'algorithme.

Explication des modèles d'apprentissage automatique - Prochaines étapes :

Si vous avez réussi à suivre l'intégralité de cet article, félicitations ! Vous connaissez maintenant certains des modèles et algorithmes d'apprentissage automatique supervisé et non supervisé les plus populaires et savez comment ils peuvent être appliqués pour résoudre divers problèmes de modélisation prédictive.

Pour devenir data scientist, vous devez comprendre comment fonctionnent les différents types de modèles d'apprentissage automatique afin de les appliquer à la résolution d'un problème. Par exemple, si vous souhaitez construire un modèle interprétable et à faible temps de calcul, il peut être judicieux de créer un arbre de décision. Toutefois, si votre objectif est de créer un modèle qui se généralise bien, vous pouvez choisir de construire un algorithme de forêt aléatoire.

Il est également important de comprendre comment évaluer les modèles d'apprentissage automatique. Un "bon" modèle est subjectif et dépend fortement de votre cas d'utilisation. Dans les problèmes de classification, par exemple, une grande précision n'est pas à elle seule le signe d'un bon modèle. En tant que scientifique des données, vous devez examiner des mesures telles que la précision, le rappel et le score F1 pour avoir une meilleure idée de la performance de votre modèle.

Si vous souhaitez acquérir une compréhension plus approfondie des modèles d'apprentissage automatique que les concepts abordés dans cet article, suivez la formation Machine Learning Scientist with Python. Ce parcours professionnel vous apprendra la théorie qui sous-tend le fonctionnement des modèles d'apprentissage automatique et la manière dont ils peuvent être mis en œuvre en Python. Vous apprendrez également des techniques de préparation des données telles que la normalisation, la décorrélation et la sélection des caractéristiques.