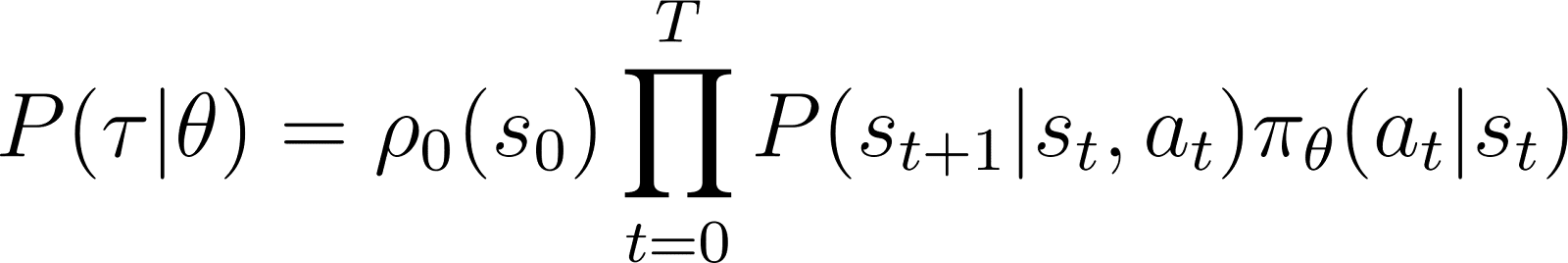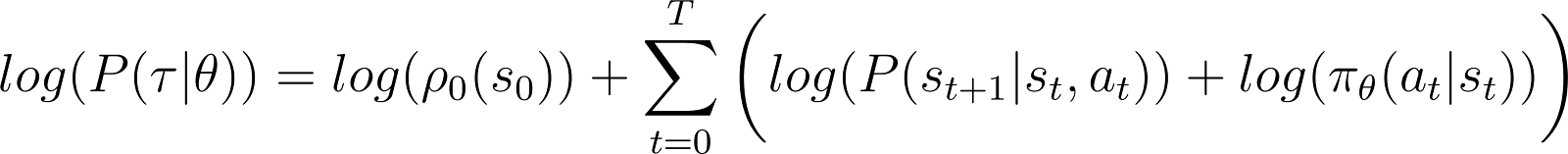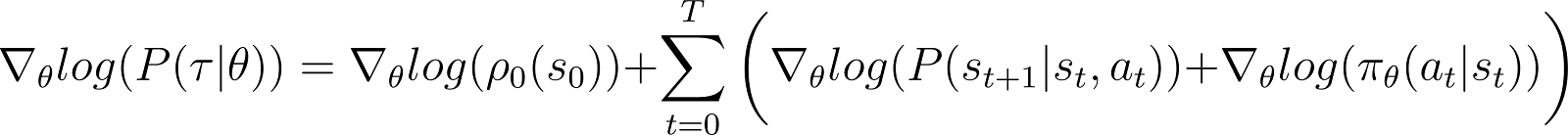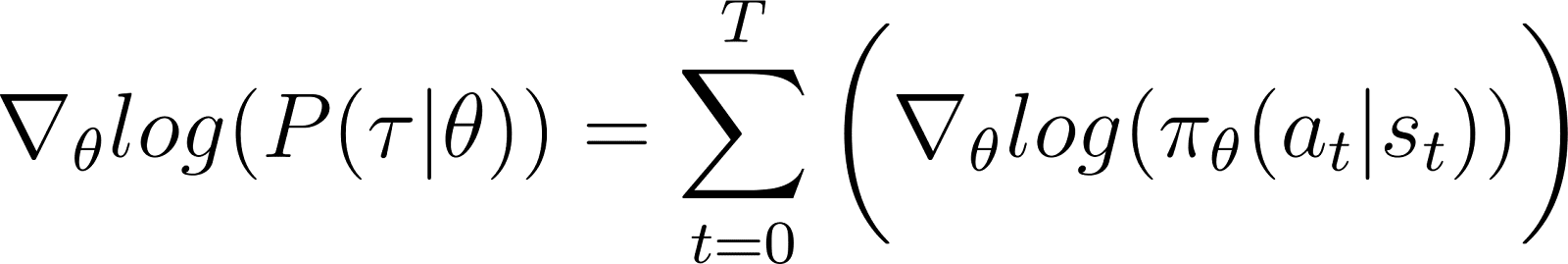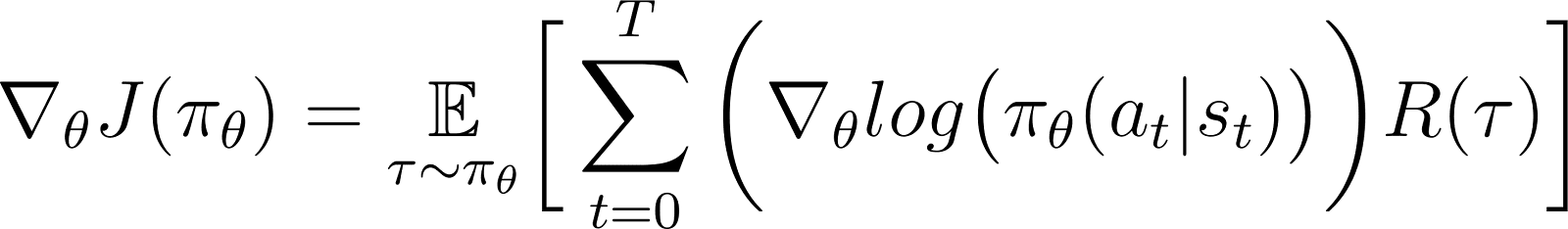Explicação do Teorema do Gradiente de Política: Uma introdução prática

Por que usar métodos de gradiente de política?

Uma das principais vantagens dos métodos de gradiente de política é sua capacidade de lidar com espaços de ação complexos, onde as abordagens tradicionais baseadas em valores têm dificuldades.

Manuseio de espaços de ação de alta dimensão

Os métodos baseados em valor, como o Q-learning, funcionam estimando a função de valor para todas as ações possíveis. Isso se torna difícil quando o espaço de ação do ambiente é contínuo ou discreto, mas grande. 

Os métodos de gradiente de política parametrizam a política e estimam o gradiente das recompensas cumulativas com relação aosparâmetros da política. Eles usam esse gradiente para otimizar diretamente a política, atualizando seus parâmetros. Portanto, eles podem lidar com eficiência com espaços de ação contínuos ou de alta dimensão. Os gradientes de política também são a base dos métodos de aprendizagem por reforço usando feedback humano (RLHF). 

Ao parametrizar a política e ajustar seus parâmetros com base em gradientes, os gradientes de política podem lidar com eficiência com ações contínuas e de alta dimensão. Essa abordagem direta permite uma melhor generalização e uma exploração mais flexível, tornando-a adequada para tarefas como controle robótico e outros ambientes complexos.

Aprendizado de políticas estocásticas

Dado um conjunto de observações: 

• Uma política determinística especifica a ação que o agente executa. 
• Uma política estocástica fornece um conjunto de ações e a probabilidade de o agente escolher cada ação. 

Ao seguir uma política estocástica, a mesma observação pode levar à escolha de diferentes ações em diferentes iterações. Isso promove a exploração do espaço de ação e evita que a política fique presa em ótimos locais. Por esse motivo, as políticas estocásticas são úteis em ambientes em que a exploração é essencial para descobrir o caminho que leva ao retorno máximo. 

Nos métodos baseados em políticas, o resultado da política é convertido em uma distribuição de probabilidade, com uma probabilidade atribuída a cada ação possível. O agente escolhe uma ação por amostragem dessa distribuição, o que possibilita a implementação de uma política estocástica. Assim, os métodos de gradiente de política combinam a exploração com o aproveitamento, o que é útil em ambientes com estruturas de recompensa complexas. 

Derivação do teorema do gradiente de política

Antes de mergulhar na derivação, é importante estabelecer a notação matemática e os principais conceitos usados na prova.

Notação matemática e preliminares

Conforme mencionado na seção anterior, o teorema do gradiente de política afirma que a derivada do retorno esperado é a expectativa do produto do retorno e a derivada do logaritmo da política. 

Antes de derivar o teorema do gradiente de política, apresentamos a notação:

• E[X] refere-se à expectativa probabilística de uma variável aleatória X.
• Matematicamente, a política é expressa como uma matriz de probabilidade que fornece a probabilidade de escolher diferentes ações com base em diferentes observações. Normalmente, uma política é modelada como uma função parametrizada, com os parâmetros representados como θ.
• _πθ refere-se a uma política parametrizada por θ. Na prática, esses parâmetros são os pesos da rede neural que modela a política. 
• A trajetória, τrefere-se a uma sequência de estados, normalmente partindo de um estado inicial aleatório até o intervalo de tempo atual ou o estado terminal.
• ∇_θf refere-se ao gradiente de uma função f com relação ao(s) parâmetro(s) θ.
• J(π_θ) refere-se ao retorno esperado obtido pelo agente seguindo a política _πθ. Essa também é a função objetiva para a subida do gradiente. 
• O ambiente oferece uma recompensa a cada etapa do tempo, dependendo da ação do agente. O retorno refere-se às recompensas cumulativas desde o estado inicial até o intervalo de tempo atual. 
• R(τ) refere-se ao retorno gerado ao longo da trajetória τ.

Etapas de derivação

Mostramos como derivar e provar o teorema do gradiente de política a partir dos primeiros princípios, começando com a expansão da função objetiva e usando o truque do derivado logarítmico. 

A função objetiva (Equação 1)

A função objetiva no método de gradiente de política é o retorno 

J acumulado ao seguir a trajetória com base na política π expressa em termos de parâmetros θ. Essa função objetiva é dada como: 

Na equação acima: 

• O lado esquerdo (LHS) é o retorno esperado obtido ao seguir a política π_θ.
• O lado direito (RHS) é a expectativa (sobre a trajetória τ gerada ao seguir a política π_θ em cada etapa) dos retornos R(τ) gerados na trajetória τ.

O diferencial da função objetiva (Equação 2)

Diferenciando (com relação a θ) ambos os lados da equação acima, você obtém:

O gradiente da expectativa (Equação 3)

A expectativa (no RHS) pode ser expressa como uma integral sobre o produto de: 

• A probabilidade de seguir uma trajetória τ
• Os retornos gerados ao longo da trajetória τ

Assim, o RHS da Equação 2 é reformulado como: 

O gradiente de uma integral é igual à integral do gradiente. Portanto, na expressão acima, podemos trazer o gradiente ∇_θ sob o sinal de integral. Portanto, o RHS se torna: 

Assim, a Equação 2 pode ser reescrita como:

A probabilidade da trajetória (Equação 4)

Agora, vamos dar uma olhada mais de perto em P(τ|θ), a probabilidade de o agente seguir a trajetória τ com base nos parâmetros de política θ (e, portanto, na política _πθ). Uma trajetória consiste em um conjunto de etapas. Assim: 

• A probabilidade de obter a trajetória τ é o produto de:
• A probabilidade de você seguir todas as etapas individuais. 

• Na etapa de tempo to agente passa do estado s para o estado s_t+1 seguindo a ação a_t. A probabilidade de isso acontecer é dada pelo produto de:
• A probabilidade de a política prever a ação a_t no estado s_t
• A probabilidade de você terminar no estado s_t+1 dada a ação a_t e estado s_t

Assim, partindo de um estado inicial s₀a probabilidade de o agente seguir a trajetória τ com base na política π_θ é dada como:

Para simplificar as coisas, queremos expressar o produto no RHS acima como uma soma. Portanto, tomamos o logaritmo de ambos os lados da equação acima:

A derivada da probabilidade logarítmica (Equação 5) 

Agora, tomamos a derivada (com relação a θ) da probabilidade de log na equação acima.

No RHS da equação acima: 

• O primeiro termo log ρ₀(s₀) é constante com relação a θ. Portanto, sua derivada é 0. 
• O primeiro termo dentro do somatório P(s_t+1|s_t, a_t) também é independente de θ e sua derivada com relação a θ também é 0.

Removendo os termos zero acima da equação, ficamos com a (Equação 5): 

Lembre-se de que, na Equação 2, você sabe que: 

A Equação 5 avalia o logaritmo da primeira parte do RHS da Equação 2. Precisamos relacionar a derivada de um termo com seu logaritmo. Fazemos isso usando a regra da cadeia e o truque da derivada do logaritmo. 

O truque da derivada de logaritmo

Fazemos um desvio e usamos as regras de cálculo para obter um resultado, que usaremos para simplificar a equação anterior e torná-la adequada para métodos computacionais. 

No cálculo, a derivada de um logaritmo pode ser expressa como: 

Assim, ao reorganizar a equação acima, a derivada de x pode ser expressa em termos da derivada do logaritmo de x:

Isso às vezes é chamado de truque da derivada do logaritmo. 

A regra da cadeia

De acordo com a regra da cadeia, dado z(y) como uma função de yonde y é uma função de θ, y(θ), a derivada de z em relação a θ é dada como:

Nesse caso, y(θ) representa P(θ) e z(y) representa log(y). Assim, 

Aplicação da regra da cadeia

Você sabe, pelo cálculo, que d(log(y)) / dy = 1/y. Use isso na primeira expressão do RHS acima. 

Mover y para o LHS e use a notação notação:

y representa P(θ). Portanto, a equação acima é equivalente a: 

Aplicando o truque da derivada de logaritmo

O resultado acima fornece a primeira expressão do RHS da Equação 2 (mostrada abaixo).  

Usando o resultado no RHS da Equação 2, obtemos: 

Reorganizamos os termos sob a integral RHS conforme abaixo:

Derivação do resultado final

Observe que a expressão acima contém a expansão integral de uma expectativa: ∫P(θ)∇logP(θ) = E[∇logP(θ)]

Assim, o RHS acima pode ser expresso como a expectativa: 

Substituímos a derivada da probabilidade logarítmica na expressão da recompensa esperada: 

Na equação acima, substitua o valor de ∇logP(θ) da Equação 5 para obter:

Essa é a expressão para o gradiente da função de recompensa de acordo com o teorema do gradiente de política. 

A intuição por trás do gradiente de política

Os métodos de gradiente de política convertem o resultado da política em uma distribuição de probabilidade. O agente coleta amostras dessa distribuição para escolher uma ação. Os métodos de gradiente de política ajustam os parâmetros da política. Isso leva à atualização dessa distribuição de probabilidade em cada iteração. A distribuição de probabilidade atualizada tem uma probabilidade maior de escolher ações que levam a recompensas maiores. 

O algoritmo de gradiente de política calcula o gradiente do retorno esperado em relação aos parâmetros da política. Ao mover os parâmetros da política na direção desse gradiente, o agente aumenta a probabilidade de escolher ações que resultem em recompensas mais altas durante o treinamento. 

Essencialmente, as ações que levaram a melhores resultados têm maior probabilidade de serem escolhidas no futuro, melhorando gradualmente a política para maximizar as recompensas de longo prazo.

Implementação de gradientes de política em Python

Depois de discutir os princípios fundamentais dos gradientes de política, mostramos como implementá-los usando o PyTorch e o Gymnasium. 

Configuração do ambiente

Como primeira etapa, precisamos instalar o gymnasium e algumas bibliotecas de suporte, como NumPy e PyTorch.

Para instalar o gymnasium e suas dependências em um servidor ou máquina local, execute:

$ pip install gymnasium 

Para instalar usando um Notebook como o Google Colab ou o DataLab, use: 

!pip install gymnasium

Você importa esses pacotes no ambiente Python:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.distributions as distributions
import numpy as np
import gymnasium as gym  

Codificação de um agente de gradiente de política simples

Crie uma instância do ambiente usando o método .make().

env = gym.make('CartPole-v1')

Assim como em outros métodos de aprendizado de máquina, usamos uma rede neural para implementar o agente de gradiente de política. 

O CartPole-v1 é um ambiente simples, portanto, projetamos uma rede simples com uma camada oculta com 64 neurônios. A dimensão da camada de entrada é igual às dimensões do espaço de observação. A dimensão da camada de saída é igual ao tamanho do espaço de ação do ambiente. Assim, a rede de políticas mapeia estados observados para ações. Com uma observação como entrada, a rede gera a ação prevista de acordo com a política. 

O código abaixo implementa a rede de políticas: 

class PolicyNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout):
        super().__init__()

        self.layer1 = nn.Linear(input_dim, hidden_dim)
        self.layer2 = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        x = self.layer1(x)
        x = self.dropout(x)
        x = F.relu(x)
        x = self.layer2(x)
        return x

Treinamento do agente

O ambiente dá uma recompensa em cada etapa do tempo, dependendo do estado e da ação do agente. A abordagem de gradiente de política consiste em executar a descida de gradiente nas recompensas cumulativas (retorno). O objetivo é maximizar o retorno total. 

Para calcular o retorno em um episódio, você acumula (com um fator de desconto) as recompensas de todas as etapas de tempo nesse episódio. Além disso, a normalização dos retornos é útil para garantir um treinamento suave e estável. O código abaixo mostra como você pode fazer isso:

def calculate_stepwise_returns(rewards, discount_factor):
    returns = []
    R = 0

    for r in reversed(rewards):
        R = r + R * discount_factor
        returns.insert(0, R)
    returns = torch.tensor(returns)
    normalized_returns = (returns - returns.mean()) / returns.std()
    return normalized_returns

Em cada iteração da passagem para frente, executamos as seguintes etapas: 

• Execute o agente com base na política atual usando a função .step(). A política prevê a probabilidade de você tomar a ação escolhida em cada etapa do tempo.
• Receber a recompensa do ambiente com base na ação do agente.
• Acumule as recompensas em etapas e as probabilidades de registro das ações até que o agente atinja um estado terminal.

O código abaixo implementa o passe para frente:

def forward_pass(env, policy, discount_factor):
    log_prob_actions = []
    rewards = []
    done = False
    episode_return = 0

    policy.train()
    observation, info = env.reset()

    while not done:
        observation = torch.FloatTensor(observation).unsqueeze(0)
        action_pred = policy(observation)
        action_prob = F.softmax(action_pred, dim = -1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)

        observation, reward, terminated, truncated, info = env.step(action.item())
        done = terminated or truncated

        log_prob_actions.append(log_prob_action)
        rewards.append(reward)
        episode_return += reward

    log_prob_actions = torch.cat(log_prob_actions)
    stepwise_returns = calculate_stepwise_returns(rewards, discount_factor)

    return episode_return, stepwise_returns, log_prob_actions

Usando backpropagation e gradient ascent para atualizar a política

No aprendizado de máquina tradicional:

• A perda refere-se à diferença entre a saída prevista e a real. 
• Minimizamos a perda usando a descida de gradiente.

In RL:

• A perda é um indicador da quantidade na qual a descida (ou subida) do gradiente deve ser aplicada. 
• Maximizamos o retorno (recompensas cumulativas) usando a subida do gradiente.
• O valor de retorno esperado é usado como um substituto para a perda de descida de gradiente. O valor de retorno esperado é o produto de:
• Os retornos esperados de cada etapa com 
• A probabilidade de você escolher a ação amostrada em cada etapa. 
• Para aplicar a subida do gradiente usando a retropropagação, usamos o negativo da perda. 

O código abaixo calcula a perda:

def calculate_loss(stepwise_returns, log_prob_actions):
    loss = -(stepwise_returns * log_prob_actions).sum()
    return loss

Semelhante aos algoritmos padrão de aprendizado de máquina, para atualizar a política, você executa a retropropagação em relação à função de perda. O método update_policy() abaixo invoca o método calculate_loss(). Em seguida, ele executa a retropropagação nessa perda para atualizar os parâmetros da política, ou seja, os pesos do modelo da rede de políticas. 

def update_policy(stepwise_returns, log_prob_actions, optimizer):
    stepwise_returns = stepwise_returns.detach()
    loss = calculate_loss(stepwise_returns, log_prob_actions)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss.item()

O ciclo de treinamento 

Usamos as funções definidas anteriormente para treinar a política. Antes de iniciar o treinamento, você precisa: 

• Uma política não treinada inicializada como uma instância aleatória da classe PolicyNetwork. 
• Um otimizador que usa o algoritmo Adam. 
• Hiperparâmetros para o fator de desconto, a taxa de aprendizado, a taxa de abandono, o limite de recompensa e o número máximo de épocas de treinamento. 

Nós repetimos o loop de treinamento até que o retorno médio exceda o limite de recompensa. Em cada iteração, executamos as seguintes etapas: 

• Para cada episódio, execute a passagem para frente uma vez. Colete a probabilidade logarítmica das ações, os retornos por etapas e o retorno total desse episódio. Acumule os retornos episódicos em uma matriz. 
• Calcule a perda usando as probabilidades de log e os retornos por etapas. Execute o backpropagation na perda. Use o otimizador para atualizar os parâmetros da política. 
• Verifique se o retorno médio em N_TRIALS excede o limite de recompensa .

O código abaixo implementa essas etapas:

def main(): 
    MAX_EPOCHS = 500
    DISCOUNT_FACTOR = 0.99
    N_TRIALS = 25
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    INPUT_DIM = env.observation_space.shape[0]
    HIDDEN_DIM = 128
    OUTPUT_DIM = env.action_space.n
    DROPOUT = 0.5

    episode_returns = []

    policy = PolicyNetwork(INPUT_DIM, HIDDEN_DIM, OUTPUT_DIM, DROPOUT)

    LEARNING_RATE = 0.01
    optimizer = optim.Adam(policy.parameters(), lr = LEARNING_RATE)

    for episode in range(1, MAX_EPOCHS+1):
        episode_return, stepwise_returns, log_prob_actions = forward_pass(env, policy, DISCOUNT_FACTOR)
        _ = update_policy(stepwise_returns, log_prob_actions, optimizer)

        episode_returns.append(episode_return)
        mean_episode_return = np.mean(episode_returns[-N_TRIALS:])

        if episode % PRINT_INTERVAL == 0:
            print(f'| Episode: {episode:3} | Mean Rewards: {mean_episode_return:5.1f} |')

        if mean_episode_return >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break

Execute o programa de treinamento chamando a função main():

main()

Esta pasta de trabalho do DataLab contémnha a implementação acima do algoritmo de gradiente de política. Você pode executá-lo diretamente ou usá-lo como ponto de partida para modificar o algoritmo.

Vantagens e desafios dos métodos de gradiente de política

Os métodos de gradiente de política oferecem várias vantagens, como:

• Manuseio de espaços de ação contínua: Os métodos baseados em valores (como o Q-learning) são ineficientes com espaços de ação contínuos porque precisam estimar valores em todo o espaço de ação. Os métodos de gradiente de política podem otimizar diretamente a política usando o gradiente dos retornos esperados. Essa abordagem funciona bem com distribuições de ações contínuas. Assim, os métodos de gradiente de política são adequados para tarefas como o controle robótico, que se baseia em espaços de ação contínuos.
• Políticas estocásticas: Os métodos de gradiente de política podem aprender políticas estocásticas, que fornecem uma probabilidade de seleção de cada ação possível. Isso permite que o agente experimente uma variedade de ações e reduz o risco de ficar preso em ótimos locais. Ele ajuda em ambientes complexos em que o agente precisa explorar o espaço de ação para encontrar a política ideal. A natureza estocástica ajuda a equilibrar a exploração (tentar novas ações) e o aproveitamento (escolher as ações mais conhecidas), o que é fundamental para ambientes com incerteza ou recompensas esparsas.
• Otimização direta de políticas: Os gradientes de política otimizam a política diretamente em vez de usar funções de valor. Em espaços de ação contínuos ou de alta dimensão, a aproximação de valores para cada ação pode se tornar computacionalmente cara. Assim, os métodos baseados em políticas têm bom desempenho nesses ambientes. 

Apesar de suas muitas vantagens, os métodos de gradiente de política têm alguns desafios inerentes:

• Alta variação nas estimativas de gradiente: Os métodos de gradiente de política selecionam ações por meio da amostragem de uma distribuição de probabilidade. Na verdade, eles fazem uma amostragem da trajetória para estimar o retorno esperado. Como o processo de amostragem é inerentemente aleatório, os retornos estimados nas iterações subsequentes podem ter alta variação. Isso pode dificultar o aprendizado eficiente do agente, pois as atualizações da política podem flutuar significativamente entre as iterações. 
• Instabilidade durante o treinamento:
• Os métodos de gradiente de política são sensíveis a hiperparâmetros como o. Se a taxa de aprendizado for muito alta, as atualizações dos parâmetros da política podem ser muito grandes, fazendo com que o treinamento não atinja os parâmetros ideais. Por outro lado, se a taxa de aprendizado for muito pequena, a convergência pode ser lenta. 
• Os métodos de gradiente de política precisam equilibrar a exploração e o aproveitamento. Se o agente não explorar o suficiente, ele poderá não alcançar a vizinhança da política ideal. Por outro lado, se ele explorar demais, não convergirá para a política ideal e oscilará no espaço de ação. 
• Ineficiência da amostra: Os métodos de gradiente de política estimam o retorno seguindo cada política até o término e acumulando as recompensas de cada etapa. Assim, eles precisam de muitas interações com o ambiente para desenhar um grande número de trajetórias de amostra. Isso é ineficiente e caro para ambientes com grandes espaços de estado ou de ação. 

Soluções para estabilidade

Como a instabilidade é um problema relativamente comum nos métodos de gradiente de política, os desenvolvedores adotaram várias soluções para estabilizar o processo de treinamento. A seguir, apresentamos soluções comuns para estabilizar o treinamento usando gradientes de política: 

Uso de funções de linha de base

Devido à amostragem ineficiente, os gradientes dos retornos estimados durante as iterações de treinamento podem ter alta variação, tornando o treinamento instável e lento. Uma abordagem comum para reduzir a variação é usar funções de linha de base, como o método Advantage Actor-Critic (A2C). A ideia é usar um proxy (a função de vantagem) em vez do retorno estimado para a função objetiva. 

A vantagem é calculada como a diferença entre o retorno real da trajetória amostrada e o retorno esperado dado o estado inicial. Essa abordagem envolve o uso da função de valor como o valor esperado dos estados e dos pares estado-ação. Ao representar a perda como a diferença entre o retorno real e o retorno esperado em vez de apenas os retornos, o A2C reduz a variação na função de perda e, portanto, nos gradientes, tornando o treinamento mais estável. 

Usando a regularização de entropia

Em determinados ambientes, como aqueles com recompensas esparsas (apenas alguns estados dão uma recompensa), a política adota rapidamente uma abordagem determinística. Ele também adota uma abordagem gananciosa e explora os caminhos que já explorou. Isso impede uma exploração mais aprofundada e, muitas vezes, leva à convergência para ótimos locais e políticas abaixo do ideal. 

A solução é incentivar a exploração para penalizar a política quando ela se tornar muito determinista. Isso é feito adicionando um termo baseado em entropia à função objetiva. A entropia mede a quantidade de aleatoriedade na política. Quanto maior a entropia, maior a aleatoriedade nas ações escolhidas pelo agente. Esse termo baseado em entropia é o produto do coeficiente de entropia e da entropia da política atual. 

Tornar a entropia uma parte da função objetiva ajuda a alcançar um equilíbrio entre exploração e explotação. 

Extensões de gradiente de política

Entre as várias extensões dos métodos de gradiente de política, uma das mais fundamentais é o algoritmo REINFORCE. Ele fornece uma implementação direta do teorema do gradiente de política e é a base para técnicas mais avançadas.

Algoritmo REINFORCE

O algoritmo REINFORCE, também conhecido como Monte Carlo Reinforce, é uma das implementações básicas do teorema do gradiente de política. Ele usa métodos de Monte Carlo para estimar retornos e gradientes de política. Ao seguir o algoritmo REINFORCE, o agente coleta diretamente amostras de todas as ações (do estado inicial ao terminal) do ambiente. Isso contrasta com outros métodos, como o TD-Learning e a Programação Dinâmica, que utilizam bootstrap em suas ações com base em estimativas de função de valor. 

A seguir, apresentamos as etapas básicas do algoritmo REINFORCE:

• Inicialize a política com parâmetros aleatórios
• Repita vários episódios de treinamento. Para cada episódio: 
• Gere cada etapa de todo o episódio da seguinte forma: 
• Passe o estado para a função de política. 
• A função de política gera probabilidades para cada ação possível.
• Faça uma amostragem aleatória de uma ação dessa distribuição de probabilidade.
• Para cada estado do episódio, estime os retornos (recompensas cumulativas descontadas) até a etapa.
• Estimar o gradiente da função objetiva (de acordo com o teorema do gradiente da política), expresso como o produto dos retornos por etapas e as probabilidades de ação para cada etapa. 
• Atualize os parâmetros da política aplicando os gradientes

Para cada política, você pode fazer uma amostragem de uma única trajetória para estimar o gradiente (como mostrado acima) ou calcular a média do gradiente em várias trajetórias amostradas sob a mesma política. 

Métodos de crítica ao ator

Os métodos de crítica do ator combinam métodos de gradiente de política (como o REINFORCE) com funções de valor.

• O funcionamento do ator é semelhante aos métodos de gradiente de política. O ator implementa a política, selecionando ações em cada etapa com base na política. Ele atualiza a política seguindo o gradiente do retorno esperado. 
• O crítico implementa a função de valor, que é usada como linha de base (discutida na seção anterior). Isso ajuda a tornar o treinamento mais eficiente e estável. 

Os métodos de gradiente de política, como o REINFORCE, estimam os gradientes ao longo de cada trajetória usando o retorno bruto. Como um processo de amostragem desenha essas trajetórias, ele pode levar a grandes variações nos retornos e gradientes. O uso de uma função de vantagem em vez dos retornos brutos resolve esse problema. A função de vantagem é a diferença entre os retornos reais e os esperados (ou seja, a função de valor). Os métodos críticos de ator são uma classe de algoritmos. Quando o crítico é implementado usando a função de vantagem (a abordagem mais comum), ele também é chamado de Advantage actor-critic (A2C). 

Otimização da política proximal (PPO)

Em ambientes complexos, os métodos críticos de atores, como o A2C, não são suficientes para controlar a variação nos retornos e gradientes. Nesses casos, restringir artificialmente o valor pelo qual a política pode mudar em cada iteração ajuda. Isso força a política atualizada (após a subida do gradiente) a ficar na vizinhança da política antiga. 

Métodos como o Proximal Policy Optimization fazem duas modificações nos gradientes de política:

• Use uma função de vantagem. Normalmente, essa função de vantagem usa a função de valor como linha de base. Nesse aspecto, eles são semelhantes aos métodos A2C. 
• Restringir o valor pelo qual os parâmetros da política podem mudar em cada iteração. Isso é feito usando uma função objetiva substituta recortada. O algoritmo especifica um intervalo dentro do qual a proporção da nova política em relação à política antiga deve estar. Quando a proporção (após a atualização do gradiente) excede esses valores predeterminados, ela é cortada para ficar dentro do intervalo. 

Assim, o PPO melhora significativamente os métodos de gradiente de política vanilla, o que aumenta a estabilidade em ambientes complexos. A função objetiva recortada evita que grandes variações nos retornos e gradientes desestabilizem as atualizações da política. Para obter um equilíbrio entre a exploração e o aproveitamento, também é possível modificar o PPO para usar a regularização de entropia. Isso é feito adicionando um termo de entropia (um parâmetro de escala multiplicado pela entropia da política) à função objetiva. 

Avanços recentes

Os gradientes de política estão entre os primeiros métodos usados para resolver problemas de RL. Após o advento das GPUs rápidas, várias novas abordagens foram propostas para aplicar técnicas modernas de ML a gradientes de políticas. 

Aprendizado por reforço com reforço gradiente 

Nos últimos anos, houve progresso na aplicação de métodos como o aumento do gradiente aos algoritmos de RL. O Gradient boosting combina as previsões de vários modelos fracos para gerar um único modelo forte. Isso é chamado de Aprendizado por Reforço com Impulso Gradiente (GBRL). O GBRL é um pacote Python semelhante ao XGBoost que implementa essas técnicas para algoritmos de RL.

Transferência de aprendizado por reforço 

A aprendizagem por transferência (TL) é uma técnica em que o conhecimento adquirido por um modelo é aplicado para melhorar o desempenho de outro modelo. A aprendizagem por transferência é útil porque treinar modelos de ML do zero é caro. As abordagens de TL foram usadas com gradientes de política para melhorar o desempenho dos modelos de RL. Essa abordagem é chamada de Aprendizado por Reforço de Transferência (TRL). 

Conclusão

Os gradientes de política estão entre as abordagens mais fundamentais para resolver problemas de RL.

 Neste artigo, apresentamos os primeiros princípios dos gradientes de política e mostramos como derivar o teorema do gradiente de política. Também demonstramos como implementar um algoritmo simples baseado em gradiente usando o PyTorch em um ambiente Gymnasium. Por fim, discutimos os desafios práticos e as extensões comuns do algoritmo básico de gradiente de política.

Se você quiser aprofundar seu conhecimento sobre aprendizagem por reforço e aprendizagem profunda com o PyTorch, confira estes cursos:

• Trilha de Aprendizagem por Reforço - Aprenda os fundamentos da RL, desde métodos baseados em valores até técnicas de otimização de políticas.
• Introdução à aprendizagem profunda com PyTorch - Obtenha experiência prática com o PyTorch e crie modelos de aprendizagem profunda a partir do zero.