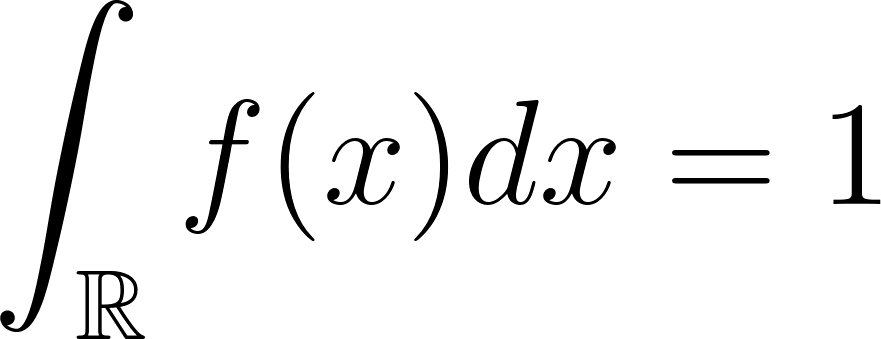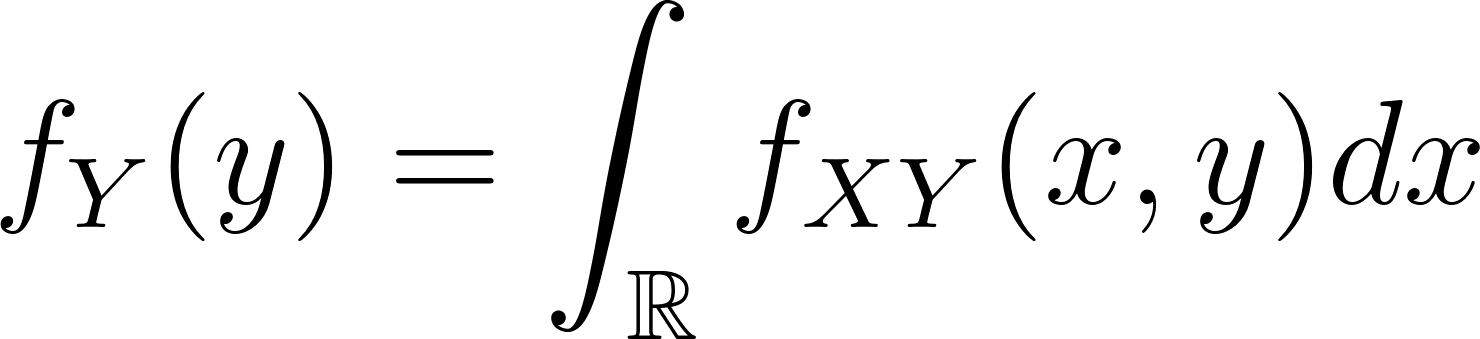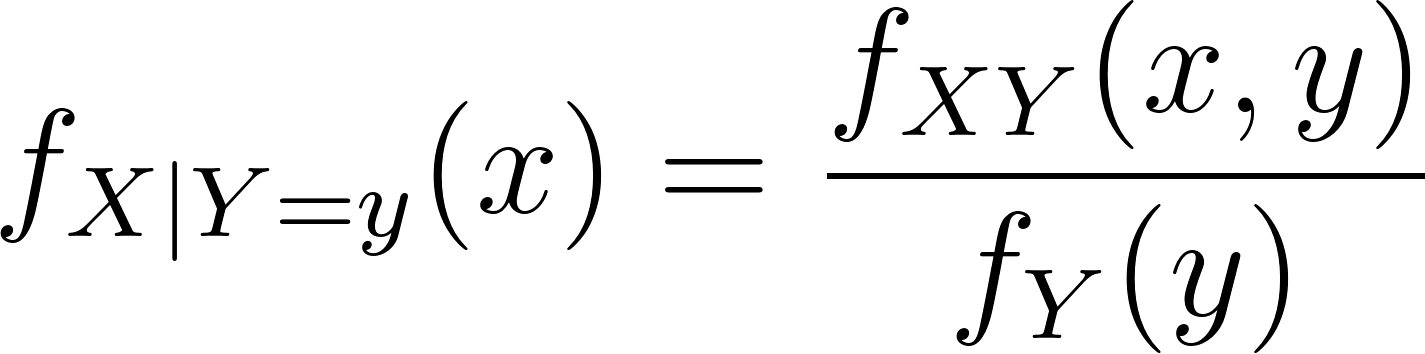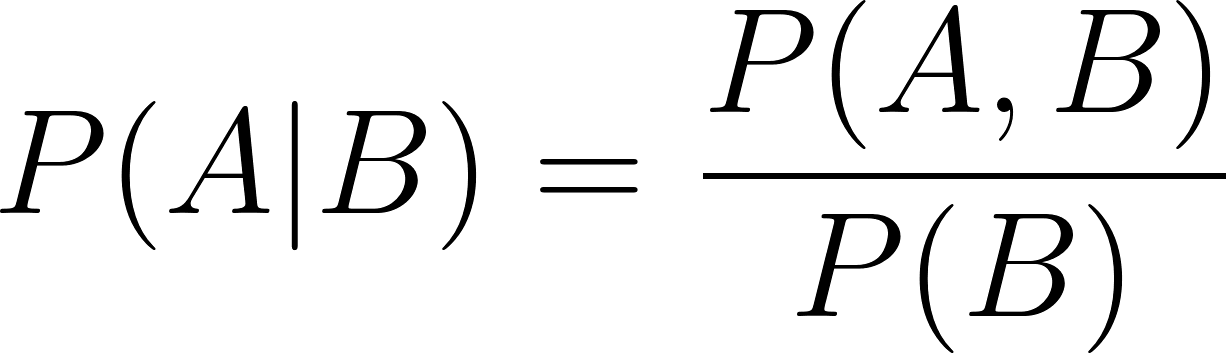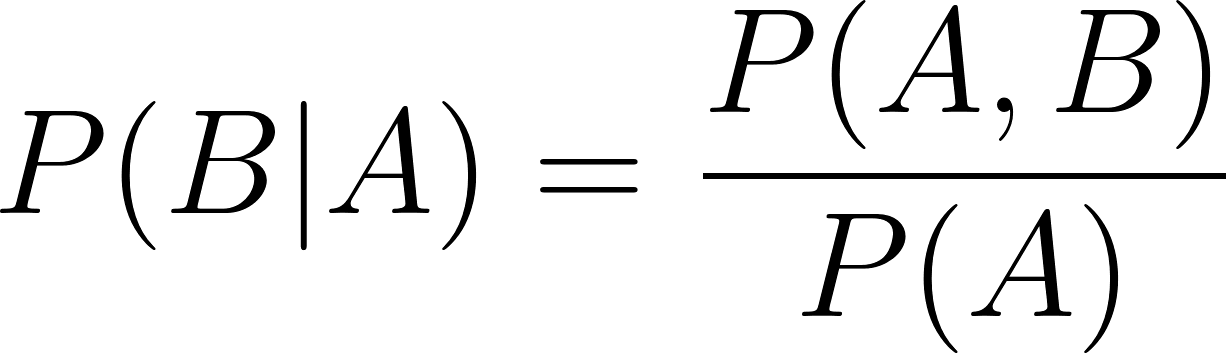Curso
Os modelos de machine learning (ML) são implementações baseadas em computador de métodos estatísticos e probabilísticos. Em geral, eles adotam uma de duas abordagens: modelagem generativa ou discriminativa.
Neste artigo, fornecemos uma visão geral dos modelos generativos e discriminativos, apresentamos modelos comuns de cada tipo, explicamos os princípios matemáticos por trás de ambas as abordagens e discutimos exemplos práticos dos tipos de problemas para os quais cada tipo de modelo pode ser usado.
O que são modelos generativos?
Dadoum conjunto de pontos de dados de exemplo, D, e seus rótulos associados, L, um modelo generativo aprende a distribuição de probabilidade conjunta P(D, L). Em seguida, ele usa essa distribuição subjacente para gerar novos dados semelhantes aos exemplos de treinamento ou resolver problemas de classificação.
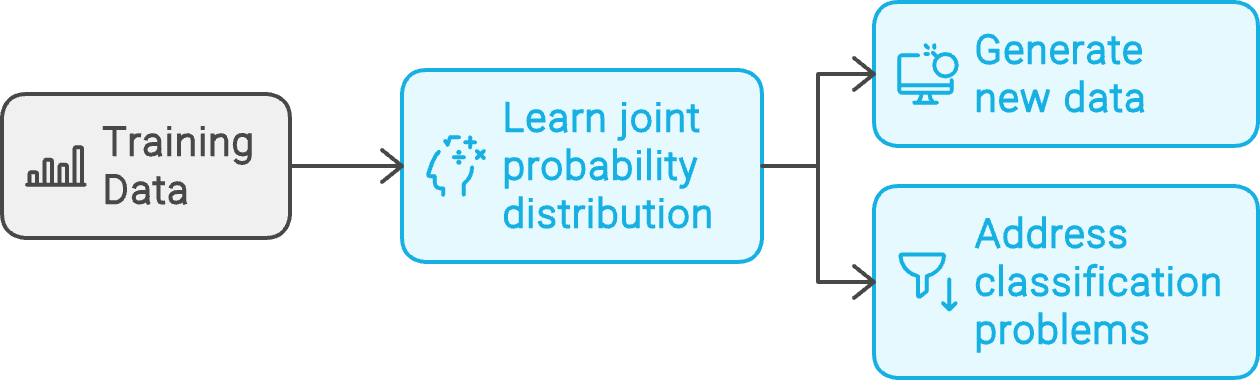
Fluxo de trabalho do modelo generativo. Criado com napkin.ai
As seções a seguir explicam os fundamentos dos modelos generativos com exemplos.
Modelos Naive Bayes
Os modelos Naive Bayes são baseados no teorema de Bayes. Esse teorema fornece a probabilidade condicional P(A | B) de um evento A quando se sabe que o evento B é verdadeiro. Isso é chamado de probabilidade posterior de A dado B.
Individualmente, a probabilidade P(A) do evento A é chamada de probabilidade prévia. Os modelos Naive Bayes pressupõem que A e B são eventos independentes - daí o prefixo "naive" (ingênuo). Se A e B forem dependentes, o teorema tradicional de Bayes não se aplica mais, e os modelos Naive Bayes não são a escolha certa.
Os modelos bayesianos são modelos generativos porque modelam a distribuição de probabilidade conjunta. O processo de treinamento aprende a probabilidade conjunta - P(A, B). Após o treinamento, ele pode ser usado para prever os valores de A com a maior probabilidade P(A). Além disso, os modelos bayesianos também podem ser usados para classificação porque podem calcular probabilidades condicionais (usando a regra de Bayes).
Para aprender a usar modelos naive Bayes na prática, siga o tutorial sobre como criar modelos Naive Bayes usando o scikit-learn e o Python.
Modelos de mistura gaussiana
Os modelos de mistura gaussiana (GMM) são uma classe de modelos de mistura. Sua premissa exclusiva é que os dados subjacentes combinam distribuições estatísticas em vez de uma única distribuição.
Em um GMM, presume-se que a população seja uma combinação de diferentes subpopulações, cada uma delas com uma distribuição gaussiana. Na verdade, a distribuição de dados é analisada como uma média ponderada de algumas distribuições gaussianas individuais.
Os GMMs capturam a distribuição de probabilidade do conjunto de dados subjacente. Assim, eles são usados para tarefas como análise de exceções e classificação não supervisionada. Essas tarefas envolvem a criação de um modelo estatístico da população, tratando o conjunto de dados de treinamento como uma amostra aleatória.
O curso sobre modelos de mistura no R aborda os detalhes práticos dos GMMs.
Redes adversárias generativas
Uma rede adversária generativa (GAN) é um modelo baseado em rede neural. Ele consiste em duas partes: um gerador e um discriminador. A rede do gerador é treinada para gerar vetores semelhantes aos exemplos de treinamento, enquanto o discriminador é treinado para distinguir entre os exemplos originais e os gerados pelo gerador.
Em essência, o gerador e o discriminador têm objetivos de treinamento opostos, o que os torna adversários. Por isso, a palavra "adversarial" é usada no nome.
O gerador e o discriminador são treinados juntos no mesmo loop de treinamento. À medida que o gerador se aprimora na criação de exemplos realistas, o discriminador distingue os exemplos originais dos gerados. O treinamento continua até que o gerador aprenda a gerar exemplos que sejam tão semelhantes aos dados de treinamento que o discriminador não consiga distinguir entre eles.
Após o treinamento, o gerador é usado para gerar dados sintéticos realistas semelhantes aos exemplos originais.
Modelos ocultos de Markov
Um modelo oculto de Markov (HMM) funciona com conjuntos de dados sequenciais. Os processos de Markov (ou cadeias de Markov) são usados para modelar dados sequenciais. A premissa de um modelo Markov é que o próximo elemento, xn+1na sequência depende apenas do elemento anterior, xne não de nenhum dos elementos, {x1, x2, ... xn-1}antes dele. Os modelos de Markov pressupõem que os conjuntos de dados sequenciais podem ser representados por processos de Markov com estados ocultos.
Esses estados geram o próximo elemento da sequência:
- A saída atual do modelo depende apenas do estado atual
- O estado atual depende apenas do estado anterior. A premissa dos modelos de Markov é que todas as informações relevantes do estado inicial até o (N-2)º estado são encapsuladas no (N-1)º estado. Não há necessidade de considerar explicitamente os estados anteriores.
Os modelos de Markov são representados com probabilidades de transição (ir de um estado para outro) e probabilidades de emissão (gerando um determinado elemento de sequência em um determinado estado).
Os HMMs modelam os conjuntos de dados de treinamento como processos de Markov. O objetivo do treinamento é determinar as probabilidades de transição e emissão para maximizar a probabilidade de gerar as sequências nos conjuntos de dados de exemplo. Assim, dada uma sequência, um modelo de Markov treinado pode gerar os elementos sucessivos da sequência.
Para saber mais sobre sua implementação prática, siga o tutorial sobre cadeias de Markov em Python.
O que são modelos discriminativos?
Dadoum conjunto de dados de treinamento que consiste em pontos de dados, D, e seus rótulos associados, L, um modelo discriminativo aprende a distribuição de probabilidade condicional P(D | L). Em seguida, ele usa essa distribuição de probabilidade condicional para prever a classe de novos pontos de dados.

Fluxo de trabalho do modelo discriminativo. Criado com napkin.ai
Os modelos discriminativos são geralmente usados para resolver problemas de classificação. Os exemplos a seguir demonstram seus casos de uso.
K-vizinhos mais próximos
O K-nearest neighbors (KNN) é um dos modelos mais antigos de machine learning. Ele se baseia na premissa de que, dada uma distribuição de pontos de dados, itens semelhantes estão localizados nas proximidades.
Os modelos KNN são não paramétricos, sem parâmetros como os coeficientes de regressão. Eles são usados para problemas de classificação e regressão.
A categoria de um ponto de dados de entrada é a mesma de seus k vizinhos mais próximos. O valor previsto de um ponto de dados é o valor médio de seus k vizinhos mais próximos. k (o número de vizinhos mais próximos a serem considerados) pode ser considerado um hiperparâmetro do modelo. Ele é usado para ajustar o comportamento do modelo, mas não afeta diretamente a saída do modelo.
Regressão logística
A regressão logística, assim como a regressão linear, tenta prever o valor de uma variável dependente com base em uma ou mais variáveis independentes. Na regressão linear, a variável dependente assume valores contínuos. Na regressão logística, a variável dependente assume valores discretos, como
- Verdadeiro e falso (regressão logística binária)
- Uma lista de categorias (regressão logística multinomial)
- Uma lista de valores ordenados, como um sistema de classificação baseado em letras - A, B, C, D, E, F (regressão logística ordinal)
A regressão linear prevê valores numéricos. Na regressão logística, a quantidade prevista é o logaritmo da razão de chances.
Para um evento A, com probabilidade P(A)a razão de chances é P(A) / (1 - P(A)). O uso do logaritmo (da razão de chances) leva a uma convergência mais suave e rápida durante o processo de treinamento. Devido à sua capacidade de segregar entradas em classes, os modelos logísticos são usados para fins de discriminação.
Para uma introdução mais prática a esse tópico, consulte o guia sobre regressão logística em Python.
Você também pode implementar a regressão logística usando o R, uma linguagem de programação orientada para estatísticas, conforme explicado no tutorial sobre regressão logística usando o R.
Máquinas de vetores de suporte (SVM)
As máquinas de vetores de suporte determinam a linha ideal que separa os pontos de dados de diferentes classes. No plano bidimensional X-Y, dada uma coleção de pontos de dados de duas categorias diferentes, o SVM prevê uma linha que (idealmente) separa claramente os pontos de uma categoria da outra.
Essa linha é o limite de decisão. Ele se torna um hiperplano para dados com três ou mais dimensões. Os pontos de dados (de qualquer categoria) que estão mais próximos dessa linha imaginária são chamados devetores de suporte do modelo . Esses pontos de dados são os mais difíceis de classificar, pois seus valores são próximos.
A distância entre a linha de separação e os vetores de suporte é chamada de margem. O treinamento do SVM visa encontrar o limite de decisão que maximiza essa margem. Na prática, os pontos de dados têm mais de duas dimensões, e a linha de separação é um hiperplano de dimensão superior.
Os SVMs também são usados para problemas de classificação multiclasse.
Para saber mais sobre SVMs, siga este guia sobre como criar SVMs usando o pacote Python scikit-learn. Além do Python, você também pode usar o R para implementar SVMs, conforme discutido neste guia sobre SVMs em R.
Árvores de decisão e florestas aleatórias
Uma árvore de decisão consiste em vários nós de decisão organizados em uma estrutura semelhante a uma árvore.
O nó mais alto é a raiz. Os nós que levam às saídas finais são chamados de nós folha ou terminais. Os nós intermediários não-folha são chamados de nós internos. A saída do nó raiz alimenta os nós intermediários. O resultado (saída) de cada nó é a saída final ou leva (ramifica) a outro nó.
Cada nó da árvore divide o conjunto de dados em um atributo específico. Por exemplo, uma árvore de decisão para aprovar solicitações de empréstimo pode ter nós para separar as solicitações por sua renda líquida.
O processo de treinamento determina o valor de limite apropriado para cada decisão. Por exemplo, solicitações com renda líquida abaixo de um determinado valor são totalmente rejeitadas. O restante é processado em nós subsequentes, que consideram outros atributos, como a riqueza líquida.
Para obter um guia prático sobre árvores de decisão, siga o tutorial sobre como criar árvores de decisão usando Python ou o curso completo sobre machine learning com modelos baseados em árvores em Python.
A principal desvantagem das árvores de decisão é o excesso de ajuste, o que leva a problemas de dados fora da amostra. As florestas de decisão tentam resolver esse problema. Uma floresta de decisões consiste em muitas árvores. Ao contrário das árvores de decisão autônomas, que devem considerar todo o conjunto de recursos, cada árvore em uma floresta encontra apenas um subconjunto aleatório do conjunto de recursos. Essa aleatoriedade ajuda a lidar com a variação em conjuntos de dados ruidosos.
A saída da floresta é obtida pela combinação, por exemplo, pela média, da saída de árvores individuais.
Para saber como implementar florestas aleatórias, consulte o guia sobre como usar o scikit-learn para criar classificadores de florestas aleatórias.
Redes neurais
Uma rede neural consiste em grupos de neurônios. Cada neurônio implementa uma função linear que multiplica os pesos do neurônio com o vetor de entrada.
Uma função de ativação não linear segue a função linear. A função de ativação decide a saída de cada neurônio com base na saída da função linear. Assim, uma rede neural simples pode ser conceitualmente vista como uma série de equações lineares filtradas por ativações não lineares.
A camada de entrada de uma rede neural multiplica a entrada (representada como um vetor) por um conjunto de pesos e funções de ativação. Essa saída é passada para a próxima camada, que executa uma operação semelhante.
As camadas ocultas estão entre a entrada e a saída camadas. A última camada oculta alimenta a camada de saída. Problemas complexos envolvem o uso de redes neurais com muitas camadas ocultas, que são chamadas de redes neurais profundas (DNNs).
Em um problema de classificação, uma abordagem comum é ter tantos neurônios de saída quanto o número de classes. A classe prevista corresponde ao neurônio com o valor mais alto. Em um problema de regressão, um único neurônio de saída contém a saída prevista. As relações lineares dos neurônios modelam a equação de regressão linear.
Para obter uma compreensão mais aprofundada do tópico, confira a postagem do blog sobre redes neurais.
Diferenças entre modelos generativos e discriminativos
Algumas tarefas, como a classificação, podem ser resolvidas usando qualquer tipo de modelo. Em geral, porém, os modelos discriminativos e generativos costumam ter casos de uso exclusivos, pois adotam abordagens matemáticas diferentes. É necessário entender essas diferenças e como elas afetam a adequação de cada categoria de modelos a vários problemas.
Abordagem para modelagem
Os modelos generativos preveem o próximo valor em uma sequência ou geram uma imagem com base em um texto (ou vice-versa). Para realizar essas tarefas, o modelo precisa aprender qual saída gerar com diferentes entradas. O modelo usa adistribuição de probabilidade conjunta da entrada e da saída .
Para entender a matemática subjacente, vamos começar com um exemplo simples. O comportamento de uma única variável aleatória é descrito por suafunção de densidade de probabilidade (PDF) .
A PDF da variável aleatória X pode ser usada para determinar a probabilidade de X em valores diferentes. Por exemplo, se a PDF de X for f(x)a probabilidade de X estar entre A e B é dada por :
A probabilidade de X em todo o intervalo é 1. Isso é expresso como :
A expressão acima também pode ser escrita como:
Para um PDF conjunto de duas variáveis, X e Ya integral sobre todo o intervalo é 1:
A distribuição de probabilidade conjunta mapeia todo o espaço de probabilidade de X e Y. Para avaliar a probabilidade de que a probabilidade conjunta P(X, Y) caia em uma região G, integre a PDF conjunta sobre G:
Em vez disso, os modelos discriminativos se concentram apenas na distribuição de probabilidade condicional. Os modelos generativos, se necessário, estimam a probabilidade condicional usando as probabilidades marginais.
Dada uma distribuição de probabilidade conjunta fXY(x,y)a probabilidade marginal da variável aleatória Y no valor y (para todos os valores de X) é dado como:
Semelhante à regra de Bayes, a PDF condicional de X é então expressa como:
A expressão acima mostra a versão integral da probabilidade condicional, que é mais comumente escrita como:
Da mesma forma,
Nas duas fórmulas de probabilidade condicional acima:
- O lado esquerdo (LHS) é a probabilidade condicional (as condicionais)
- O numerador do lado direito (RHS) é a probabilidade conjunta
- O denominador do RHS é a probabilidade marginal.
Para calcular uma probabilidade condicional, os modelos generativos seguem duas etapas:
- Estimando o PDF conjunto e os marginais.
- Avalie a expressão no lado direito da equação acima.
Por outro lado, os modelos discriminativos seguem uma única etapa (e mais simples):
- Estimar diretamente a probabilidade condicional (o lado esquerdo da equação) com base nos dados de treinamento.
Flexibilidade e complexidade
Um modelo generativo tem as marginais P(A) e P(B) e a PDF conjunta P(A, B). Com isso, você pode avaliar P(A | B) ou P(B | A) com a mesma facilidade. Essa é a ideia subjacente aos classificadores naive Bayes. Assim, os modelos generativos podem realizar tarefas como:
- Geração de novos exemplos usando a distribuição de probabilidade conjunta.
- Prever o rótulo mais relevante em um novo exemplo usando a probabilidade condicional.
- Prever o exemplo mais relevante com um novo rótulo usando a outra probabilidade condicional.
- Estimar a probabilidade geral de determinados eventos usando as probabilidades marginais.
Isso torna os modelos generativos flexíveis e multifuncionais. Por outro lado, elas envolvem inerentemente mais complexidade durante o treinamento, porque:
- O modelo precisa estimar as PDFs conjuntas e as PDFs marginais.
- Em seguida, se necessário, o modelo avalia as condicionais
Os modelos discriminativos, por outro lado, estão preocupados apenas com condicionais. Com base no conjunto de dados de treinamento, é possível estimar as probabilidades condicionais diretamente sem estimar as probabilidades conjuntas ou marginais.
Assim, os modelos discriminativos são mais simples de treinar. No entanto, um modelo discriminativo que tenha aprendido a probabilidade condicional P(A | B) só pode executar tarefas que envolvam essa probabilidade condicional específica. Ele não pode fazer mais nada.
Desempenho em tarefas de classificação
Os modelos generativos são suficientemente flexíveis para tarefas generativas e discriminativas. Durante o treinamento, o modelo aprende a PDF conjunta e os marginais. Durante a inferência, o modelo deve calcular a probabilidade condicional usando a distribuição conjunta e a probabilidade marginal apropriada. Portanto, a inferência em tarefas discriminativas é mais lenta.
Os modelos discriminativos, por outro lado, aprenderam diretamente (numericamente) as probabilidades condicionais. Eles estimam a probabilidade condicional em uma única etapa com base nos dados de entrada durante a inferência.
Além disso, como os modelos discriminativos se concentram apenas na estimativa de uma única quantidade (a probabilidade condicional), observa-se que eles são mais precisos. Uma PDF conjunta tem mais incerteza incorporada do que uma simples probabilidade condicional. Essa incerteza adicional se reflete na precisão relativamente menor dos modelos generativos para tarefas de classificação.
Modelos generativos versus modelos discriminativos: Um resumo
Com base na discussão das seções anteriores, a tabela abaixo resume as diferenças entre os modelos generativos e discriminativos.
|
Modelos generativos |
Modelos discriminativos |
|
|
Objetivo |
Capture a probabilidade conjunta e a probabilidade marginal. Use a regra de Bayes para calcular a probabilidade condicional. |
Capture apenas a probabilidade condicional. Não há informações sobre probabilidades conjuntas ou marginais. |
|
Geração de dados |
Pode gerar novos pontos de dados com base no conjunto de dados de treinamento. Por exemplo, um modelo treinado em dígitos manuscritos pode gerar dígitos novos e falsos. |
Não é possível gerar novos pontos de dados. Focado principalmente na distinção entre diferentes categorias de dados. |
|
Caso de uso principal |
Pode ser usado para tarefas generativas (por exemplo, síntese de dados) e tarefas discriminativas (por exemplo, classificação). |
Só pode ser usado para tarefas discriminativas, como classificação ou regressão. |
|
Desempenho da inferência |
A execução da inferência é mais lenta devido à necessidade de cálculos complexos. Até mesmo tarefas simples exigem o cálculo de probabilidades marginais e conjuntas e a aplicação da regra de Bayes. |
Inferência mais rápida porque calcula diretamente a probabilidade condicional sem envolver a regra de Bayes. |
|
Tratamento de dados ausentes |
Melhor no tratamento de dados ausentes por meio da modelagem da distribuição de probabilidade subjacente, facilitando o "preenchimento das lacunas". Menor risco de ajuste excessivo. |
Menos eficaz no tratamento de dados ausentes. Maior risco de sobreajuste porque o modelo se concentra em encontrar o hiperplano de separação entre as classes. |
|
Convergência |
Eles tendem a convergir mais rapidamente e com menos exemplos de treinamento, mas geralmente resultam em um erro de modelo mais alto, especialmente em tarefas de classificação, devido ao cálculo indireto da probabilidade condicional por meio da modelagem da distribuição de probabilidade conjunta. |
Em geral, eles exigem mais dados para serem treinados e podem convergir mais lentamente. No entanto, o resultado é um erro de modelo menor, especialmente em tarefas de classificação, porque eles modelam diretamente a probabilidade condicional sem estimar a distribuição de probabilidade conjunta. |
|
Complexidade do modelo |
Normalmente, eles são mais complexos porque modelam toda a distribuição de dados, incluindo as interações entre recursos e rótulos. |
Em geral, são mais diretos porque só precisam modelar o limite de decisão ou o hiperplano separado entre as classes. |
|
Exemplos de modelos |
Naive Bayes, modelos ocultos de Markov (HMMs), redes adversárias generativas (GANs), autoencodificadores variacionais (VAEs). |
Regressão logística, máquinas de vetor de suporte (SVMs), redes neurais e árvores de decisão. |
|
Flexibilidade do modelo |
Mais flexível em termos de aplicação (pode lidar com tarefas generativas e discriminativas). |
Menos flexível (limitado a tarefas discriminativas). |
|
Taxas de erro |
Taxas de erro mais altas em tarefas de classificação devido a métodos de estimativa indireta. |
Taxas de erro mais baixas em tarefas de classificação devido ao treinamento direto em probabilidade condicional. |
Quando usar modelos generativos
Como o nome sugere, os modelos generativos são especialmente adequados para tarefas que envolvem a geração de novos dados que se encaixam nos padrões dos dados de treinamento.
Alguns casos de uso comuns desses modelos são:
1. Geração de dados sintéticos
Para muitos modelos de visão computacional, é essencial ter um grande conjunto de dados de imagens de treinamento. Esses modelos precisam ser treinados em muitas variantes da mesma imagem ou recurso.
Tirar fotos do mesmo objeto de diferentes ângulos, fundos ou tons de cor nem sempre é realista. Muitos conjuntos de dados de imagens específicos de tarefas também tendem a ser limitados em tamanho porque sua criação requer habilidades específicas do domínio. Por exemplo, você precisa ter acesso a pneumologistas, laboratórios de radiologia e pacientes e hospitais que autorizem a criação de um conjunto de imagens de raios X de uma doença pulmonar específica.
Nesses casos, a opção mais pragmática é criar um conjunto de dados pequeno, mas altamente curado e relevante e, em seguida, gerar sinteticamente novos pontos de dados semelhantes ao conjunto de dados original.
2. Geração de imagens e textos
Geração de novas imagens a partir de uma descrição de texto ou geração de um novo texto a partir de um texto de entrada. A única classe de modelos que pode lidar com essas tarefas são os modelos generativos.
Os modelos de geração de imagens, como DALL-E, MidJourney e Stable Diffusion, são usados rotineiramente para gerar imagens que se adequam a uma descrição específica e não infringem os direitos autorais existentes.
Da mesma forma, os LLMs são frequentemente usados para gerar enredos de histórias fictícias, slogans e slogans de marketing, resumos de documentos e outros materiais semelhantes.
3. Modelagem de distribuições de probabilidade conjunta
Os modelos generativos são usados para tarefas baseadas na distribuição de probabilidade conjunta dos dados subjacentes. A modelagem da distribuição conjunta de retornos de ativos para prever o perfil de risco e retorno esperado de um portfólio de investimentos é padrão em finanças e gerenciamento de riscos.
Por exemplo, um gerente de investimentos pode querer saber a probabilidade de os preços de duas ações diferentes subirem ou caírem ao mesmo tempo - as PDFs conjuntas podem responder a essas perguntas.
O setor de serviços financeiros tem usado esses métodos estatísticos muito antes de o termo "modelos generativos" ser amplamente adotado.
4. Classificação não supervisionada
Problemas como a classificação não supervisionada são especialmente adequados aos modelos de mistura gaussiana. Nesses problemas, você tem uma ampla coleção de pontos de dados, mas não sabe a quantos ou a quais categorias os pontos de dados pertencem. É razoável esperar que os dados sejam provenientes de uma combinação de distribuições, que podem ser modeladas por um GMM.
Se o número e a lista de categorias fossem conhecidos antecipadamente, os métodos de discriminação teriam sido mais adequados.
Os GMMs também são úteis na análise de outliers (detecção de anomalias, detecção de fraudes etc.), em que os dados "usuais", como o comportamento de diferentes grupos de clientes, podem ser modelados como uma combinação de diferentes distribuições. Os pontos de dados anômalos são aqueles que diferem significativamente de qualquer um dos outros padrões.
5. Modelagem de sequência
Os problemas que envolvem sequências geralmente são resolvidos usando modelos ocultos de Markov. Um caso de uso cotidiano é a modelagem de sequências de genoma e re-sequenciamento.
Os HMMs também são usados no reconhecimento de fala, onde ajudam a prever a próxima sílaba com base na sequência de sílabas anteriores. A modelagem de sequências também é padrão para aplicativos de logística, como programações de entrega de pacotes. Da mesma forma, a transmissão e a propagação de doenças infecciosas geralmente são modeladas usando cadeias de Markov.
Quando usar modelos discriminativos
Matematicamente, os modelos discriminativos são usados para aplicações em que somente a probabilidade condicional é relevante, mas não a probabilidade conjunta. Assim, os modelos discriminativos são normalmente usados para problemas de classificação e de previsão.
Alguns exemplos são:
1. Problemas de classificação supervisionada
Problemas de classificação supervisionada, em que as classes (categorias) são conhecidas antecipadamente. Esse é o caso de uso essencial para KNNs e SVMs.
Você tem uma ampla coleção de pontos de dados, como dados de comportamento do cliente, incluindo padrões de gastos, valores de compra, frequência de compra, histórico de devoluções e assim por diante. Você precisa usar essas informações para classificar a lista de clientes em diferentes categorias, como clientes que gastam muito, caçadores de pechinchas, clientes regulares, clientes não sérios etc. Compare isso com os problemas de classificação não supervisionada, em que, conforme discutido anteriormente, os GMMs são comumente usados.
2. Tarefas preditivas
Em tarefas preditivas, como classificação e regressão, a prioridade geralmente é a velocidade e a precisão. Em princípio, os modelos generativos também são capazes de resolver esses problemas.
Em particular, os modelos generativos são preferidos quando há problemas como pontos de dados ausentes, quando apenas um conjunto de dados limitado está disponível para treinamento ou quando você espera adicionar novas categorias rotineiramente.
No entanto, para a maioria dos casos de uso padrão, os modelos generativos sofrem com taxas de erro mais altas e inferência mais lenta em tarefas preditivas porque seu cálculo envolve a distribuição de probabilidade conjunta. Portanto, para problemas de classificação e regressão padrão, em que um conjunto de dados grande e saudável está disponível para treinamento, os modelos discriminativos são a opção preferida devido às suas melhores características de desempenho.
3. Classificação com foco em resultados
Os modelos discriminatórios são preferidos para tarefas que se concentram apenas no resultado da classificação e não na modelagem dos dados subjacentes.
Por exemplo, se você quiser categorizar gravações de áudio em seus respectivos idiomas, não precisará de um modelo que entenda o idioma e a gramática. Um modelo de reconhecimento de fala seria um exagero para um problema de classificação. Basta que você se concentre no limite de decisão usando um modelo discriminativo. Portanto, você pode usar uma rede neural simples em vez de um LLM ou regressão logística em vez de um modelo bayesiano.
4. Tomada de decisões em várias etapas
As decisões em várias etapas, em que as etapas individuais envolvem escolhas não ambíguas, são boas candidatas para árvores de decisão. As árvores de decisão são frequentemente usadas como um filtro preliminar para selecionar pontos de dados que exigem uma análise mais profunda.
Por exemplo, considere a detecção de fraudes, geralmente resolvida com o uso de modelos complexos, como GMMs. Os seres humanos quase sempre investigam transações de alto risco, independentemente do modelo usado. Portanto, uma abordagem alternativa é usar uma árvore de decisão para sinalizar uma lista de transações potencialmente fraudulentas para investigação manual adicional.
As árvores de decisão também são usadas em muitas operações comerciais. O objetivo é decidir o curso de ação correto com base em condições predeterminadas. Essas tarefas não precisam de modelos generativos nem de modelos discriminativos mais complexos, como redes neurais.
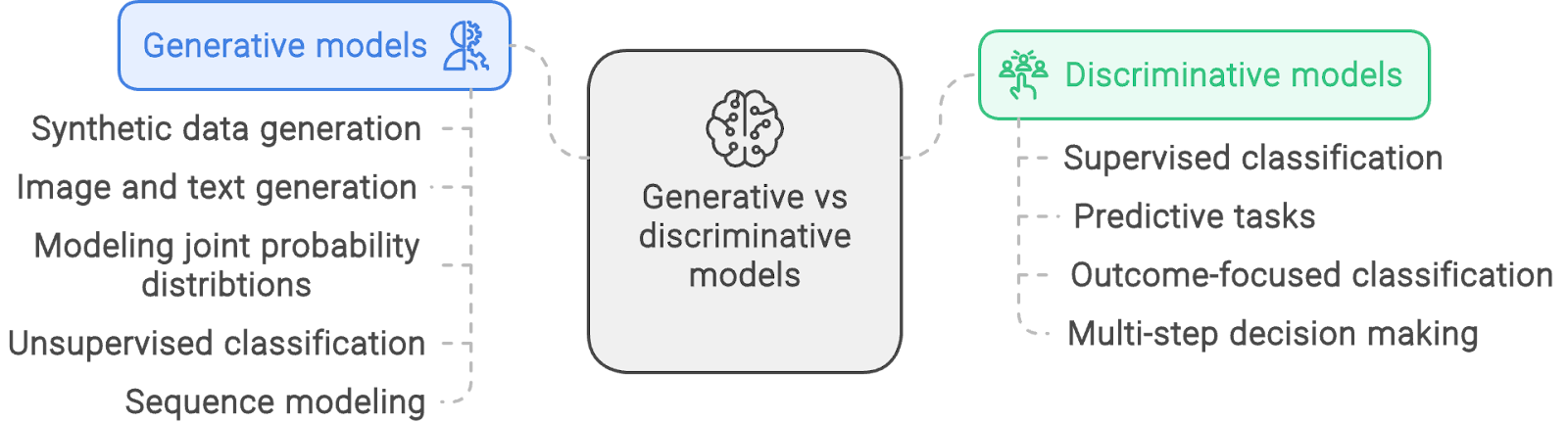
Exemplos de aplicações de modelos generativos vs. modelos discriminativos. Criado com napkin.ai
Conclusão
Este artigo explicou os princípios fundamentais e as principais diferenças entre os modelos generativos e discriminativos, as duas principais abordagens das técnicas de machine learning.
Embora a maior parte do machine learning seja baseada em métodos probabilísticos, os modelos generativos são baseados na distribuição de probabilidade conjunta, enquanto os modelos discriminativos usam apenas probabilidades condicionais. Assim, as duas classes de modelos têm aplicações e características de desempenho diferentes. Considerando a disponibilidade de uma ampla variedade de modelos, é essencial que você escolha a ferramenta certa para o trabalho.
Além de uma compreensão conceitual dos tipos de modelos e suas diferenças, é mais importante que você mesmo crie modelos. Comece com a postagem do blog que discute os métodos de treinamento supervisionado e a criação de um modelo simples de regressão logística.
Perguntas frequentes
Posso usar modelos generativos para tarefas de classificação?
Sim, os modelos generativos também podem ser usados para tarefas de classificação porque modelam a distribuição de probabilidade conjunta subjacente. Eles estimam as probabilidades condicionais (para tarefas de classificação) usando a regra de Bayes.
Também posso usar modelos discriminativos para tarefas generativas?
Não, para tarefas generativas, o modelo deve capturar a distribuição de probabilidade multivariada conjunta e as probabilidades marginais dos dados. Os modelos discriminativos capturam apenas a probabilidade condicional. Portanto, eles não podem ser usados para tarefas generativas.
Que tipo de modelo é correto para tarefas de classificação se o conjunto de dados de treinamento tiver dados ausentes ou incompletos?
É mais provável que os modelos discriminativos se ajustem excessivamente ao conjunto de dados. Assim, quaisquer deficiências no conjunto de dados se refletirão de forma mais proeminente nos parâmetros do modelo. É mais fácil para os modelos generativos compensar os pontos de dados ausentes porque eles modelam a distribuição dos dados subjacentes. Portanto, os modelos generativos são a melhor opção.
Quais modelos têm melhor desempenho nas tarefas de classificação?
Os cálculos subjacentes dos modelos discriminativos são mais simples. Assim, os modelos discriminativos têm melhor desempenho em tarefas de classificação.
Para uma tarefa generativa (ou discriminativa), posso escolher qualquer um dos modelos generativos (ou discriminativos)?
Em alguns casos, sim. Mas, em geral, não. Você precisa escolher um modelo cujos dados de treinamento e algoritmo se assemelhem aos seus dados e aos métodos que você deseja implementar.
Por exemplo, embora os modelos de Markov e os GANs sejam generativos, o primeiro é adequado exclusivamente para dados sequenciais. Os GANs têm um escopo mais amplo, embora tenham sido tradicionalmente usados para tarefas baseadas em imagens.
Da mesma forma, embora os modelos Naive Bayes sejam generativos, eles são usados principalmente para tarefas de classificação.
Estude os detalhes de cada modelo e os casos de uso típicos para determinar o que melhor se adapta ao seu problema.