Euler's Number (e) Explained: Its Significance and Applications

What do compound interest, logistic regression, and population growth models have in common? The answer is that they all rely on Euler’s number, or e.

Euler’s number is arguably one of the most important constants, second only to pi. It is used across disciplines from biology, physics, and astronomy, to data science, statistics, and financial analysis.

Fun fact: every lab I worked in used the first several digits of e or pi as a password somewhere within the lab. Why? Because everyone knew those numbers! That’s how often they are used.

So, let's explore what makes e so memorable, define its mathematical properties, and examine how it’s applied.

Introduction to Euler's Number

Euler’s number is a mathematical constant approximately equal to 2.71828. It is the base of the natural logarithm and a critical part of continuous growth and decay calculations. Similar to 𝜋, e is a universal constant. But while 𝜋 represents the ratio of a circle’s circumference to its diameter, e is a constant that naturally arises out of exponential processes. Euler’s number often appears when modeling processes that involve continuous change, for example, when calculating continuously compounded interest or modeling population growth.

Euler’s number is both irrational and transcendental. This means e cannot be expressed as a simple fraction or derived from solving any polynomial equation with rational coefficients. Its digits extend infinitely without repeating.

Historical Background

Let's look a bit at the history:

Jacob Bernoulli and the discovery of e

The story of Euler’s number begins in 1683, when Jacob Bernoulli studied the mathematics of compound interest. He asked a seemingly simple question: what happens if we compound interest continuously instead of annually?

To illustrate, consider an initial principal P invested at an annual interest rate r. If interest is compounded annually, the future value after one year is P(1 + r). If compounded semi-annually, it becomes P(1 + r/2)². As the number of compounding intervals (n) increases, the formula becomes P(1 + r/n)ⁿ.

The above graph shows the difference between annually compounded interest and continuously compounded interest. This is a rather extreme example of a $1000 principal with 50% yearly interest, in order to demonstrate the pattern.

Bernoulli discovered that as n approaches infinity, the value of (1 + 1/n)ⁿ converges to approximately 2.718. This constant, later named e, embodies the essence of continuous compounding.

Leonhard Euler: formalization and naming

Jacob Bernoulli may have discovered e’s presence in compound interest, but it was Leonhard Euler who fully developed the concept in the early 18th century. Between 1727 and 1731, Euler formalized the properties of e and gave it its now-familiar name.

Euler demonstrated that e could be represented as an infinite series:

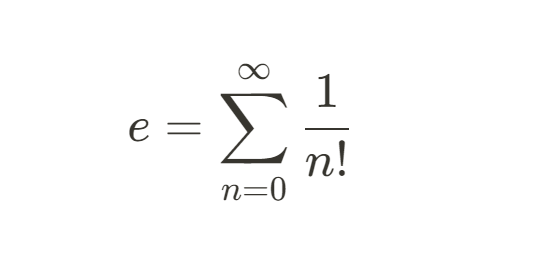
This series, derived from calculus, allowed e to be computed to any desired precision and opened the door to a deeper understanding of its properties.

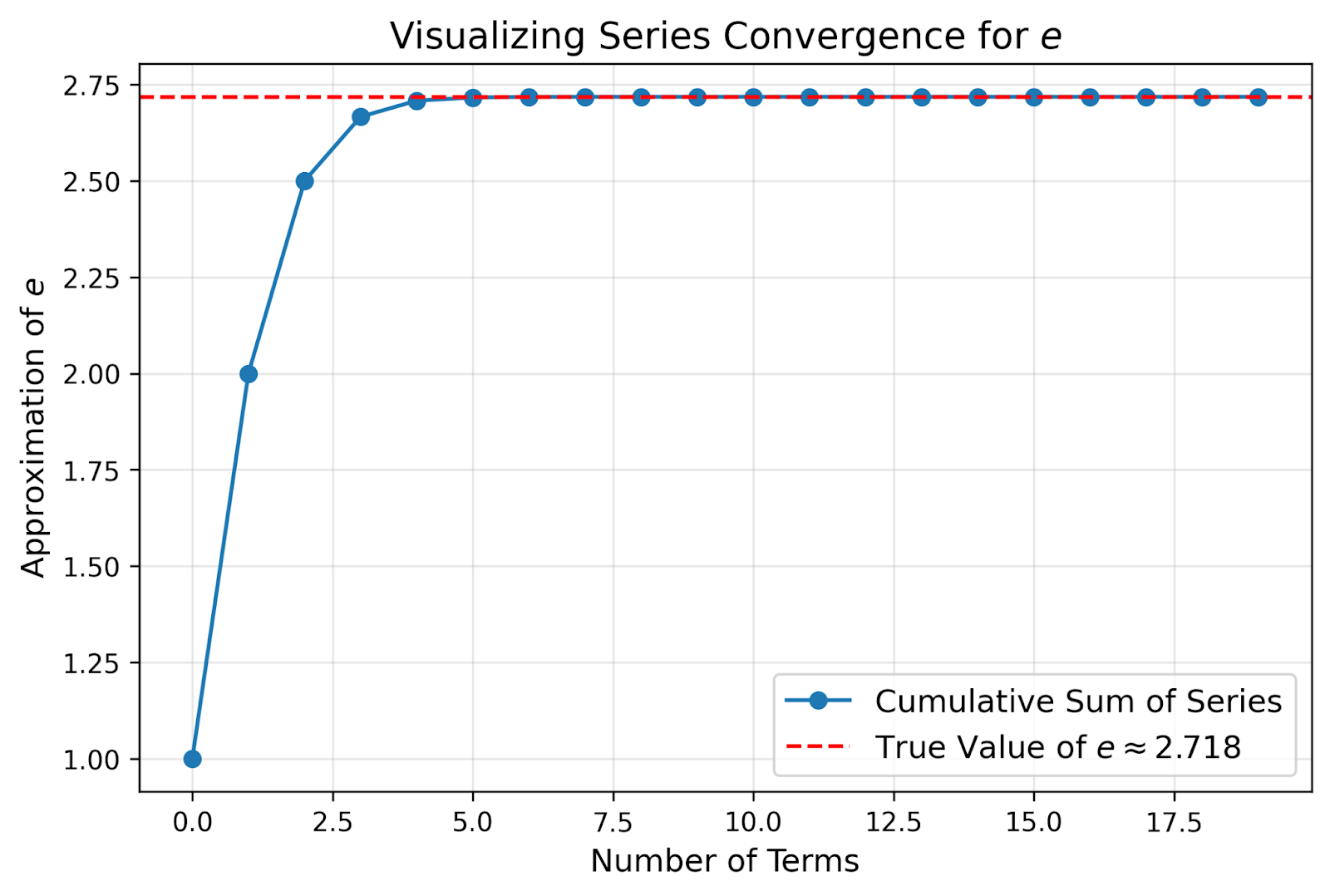
The above graphs shows how we can calculate e by adding up a series of numbers: e = 1 + 1/1! + 1/2! + 1/3! + …  The blue line shows the total as we add more terms, starting with just 1, then adding terms in the series. The red dashed line represents the actual value of e. You can see that the total gets very close to e after just a few terms, and each new term makes only a tiny difference. This is important because it shows that we can estimate e accurately without needing to add an infinite number of terms.

Evolution of e in mathematical literature

After Euler formalized e in the 18th century, its applications quickly expanded into a wide variety of fields. In the 19th century, its importance in solving differential equations became known. Mathematicians like Joseph Fourier used e in heat transfer equations, laying the foundation for the field of thermodynamics. Fourier's work on the diffusion of heat relied on exponential decay equations involving e, as detailed in The Analytical Theory of Heat.

By the 20th century, e had become a central tool in biology and population dynamics. The exponential growth model, P(t) = P0 ert, became widely used to describe population growth under ideal conditions. Similarly, in physics, e became useful for radioactive decay models, where the number of remaining particles follows N(t) = N0 e-𝝺t.

In more recent decades, e has found new relevance in computer science and machine learning. For instance, the sigmoid function, which is critical in neural networks, is defined by 𝝈(x) = 1/(1+e-x). This function maps inputs to outputs between 0 and 1, making it essential for classification tasks. Euler’s number also plays a role in the analysis of randomized algorithms and probabilistic models, as discussed in Deep Learning by Ian Goodfellow, et al.

Mathematical Properties of e

Now that we understand the history a bit, let’s explore some of its most important mathematical characteristics and definitions of Euler’s number.

ex with different values of x. Image by Author.

e as a limit

The definition of e as a limit is one of its most intuitive and historically significant representations. It arises naturally from the study of compound interest and is expressed as:

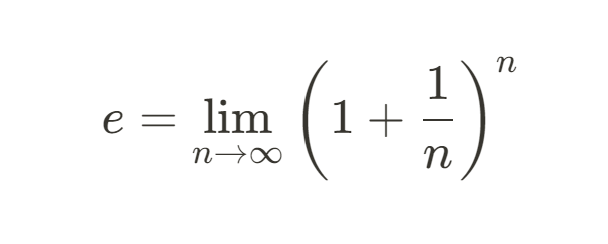
This formula defines e as the result of compounding growth infinitely. It is a conceptual foundation for understanding how e models continuous processes. This limit definition also shows us how e connects to exponential functions.

e as an infinite series

Another way to define e is through its infinite series representation:

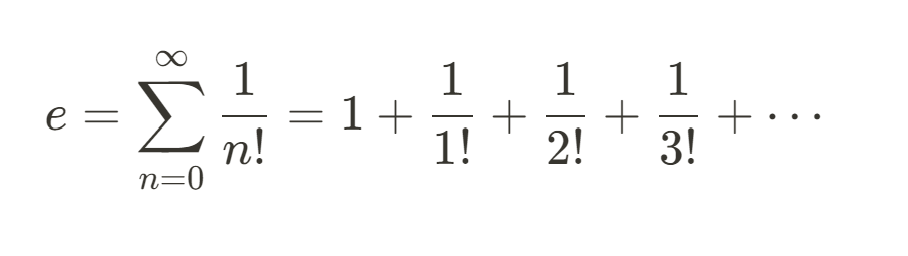
This series is derived from calculus and provides a precise way to compute e to any desired level of accuracy. It also highlights the connection between e and factorials, which frequently appear in probability theory and combinatorics.

The exponential function and calculus

The exponential function, where e is the base, is one of the most useful functions in mathematics, in my opinion. e^x is its own derivative:

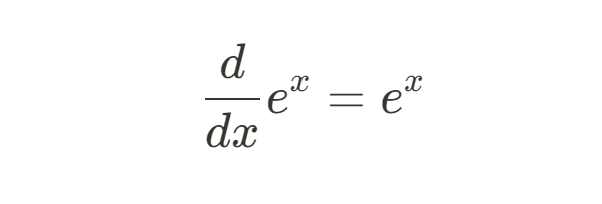
This means that the rate of change of e^x is always proportional to its current value. This property makes e^x the perfect mathematical tool for modeling continuous growth or decay. This property is what makes it useful in describing radioactive decay, population growth, and continuously compounded interest.

The natural logarithm

The natural logarithm, denoted as ln⁡(x), is the inverse of the exponential function e^x:

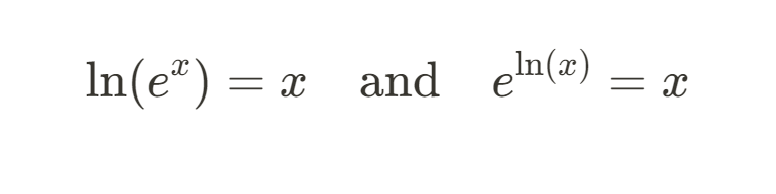
The natural logarithm is widely used in mathematics and statistics, particularly in transforming data.

Euler’s identity

Among us mathematical nerds, one of the more fun equations in mathematics is Euler’s identity:

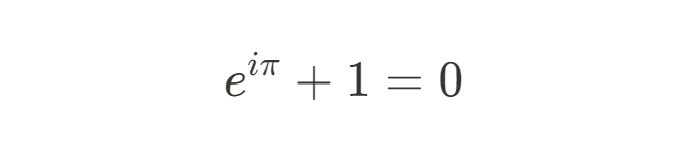
This equation is often regarded as the pinnacle of mathematical beauty because it connects five of the most fundamental constants in mathematics: e, i (the imaginary unit), 𝜋, 1, and 0. It also bridges seemingly unrelated areas of mathematics: exponential functions, complex numbers, and trigonometry.

e in probability and statistics

Euler’s number plays an important role in probability theory and statistics. For example, it appears in the formula for the Poisson distribution, which models the number of events occurring in a fixed interval:

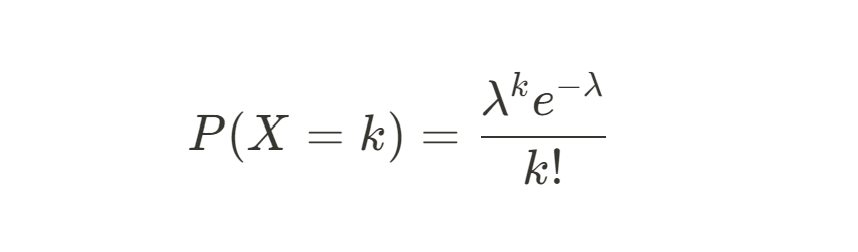
Here, e ensures that the probabilities sum to 1, making it indispensable in this widely used distribution.

Similarly, e is important for the exponential distribution, which models the time between events in a Poisson process:

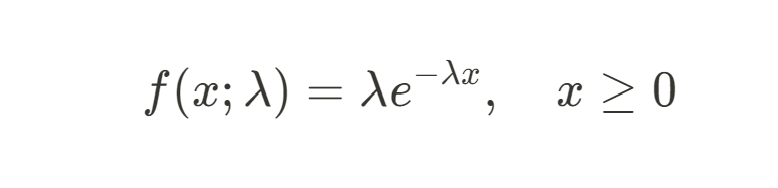
You can see that e also appears in the Gaussian distribution where it causes values farther from the mean to decrease exponentially.

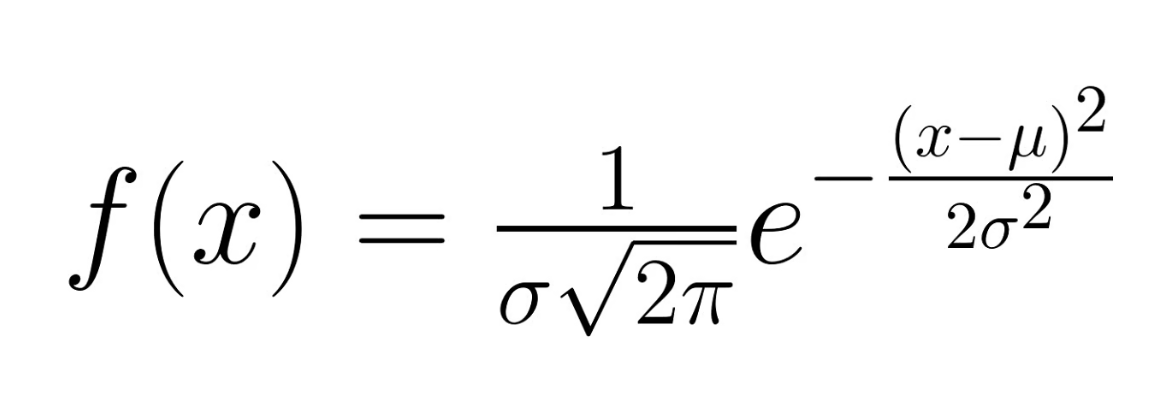
As you have seen, Euler’s number also connects seemingly unrelated areas of mathematics, from exponential growth to complex numbers, through equations like Euler’s identity. This interconnectedness demonstrates the deep and universal nature of e, making it one of the most important constants in mathematics. Without e, we would lack the mathematical tools to accurately model all kinds of processes that change smoothly over time.

Textbook Examples and Calculations

Let’s explore three textbook calculations that show how e can be applied.

Example 1: continuous vs. monthly compounding interest

Let’s consider a scenario where you invest $1,000 at an annual interest rate of 5%. We’ll calculate the future value of this investment after one year under two different compounding methods: monthly compounding and continuous compounding.

Monthly compounding

With monthly compounding, the interest is calculated and added to the principal each month. The formula for discrete compounding is

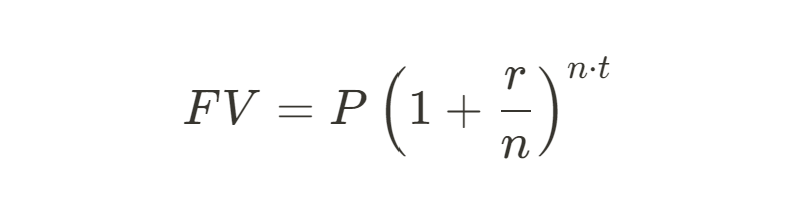
where P = 1000 is the initial principal, r = 0.05 is the annual interest rate, n = 12 is the number of compounding periods per year (in this case, monthly), and t = 1 is the number of years. Substituting these values into the formula gets us this:

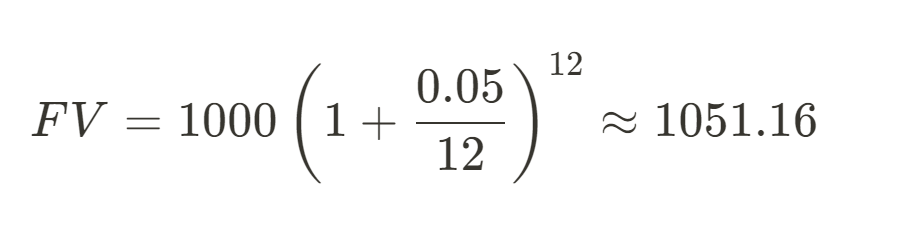
This calculation shows the future value of the investment when compounded monthly. In this case, after one year, the investment grows to approximately $1,051.16.

Continuous compounding

When interest is compounded continuously, it means that the interest is being added at every instant of time, creating a smoother growth curve. The formula for continuous compounding is:

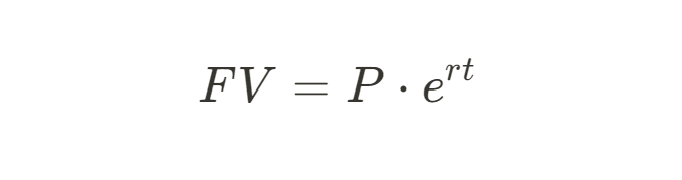
where P = 1000, r = 0.05, and t = 1. Substituting the values into the equation, we get this:

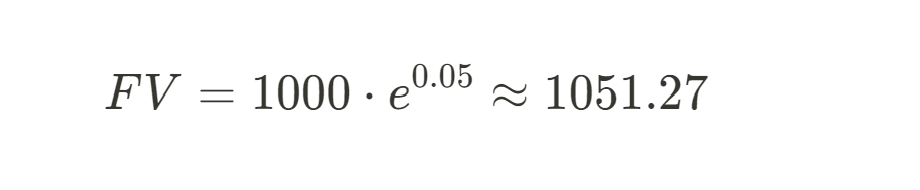
The value after one year in this case is $1,051.27. While the difference between the two methods may seem small after just one year, continuous compounding yields a slightly higher value. Over longer time periods or higher interest rates, the difference becomes much more significant.

The use of e here accounts for the fact that the interest is being compounded continuously, meaning it is growing at every instant, making the growth rate smoother.

Example 2: modeling population growth using e

Our second scenario comes from biology. Imagine a population of flies grows with a continuous birth rate of 20% per week and continuous death rate of 5% per week. If you start with 1,000 flies, how many will there be after 5 weeks? This problem is very similar to the compounding interest equation; in fact, you’ll notice that the equation is almost the same!

The continuous growth of a population can be modeled using this formula:

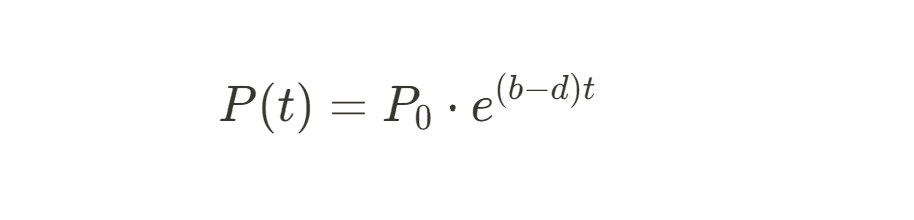
where P(t) is the population at time t, P0 is the initial population, b is the birth rate, d is the death rate, and (b-d) is the net growth rate. Substituting the values into the formula:

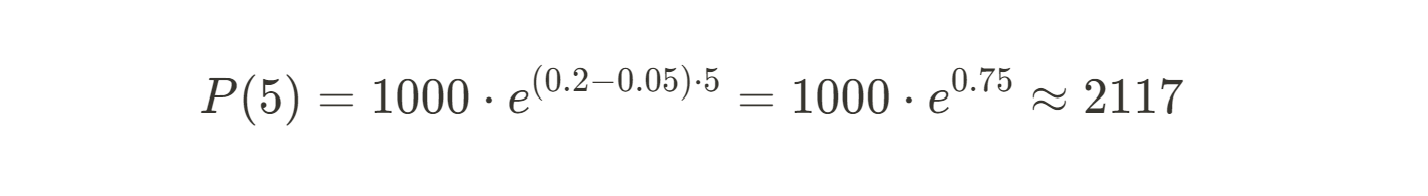After 5 weeks, the population will have grown to approximately 2,117 flies.

The role of e here is essential: it allows us to model continuous growth. Unlike discrete models that measure growth at fixed intervals, the continuous growth model with e accounts for the fact that growth happens at every moment in time, making it a more accurate representation of real-world processes like population growth, especially for large populations.

Example 3: probability scenarios involving e

Our third classic example comes from probability theory. Let’s explore the derangement problem, which asks: if you randomly assign n letters to n envelopes, what is the probability that none of the letters end up in their correct envelopes? This is known as a "derangement."

The probability of a derangement is given by the formula:

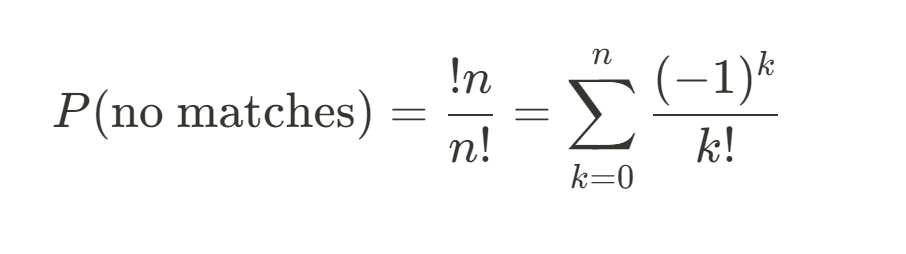
As n becomes very large, this probability approaches 1/e, or approximately 0.3679. This means that for a large number of letters, there is about a 37% chance that none of the letters will be placed correctly.

With 3 letters, there are 3!=6 possible arrangements. Of these, only 2 are derangements (where no letter is in its correct envelope). The probability is:

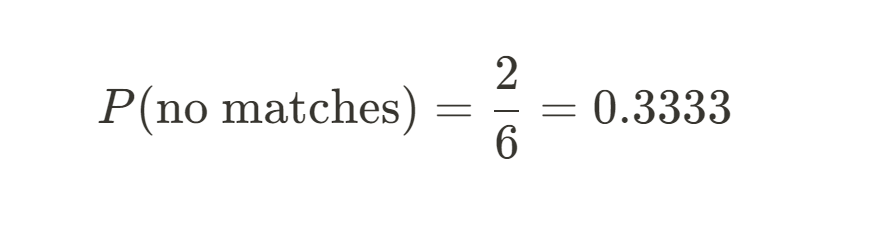
Let’s calculate the probability for 10 letters. Using the formula:

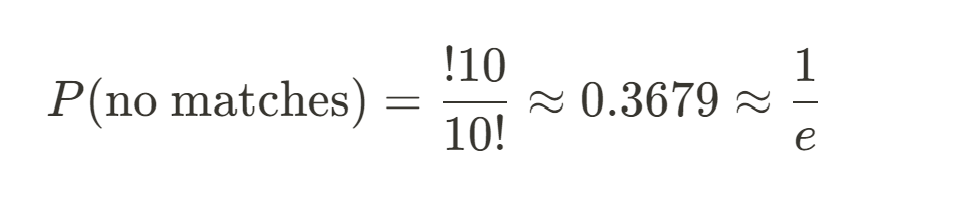
This result shows that even with as few as 10 letters, the probability of no matches is already very close to 1/e. As the number of letters increases, the probability converges on 1/e.

Euler’s Number in Professional Fields

Euler’s number appears in countless real-world applications. Its unique properties make it indispensable in fields ranging from calculus and biology to finance and engineering.

e in calculus

Euler’s number is fundamental in calculus, where it is central to understanding continuous change. As we’ve already mentioned, the exponential function e^x is unique because its derivative is itself:

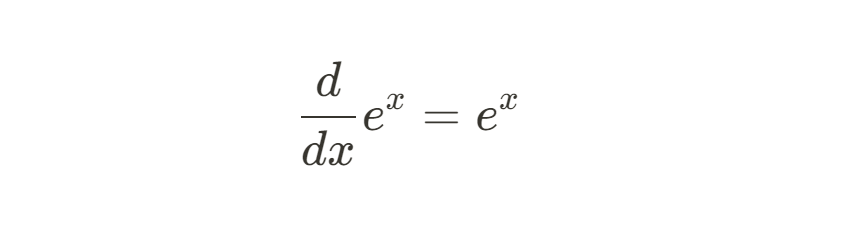
This property makes e^x essential for modeling processes where the rate of change is proportional to the current value. Euler’s number is involved in solving many differential equations.

e in biology and healthcare

My first introduction to e was in biology, where it’s used to model continuous growth and decay. For example, bacterial populations growing at a constant rate can be described by the classic population growth equation:

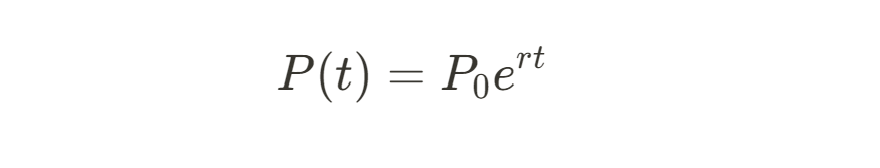
where P₀ is the initial population, r is the growth rate, and t is time.

Similarly, in healthcare, e is used to model drug metabolism, where the concentration of a drug in the body decreases exponentially over time:

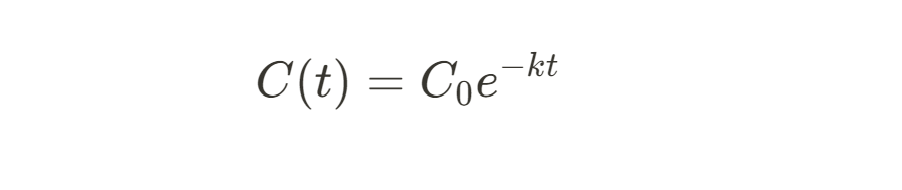
These models are vital for understanding biological processes and optimizing medical treatments, such as determining effective drug dosages or predicting bacterial growth in controlled environments.

e in engineering and physics

In engineering and physics, e is used to analyze systems that involve continuous change. For example, Euler’s formula:

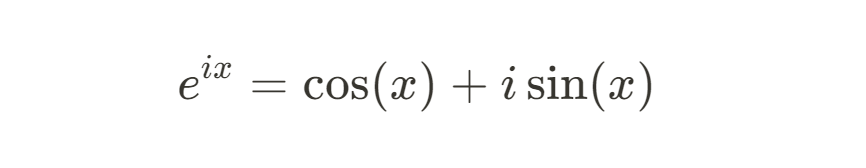
is used to represent sinusoidal waveforms in alternating current (AC) circuits. In signal processing, e is used in the Fourier transform, which breaks down complex signals into simpler frequency components. These applications are useful for fields like electrical engineering, quantum mechanics, and telecommunications.

e in finance

As you can imagine, Euler’s number is essential in finance, particularly in the calculation of continuously compounded interest, as we’ve already seen.

Euler’s number is also used in financial models like the Black-Scholes equation, which calculates the fair value of options by factoring in continuous asset price movements. By incorporating e, the Black-Scholes model accounts for the continuous nature of asset price movements, enabling precise pricing of options. You can learn more about financial modeling in our Financial Analysts in Google Sheets course.

e in computer science

In computer science, e is widely used in machine learning, cryptography, and simulations. The sigmoid function, a key component of neural networks, is defined as:

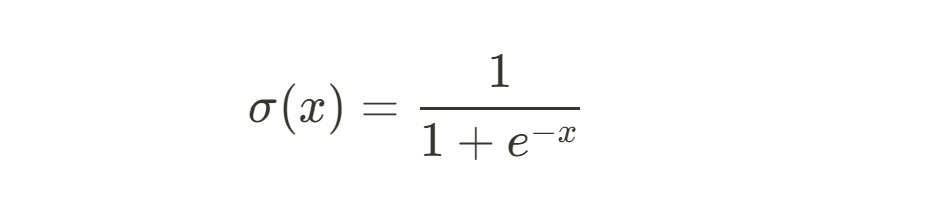
This function maps inputs to outputs between 0 and 1, making it useful for classification tasks. Euler’s number also appears in algorithms for simulating Poisson processes and exponential decay, which are used in random number generation, Monte Carlo simulations, and cryptographic systems.

e in insurance and demography

In actuarial science, e is used to model risks and calculate the future value of life insurance policies and annuities. For example, continuous interest accumulation is modeled using e^rt. In demography, e is used to describe population growth and mortality rates. The Gompertz function, which models aging and death rates, uses e to assess life expectancy.

e in geology

In geology, e is essential for modeling radioactive decay, as described by the equation:

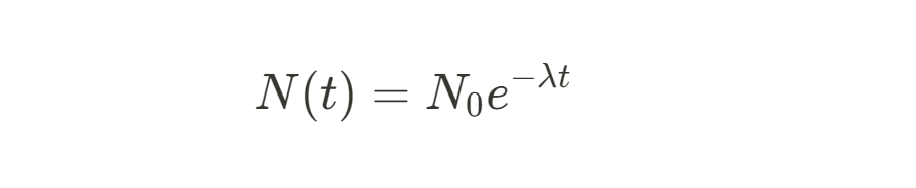
where N₀ is the initial quantity of a radioactive isotope, 𝝀 is the decay constant, and t is time. This equation is used for carbon dating, which helps determine the age of rocks and fossils. Euler’s number is also used in seismology to model the attenuation of seismic waves, which decay exponentially as they travel through the Earth. This aids in earthquake analysis and prediction.

e in meteorology

Meteorologists use e to model temperature changes and weather systems. For example, the cooling or heating of an object over time is described by:

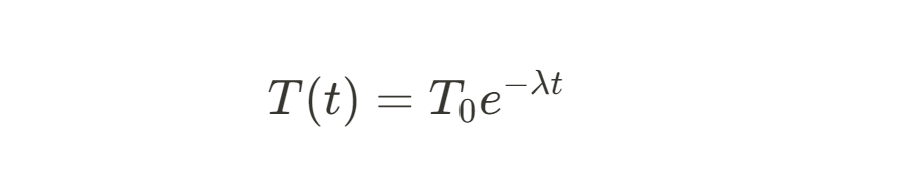
where T₀ is the initial temperature and 𝝀 is the rate constant. Exponential models involving e are also used in climate science to predict the long-term effects of carbon emissions and in weather forecasting to model the evolution of atmospheric pressure and cloud formation.

e in linguistics

Believe it or not, Euler’s number even has applications in linguistics! It is used in statistical models of word frequencies, such as Zipf’s law, which states that the frequency of a word is inversely proportional to its rank. This relationship can be modeled using exponential functions involving e.

In natural language processing (NLP), e is involved in algorithms like latent Dirichlet allocation (LDA), which models topic distributions in text. Exponential functions are also used to study linguistic evolution, tracking how languages change over time.

As you can see, Euler’s number is a universal constant used in a wide variety of diverse fields. Its applications are as infinite as its digits!

Misconceptions about e

As prevalent as e is, there are opportunities for confusion.

Euler’s number (e) versus Euler’s constant (γ)

It’s easy to mix up Euler’s number and Euler’s constant. After all, they both have Euler’s name attached to them. But they’re actually two completely different numbers, and they show up in different areas of math.

• e ≅ 2.718: This is the base of the natural logarithm. It’s super important in calculus, exponential growth, and anything involving continuous change. Think of e when you’re working with things like compound interest or population growth.
• γ ≅ 0.577: This is called the Euler-Mascheroni constant. It pops up in number theory and is related to the harmonic series (a fancy way of adding fractions like 1 + ½ + ⅓ +...). Think of γ when you’re working with problems involving the harmonic series or logarithmic growth.

Misuse in real-life applications

e shows up in a lot of different situations and can sometimes lead to confusion. It’s important to know when it’s appropriate to use e and when it’s not. For example, people often hear about continuous compounding and assume it’s always better than discrete interest. But many banks use monthly or quarterly compounding. So if you are trying to model real assets, you need to know whether continuous or discrete compounding is most appropriate, or you may find that your model doesn’t reflect reality.

Conclusion

Euler’s number, e, is one of the most widely-used constants in mathematics, second only to 𝜋. It’s a tool that simplifies complex calculations, models growth, and makes it possible to model continuous change. You can learn to use e in your coding in our Exponents in Python tutorial. If you’re interested in learning more mathematics, check out our Introductory Statistics or Linear Algebra courses.